基于粒子群算法的新安江模型参数的优化
温海燕
(河北省唐秦水文水资源勘测局,河北 唐山 063000)
正确的来水量预报是防汛抗旱和水利水电工程设计、施工、调度、管理等的重要依据。水文预报模型具有操作简单、计算速度快的特点,通常能在很短的时间内得到较为准确的结果。特别是伴随着计算机技术的飞速发展,水文预报模型日益普及。但运用水文模型预报的精度如何,则很大程度上取决于模型的参数,因此,参数优化非常重要。
1 基本资料
选定滦河流域唐秦地区大黑汀水库(滦河干流)、桃林口水库(一级支流青龙河)至滦县水文站(滦河出口控制站)区间为研究区域,流域面积3550 km2。根据研究区域现有观测站网自测报系统站网规划,将研究区按照泰森多边形法则划分为 13个流域单元,分别为七道河、上营、迁西、东荒峪、太平寨、肖家营子、冷口、桑园、迁安、夏官营、桃林口、卢龙和滦县。分别统计研究区域1979~2002年历年用水量资料、各单元逐日降水量资料、滦县站蒸发量资料及大黑汀水库、桃林口水库出库和滦县水文站年径流量系列,作为进行模型参数优化的基本资料。
2 模型选择
研究区域地处华北平原滦河流域的燕山迎风区,大部分地区呈半湿润、半干旱状态,故预报模型选择目前广泛应用于水文预报工作,适用于半湿润半干旱地区的新安江模型[1],[2]。新安江模型主要包含以下参数[3],[4],[5]:
1)蒸散发参数K,WUM,WLM,C;K为蒸散发能力和蒸发皿实测值之比;WUM为上层土壤水容量,对蒸散发计算影响显著;WLM为下层土壤水容量,常取60~90 mm;C为深层蒸散发系数,与流域上深根植物的覆盖面积比例有关。
2)产流参数IM,W M,B,FC,KF,BF,KG,KI;IM为不透水面积比例;WM为张力水容量,分为上层、下层与深层3层,分别为WUM,WLM,WDM;B为张力水蓄水容量曲线的方次,与流域面积有关;FC为稳定下 渗率,唯一地取决于水力传导度k;F为渗透系数,反映土壤含水量对下渗的影响;BF为反映流域上下渗率分布的不均匀性。
3 粒子群算法
粒子群优化算法(Particle Swarm Optimization,PSO)是由 Kennedy和 Eberhart于 1995年提出的一种模拟生物群落行为的进化算法[6]。该算法本质上是一种多代理算法,是一种基于迭代的优化工具,近年来广泛应用于函数优化、车间调度等问题[7]。
3.1 PSO的基本原理
假设在一个D维的目标搜索空间中,有m个粒子组成一个群落,其中第i个粒子表示为一个D维向量=(xi1,xi2,…,xiD),i=1,2,…,m,第i个粒子的“飞翔”速度也是一个D维向量,记为(vi1,vi2,…,viD)。每个粒子都有一个由被优化的函数决定的适应值(Fitness Value),并且知道自己到目前为止发现的最好位置(pbest)和现在的位置每个粒子的位置就是一个潜在的解。将?代入一个目标函数就可以计算出适应值,根据适应值的大小衡量?的优劣。这个可以看作是粒子自己的飞行经验。除此之外,每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest是在 pbest中的最好值)。这个可以看作是粒子同伴的经验。每个粒子使用下列信息改变自己的当前位置:1)当前位置;2)当前速度;3)当前位置与自己最好位置之间的距离;4)当前位置与群体最好位置之间的距离。
PSO是一种基于迭代的优化工具。对于第k次迭代,每个粒子的变化:
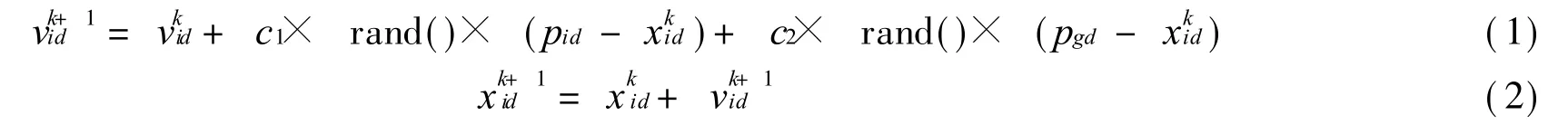
式中,i=1,2,…,m,m是该群体中粒子的总数;vkid 为第k次迭代粒子i飞行速度矢量的第d维分量;xkid为第k次迭代粒子i位置矢量的第d维分量;pid为粒子i个体最好位置pbest的第d维分量;pgd为群体最好位置gbest的第d维分量;c1,c2为权重因子;rand()为随机函数,产生 [0,1]的随机数。
3.2 引入惯性权重w的粒子群算法计算原理
式(1)是根据粒子以前的速度和粒子现在位置与自己曾经最好的位置之间的距离及当前位置和群体最好位置之间的距离三者的和,来计算粒子新的速度。Shi与Eberhart的研究发现,式(1)的第一部分vid由于具有随机性且其本身缺乏记忆能力,有扩大搜索空间、探索新的搜索区域的趋势。因此,具有全局优化的能力。在考虑实际优化问题时,往往希望先采用全局搜索,使搜索空间快速收敛于某一区域,然后采用局部精细搜索以获得高精度的解。
对PSO全局和局部之搜索能力的平衡主要被惯性权重控制[8],因此,在式(1)的vid前乘以惯性权重w,用来控制粒子以前速度对当前速度的影响,它将影响粒子的全局和局部搜索能力,即

w较大则算法具有较强的全局搜索能力,w较小则算法倾向于局部搜索。选择一个合适的w可以平衡全局和局部搜索能力,这样可以以最少的迭代次数找到最优解。
3.3 PSO算法求解最优化问题
此处将以图形的方式说明PSO算法求解最优化问题。对一个最优化问题而言,就是要找到全局最小(或最大)点。如图1所示,为某一二维空间中最小化问题,全局最优解点在o处。图中标明了第i个粒子从位置i1更新到位置i2的过程。其中v1是此时刻全局极值gbest引起的第i个粒子向gbest方向的速度;v2是此时刻第i个粒子的个体极值pbesti引起的第i个粒子向pbesti方向的速度;v3是此时刻第i个粒子自身具有的速度。在速度v1,v2,v3的共同作用下,最终粒子将以速度v到达新的位置i2。下一时刻,粒子i将从i2位置出发,以同样的方式向最优点o靠近。如此迭代,所有粒子都将逐步向最优点靠近,最终找到最优点。
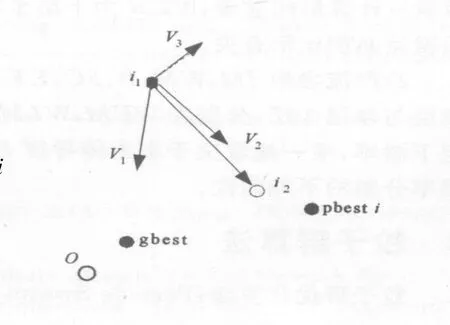
图1 PSO算法求解最优问题过程示意图
4 粒子群算法优化垂直混合产流模型参数
4.1 优选参数的确定
选出模型中 8个敏感参数,通过粒子群算法对其进行优选。优选参数的物理意义及取值范围见表 1。

表1 优选参数的物理意义及取值范围
4.2 基于粒子群优化算法的新安江模型参数的优化
4.2.1 目标函数
利用日模型优化参数时,其目标函数为

式中,Q(i)为历年实测年径流量,Q′(i)为历年模拟年径流量。
4.2.2 粒子群算法参数优化步骤
步骤1:初始化粒子,将种群中的每一个粒子随机地分布在空间中;随机地给每个粒子一个初始的速度vi,根据表 1中给出的各参数的范围,得出每个参数的vmax,vi∈ (-vmax,vmax);根据每个粒子,调用新安江模型,计算各年径流量,按式(4)计算目标函数值,并将各粒子计算出的目标函数值设为其相应的个体极值pbest(即个体极值点的适应度值),从个体极值中选出一个最好的作为全局极值gbest(即全局极值点的适应度值),并将gbest设置为该最好粒子的当前位置;给定学习因子c1和c2。
步骤2:根据迭代次数计算惯性权重w,通过式(3)计算粒子的速度,判断速度vi是否超出其取值范围(-vmax,vmax),若超出范围,则将其设为边界值。
步骤3:根据粒子速度vi和式(2)计算粒子的位置,若粒子的任何一维超出范围,则返回到步骤 2,依靠随机数重新计算粒子的速度和位置,直至粒子满足范围要求。
步骤4:对每个粒子,根据其在解空间的位置,调用垂直混合产流模型,进行预报,通过式(4)计算目标函数值,作为其适应度。
步骤5:对每个粒子,比较其适应度值和粒子所经历过的最优解pbest,若前者优于后者,则用当前值更新粒子记忆的pbest;否则,保持pbest不变。
步骤6:比较当前群体最优解和gbest标识的粒子所找到的最优解,若前者优于后者,则更新gbest;否则,保持gbest不变。
步骤 7:当结束条件(如达到最大迭代次数 )满足时,退出计算,否则返回到步骤 2。
4.3 计算成果及分析
4.3.1 计算成果
选用滦河流域总出口断面控制站滦县水文站1979~2002年实测年径流量资料,采用人工试错法和粒子群算法率定模型参数。本次率定粒子个数分别采用了10个和 20个,迭代次数分别采用了 50次、100次、200次和400次。计算结果显示,不管是10个粒子还是 20个粒子,当迭代次数增加到 400次时,其目标函数值不再变化,因此认定迭代 200次时,已经达到最优。参数最终率定成果见表 2,年径流模拟成果见表3。

表2 1979~2002年径流参数优化结果

表3 1979~2002年径流量模拟结果
4.3.2 成果分析
从表3可以看出,用 PSO算法进行模型参数率定,并运用此参数值对年径流量进行模拟,其绝对误差和相对误差均比人工试错法低。若以模拟年径流量与实测径流量相对误差在±20%内为合格,则人工试错法合格率为 41.7%,PSO算法的合格率为 58.3%,精度较人工试错法有所提高。
若以1979~2002年平均径流量为界,将这24年分为大水年和小水年,则大水年 PSO优化和人工试错法模拟径流量的合格率分别为 80%和70%;小水年 PSO优化和人工试错法模拟径流量的合格率分别为37.5%和 18.8%。可见,利用 PSO优化计算结果明显优于传统的人工试错法。
5 结束语
粒子群算法是一种全新的优化算法,文中采用滦河流域大黑汀—桃林口—滦县区间长系列的降水、流量等实际资料,对区间新安江预报模型的参数进行了优化,并比较了传统的人工试错法和粒子群算法对区间年径流量的模拟成果。从结果可以看出,粒子群算法优化参数具有模拟精度高、调算速度快的特点,肯定了该算法在新安江模型参数优化中的适应性。
[1]包为民,张建云.水文预报 [M].第 4版.北京:中国水利水电出版社,2009.
[2]芮孝芳.产汇流理论 [M].北京:水利电力出版社,1995.
[3]王佩兰,赵人俊.新安江模型(三水源)参数的客观优选方法 [J].河海大学学报,1989,17(4):65-68.
[4]赵人俊,王佩兰,胡凤彬.新安江模型的根据及模型参数与自然条件的关系 [J].河海大学学报,1992,20(1):52-59.
[5]杨小辉,郭菲菲.率定新安江模型(三水源)产汇流参数 [J].贵州水力发电,2000,14(1):7-10.
[6]Kennedy,J.and Eberhart,R.Particle Swarm Optimization[C].//IEEE International Conference on Neural Networks(Perth,Australia),IEEE Service Center,Piscataway,N J,1995,IV:1942-1948.
[7]张利彪,周春光,刘小华,等.粒子群算法在求解优化问题中的应用 [J].吉林大学学报,2005,23(4):385-389.
[8]郭文忠,陈国龙.粒子群优化算法的研究进展 [J].福建电脑,2005(4):7-8.

