桥梁桩基抗震设计的六弹簧模拟方法

涂金平 刘延芳

1 概述

在桩基结构地震反应分析中，桩—土—结构的相互作用问题一直是个难点。地基与结构的动力相互作用可以分为运动学相互作用和惯性相互作用。由于桩—土—结构的相互作用是一个复杂的耦合的相互作用过程，是一个涉及多学科的交叉性研究课题。几十年来，国内外许多学者进行了大量的研究，提出了许多模型和方法，但由于土这种介质的复杂性，桩—土—结构的相互作用问题至今没有得到较好的解决［1］。本文以一工程实例为背景，使用反应谱分析方法对于目前桥梁桩基常用的六弹簧模型模拟方法进行比较研究，着重说明其在地震反应分析中存在的方向组合问题。

2 理论基础

从反应谱的定义可知，地震反应谱给出的是单自由度体系在一定阻尼的情况下线性地震反应的各种最大值，而不计最大值的发生时间。

通过振型分解法可以将多自由度体系的线性振动方程分解为多个相互独立的单自由度体系的振动方程。因此，在多分量地震动的作用下，应用反应谱方法计算结构的地震反应应涉及到两个组合问题。其一是在每一个分量下的振型组合问题;其二是在不同地震动分量引起的结构地震反应的方向组合问题［1，2］。

本文考虑的是两个方向的地震动输入，即水平纵向+竖向与水平横向+竖向输入。最不利桩基顶部的轴力是由承台底地震反应的三个独立分量(轴力(N)、剪力(Q)、弯矩(M))共同作用产生的。由于通过有限元计算所得的承台底六弹簧的响应中已经包括了SRSS的方向组合问题，所以此处对于桩基内力计算而言只是一个近似的SRSS方向组合，即认为承台底的轴力主要由竖向地震作用产生，而剪力与弯矩主要由水平向的地震作用产生。

因而采用式(1)～式(3)的SRSS组合方式进行桩基内力的计算:

单桩轴力为:

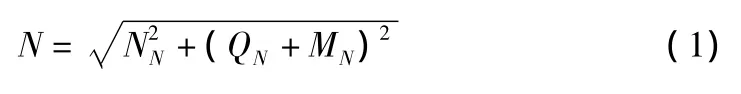
单桩剪力为:

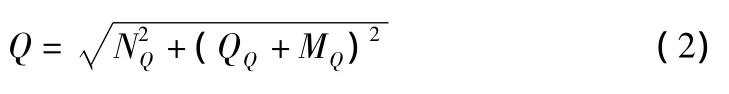
单桩弯矩为:

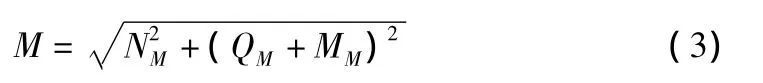
其中，NN，QN，MN分别为承台底轴力、剪力、弯矩单独作用下单桩的轴力，其余表示相似。

3 计算模型及地震动输入

本文以如图1所示的承台为例，图1为某桥主塔下的桩基承台的平面图。主塔基础采用钻孔灌注桩方案。承台为哑铃形，平面尺寸85.4 m ×37 m，厚10 m。桩基为42根 D3.0 m ～D2.7 m钻孔桩，采用行列式布置，按照摩擦端承桩设计，考虑钢护筒与桩基础共同受力。

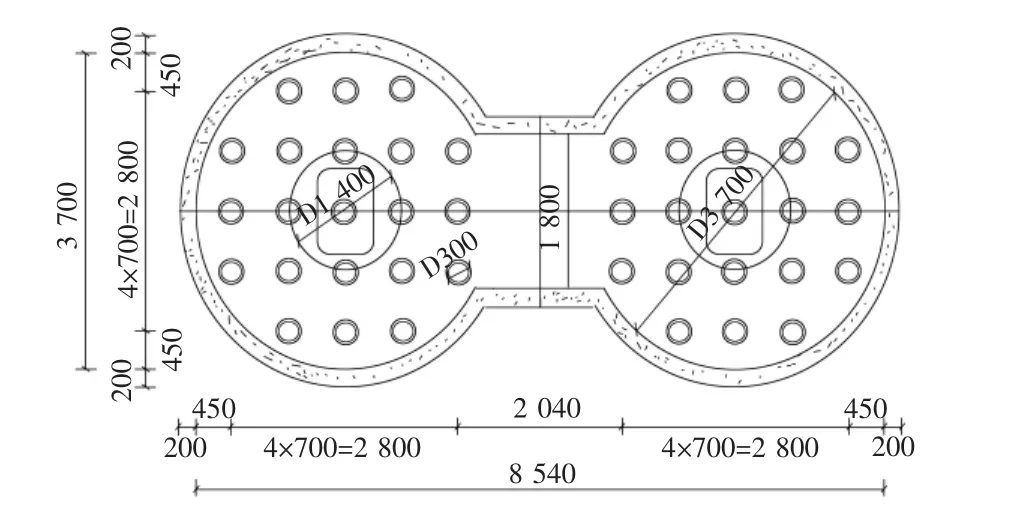
图1 桩基承台示意图

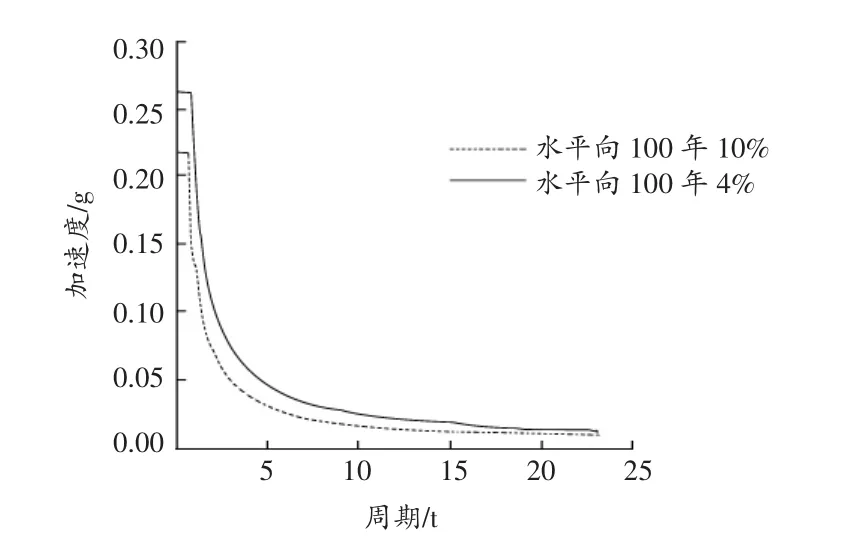
图2 水平向地震动输入

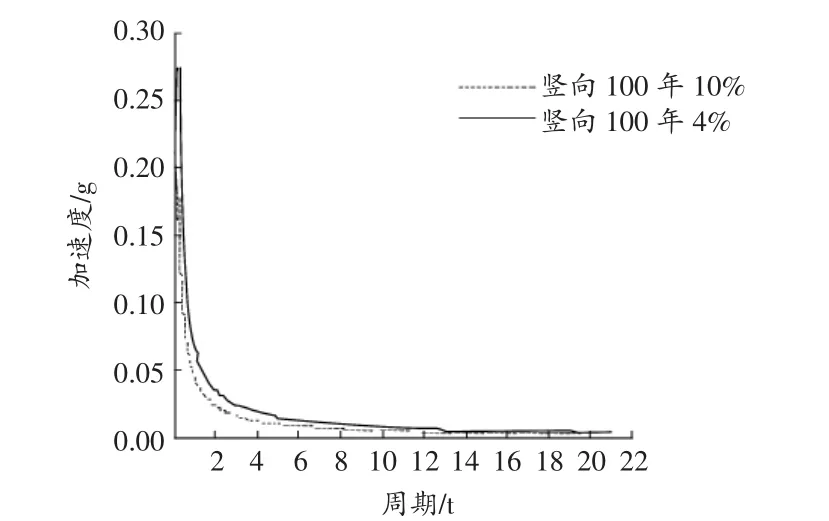
图3 竖向地震动输入

采用SAP2000有限元软件，建立实例的桩基六弹簧模型与弹性嵌固模型，采用反应谱分析方法，水平、竖向地震动输入见图2，图3，阻尼比取为5%。

4 计算结果及分析

表1列出了六弹簧模型承台底的地震反力。通过得到的承台底的地震响应，采用m法反算计算可以得到各桩基的反力。表2列出了六弹簧模型通过承台底反力反算得到的最不利桩基桩顶内力与弹性嵌固模型所得到的最不利桩基桩顶内力的比较值。

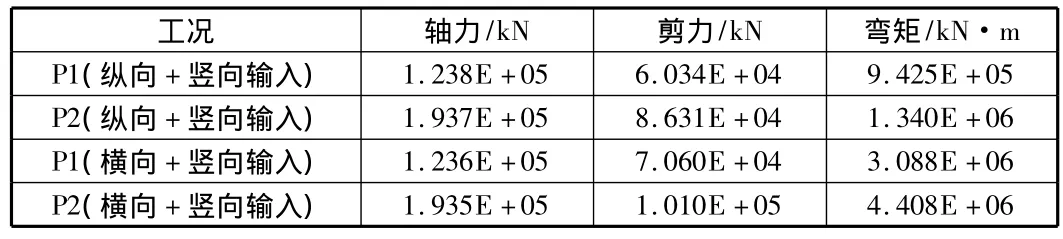
表1 两概率水平下六弹簧模型承台底地震反力

表2 两概率水平下六弹簧模型与弹性嵌固模型最不利单桩地震反力比较

由表2可以看出，六弹簧模型所计算得到的最不利单桩的剪力、弯矩与弹性嵌固模型所得到的最不利单桩的剪力、弯矩差别不大，剪力的最大误差为5.64%、弯矩最大误差为8.03%，均为实际工程可接受的误差范围。但是与剪力、弯矩不同，两种计算模型的轴力的误差则较大，最小的误差也有40.5%，大大超过了工程所能接受的范围。而对于桥梁桩基而言，轴力是其控制设计的关键力学参数。本文将六弹簧所得到的承台底的地震响应单独作用在承台底，进行单桩的内力计算。并将计算后的结果按照式(1)～式(3)的组合方式进行组合，得到最不利桩基的计算结果与弹性嵌固模型的计算结果进行了比较，结果如表3所示。

表3 六弹簧模型SRSS组合与弹性嵌固模型最不利单桩桩顶地震反力比较

通过表3可以看出，经过SRSS组合所得到的结果与弹性嵌固模型计算所得的结果误差均在实际工程中可以接受的范围内。

由于规范所规定的m法中的m值是基于土体的小变形和静力条件给出的，因此在计算结构的地震动力响应时，没考虑桩身自身的地震惯性力，因此结果偏小。所以正如孙利民教授［7］所建议的，工程技术人员进行抗震设计与分析时，有必要根据地震波的类型、大小恰当的选取m值，来计算等效土弹簧刚度，以期与实际地震作用时的情况相符。

5 结语

本文以一工程实例为背景，研究了抗震分析时采用的六弹簧模型在求解桩基反力时存在的方向组合的问题。由于m法是基于静力条件给出的，因此采用m法计算所得的单桩桩顶最不利内力是承台底各项反应单独作用下所得的计算结果的代数叠加。对于静力计算而言，各项反力的计算结果的叠加是合理的。但是对于结构的地震反应而言，各项反力的计算结果简单的代数叠加是不合理的。将六弹簧模型所得承台底内力，通过m法得到的各项反应单独作用下的单桩桩顶的内力，经过SRSS组合所得到的结果与弹性嵌固模型计算所得的结果误差均在实际工程中可以接受的范围内，以本文为例，轴力最大误差也仅为15%左右。

［1］ 范立础.桥梁抗震［M］.上海:同济大学出版社，1997.

［2］ 杨昌众.桩基桥梁的场地判别和地震反应计算的实用简化方法［D］.上海:同济大学桥梁工程系，1987.

［3］ 叶爱君.苏通大桥抗震性能最终研究报告［R］.上海:同济大学土木工程防灾国家重点实验室，2004.

［4］ Penzien J，Scheffey C F，Parmelee R A.Seismic analysis of bridges on long piles［J］.ASCE，1964，90(EM3):223-254.

［5］ 范立础，胡世德，叶爱君.大跨度桥梁抗震设计［M］.北京:人民交通出版社，2001.

［6］ 范立础，王志强.桥梁减隔震设计［M］.北京:人民交通出版社，2001.

［7］ 孙利民，刘 东，潘 龙.桩—土相互作用集中质量模型的土弹簧刚度计算方法［A］.中国土木工程学会桥梁及结构工程学会第十四届年会论文集［C］.2000.

［8］ 刘冠营，韦景宁.溶洞群地区桥梁桩基设计与施工中的若干问题［J］.山西建筑，2011，37(9):177-178.

［9］ 谢华伟，雷叙渌.桥梁结构震害及抗震设计理念浅议［J］.山西建筑，2010，36(18):303-304.