基于暂态能量函数线性规划法的切负荷算法

徐 茜，孙裕佳

（山东青岛供电公司，山东 青岛 266002））

0 引言

随着电力行业的发展，电能经济传输、电力系统的安全评定等已成为重要的研究课题。输电线路作为电能传输的重要设备，对其在安全运行中的负荷极限的研究就显得尤为重要。如果得到尽可能多的关于电力系统在安全运行状态下所能承受的极限参数值，那么就可以更好的保证电力系统的安全运行。电力系统安全性评估可以表示出一个重大突发事故的不稳定性，操作人员如果知道了安全运行的极限参数，知道应该如何采取诸如切负荷的措施，那么系统的安全运行就有了保证。因此本文研究了系统暂态稳定情况下特定支路的潮流极限，并进一步计算出了需要切除的负荷量来维持系统的安全运行。

近些年来，有很多运用暂态能量函数法对电力系统暂态稳定性进行评估的研究。经过长期的发展和改进，暂态能量函数法已经较为成熟，这为暂态能量函数法应用在电力系统暂态稳定的可靠性和安全性评估的研究中奠定了基础。

暂态能量函数法相对于传统的暂态稳定分析有两点显著优势。第一，暂态能量函数法避免了耗费时间的逐步仿真；另外一方面，暂态能量函数法的“能量裕度”可以表征系统稳定或不稳定程度。对于一个给定的扰动，如果能量裕度是正值，则系统是稳定的；如果能量裕度是负值，则系统是不稳定的。

为了便于暂态稳定分析在实时变化的运行条件下进行快速计算，文献［1］提出了暂态能量函数灵敏度方法。利用暂态能量裕度对发电机出力变化值的灵敏度，可以快速分析发电机出力变化时的系统暂态稳定情况，这些灵敏度值对于稳定极限的计算至关重要。在运行中，稳定极限通常以重要的接口流极限的形式来定义。结合暂态能量裕度的灵敏度分析和潮流分布因子来快速计算线路潮流极限。用时域仿真方法，需要通过试凑法进行计算，将涉及多次暂态稳定计算。运用线性规划理论，将本文中的暂态能量函数进行线性化，可以快速计算出线路潮流极限和切负荷量。

1 算法原理

本文在构造暂态能量函数法时采用经典电力系统模型。电力系统经典模型中发电机用d轴暂态电抗后的恒定电势代表，负载用恒定阻抗表示以及将电力网络收缩到发电机内节点。这类模型最简单，数据最少，在计算速度上有明显优势，适于大规模电力系统的暂态稳定分析。

对于一个特定的支路潮流变化量，ΔIl，需要知道由这个新的支路潮流引起的能量裕度的改变量：

其中，能量裕度的实际变化量是由造成支路潮流变化的发电机切机组合所决定的。

假设，系统所有参数的微量变化都可以线性化。首先，将能量裕度对多台发电机负荷变化的行为作线性化处理。如果能量裕度如此线性化，则能量裕度的变化量可描述为：

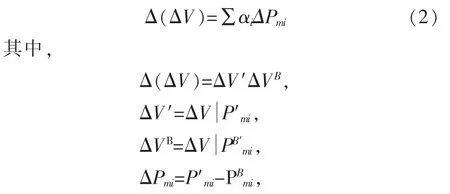
P′mi为发电机i甩负荷后有功出力，为发电机i的基荷。αi为能量裕度对发电机i出力变化量的灵敏度。

另外，支路潮流的变化也进行关于发电机出力变化的线性化处理，方程描述为：

其中，sli为潮流分布因子，可以由潮流计算得来。

暂态稳定约束下的支路潮流极限问题描述为下列方程：

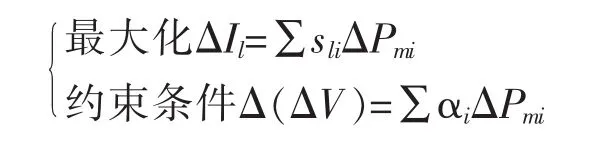
在实际运行中，发电机还要满足热稳定极限的要求，即：

这样，每台发电机可切负荷量就要满足一定的约束条件。定义：

其中第n台发电机为被调整的发电机。为了简化问题，做如下假设：

1）临界发电机的出力改变不会影响系统的故障模式。如果故障模式改变，意味着超前机组的组合发生了改变，并且不稳定平衡点也发生了变化。因此，基本状态下的不稳定平衡点就不能用作计算故障后不稳定平衡点的初始值。假设故障模式不改变，则基本情况下的不稳定平衡点可以作为计算故障后不稳定平衡点的初始值。

2）系统总发电量保持恒定。也就是某发电机出力的变化伴随着一种大小相等方向相反的参考机出力的变化。

3）所有的ΔPmi正负号相同。即如果基本状态下的能量裕度表明系统稳定，则临界机组均增加负荷降低能量裕度；如果基本状态下的能量裕度表明系统不稳定，则临界机组均减少负荷来提高能量裕度。

4）所有的αi都是负值。也就是说，临界机组负荷增长（减少），则能量裕度减小（增大），也就导致系统的稳定程度减少（增加）。

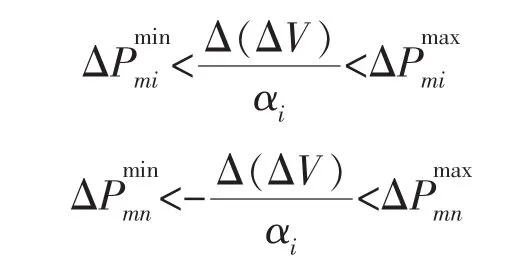
5）发电机的热稳定极限不影响线性规化过程。即：

2 线性规划法的应用

线性规划法是解决多变量最优决策的方法，是在各种相互关联的多变量约束条件下，解决或规划一个对象的线性目标函数最优的问题。

定理：对于一个线性规划问题，假设它的一组可行性解有界且非空，则这组解中的极值点是最优解。

对于本文所研究的问题，定义一组可行性解为：

首先证明这组可行性解有界：

1）系统稳定情况下，ΔΡmi≥0

∵所有的αi＜0，∴Δ （ΔV）≤0，⇒0≤ΔΡmi≤

2）系统不稳定情况下，ΔΡmi≤0

∵所有的αi＜0，∴Δ（ΔV）≥0，

因此，此线性规划问题有界，并且极值点出现在约束方程与零轴交点处。换言之，最优解将出现在各发电机分别切负荷时。这样，解会显示出支路潮流极限变化情况。

并且，单条支路潮流改变量为：

对于一个给定的故障，发电机 的最大值与最小值对应了提供最大与最小支路潮流极限的发电机。同时注意，提供数值上最大的支路潮流极限的发电机对应着提供数值上最小的能量裕度的发电机。ΔIl即为系统故障后仍不能满足系统稳定运行条件时所采取的切负荷量。

3 算例分析

通过简化的爱荷华17机系统作为算例，验证算法的可行性。

1）系统故障情况1如表1所示。

表1 系统故障及清除条件

通过TEF计算αi和sli计算结果如表2所示。

表2 αi和sli计算结果列表

ΔΡmi、ΔIl计算结果如表3，其中的由暂态能量函数法（TEF）和线性规划法公式4两种方法计算得来，表格的上下分别为TEF和公式4的计算结果：

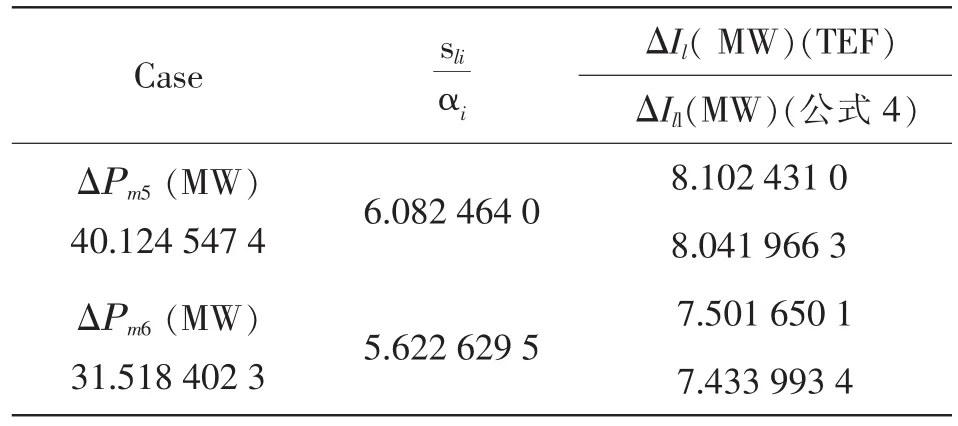
表3 ΔΡmi和ΔIl计算结果

2）系统故障情况2如表4所示。

表4 系统故障及清除条件

通过TEF计算αi和sli计算结果如表5所示：

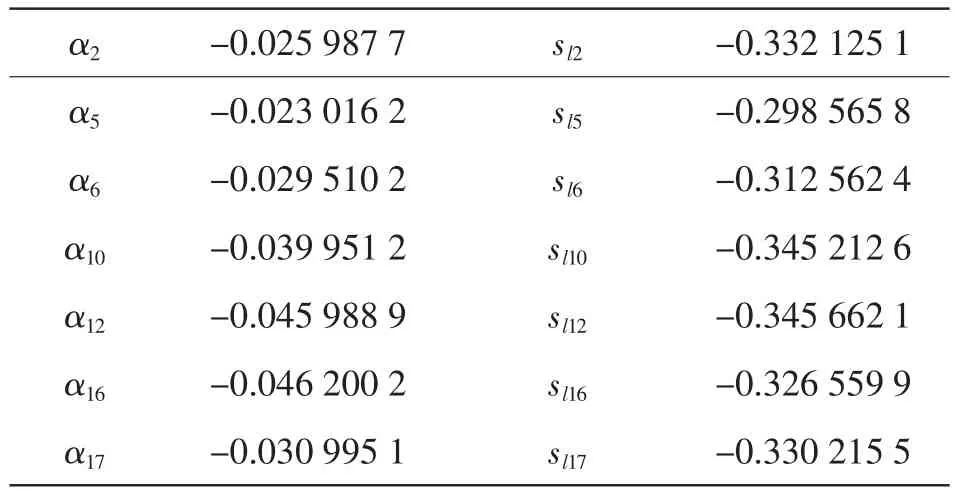
表5 αi和sli计算结果列表

ΔΡmi、ΔIl计算结果如表6，其中 的由暂态能量函数法（TEF）和线性规划法公式4两种方法计算得来，表格的上下分别为TEF和公式4的计算结果：

表6 ΔΡmi、ΔIl计算结果

4 结论

通过算例证明，用线性化了的暂态能量函数法可以快速计算出系统故障后仍不能保证安全运行时采取的紧急切负荷量。在负荷切除后，可保障系统安全运行。本文提出的基于暂态能量函数法和线性规划理论的计算暂态稳定情况下的切负荷算法，为系统的安全稳定运行提供了有效的方法。通过算例仿真计算，证明了该方法的可行性。