ZF8000/20/38型液压支架推溜参数优化

黄 勇

（潞安集团余吾煤业公司，山西 长治 046100）

采煤工作面各设备配套的合理与否，直接影响到综采机组工作效能的发挥。推移千斤顶控制回路要完成推溜和推溜工序以实现工作面的推进，但由于地质条件的差异和配套参数的不适宜，在推溜时支架底座前端会出现飘底，从而影响正常的推溜效率，因而在设计（支架、刮板输送机）和选型时都要给予重视。

1 推溜工况受力分析

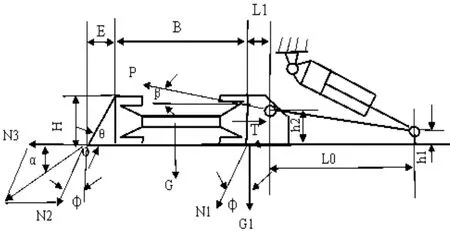
图1 推溜工况受力模型

图1中，N1、N2分别为推溜时溜槽和铲煤板对底板竖直方向的作用力，其反作用力分别为N1N、N2N，单位：N；N3为铲煤板对煤岩的水平作用力，其反作用力为N3N，单位：N；P、G分别为推溜力和溜槽的重力，单位：N；G1为相邻两侧溜槽的垂直作用力，单位：N；T为相邻两侧溜槽的水平作用力，按相邻两侧各两节溜槽的摩擦力计算T＝4Gf，单位：N，f为摩擦系数；L1、h2分别为推杆和刮板输送机铰接点的水平距离和距底板的高度，单位：m；L0、h1分别为推杆和油缸活塞杆铰接点的水平距离和距底板的高度，单位：m；B、H、E分别为溜槽的宽度、高度和铲煤板的宽度，单位：m；β、φ分别为推杆的安装角和溜槽与底板间的摩擦角，单位：°，f＝tanφ；θ为铲煤板的等效铲角，单位：°；α为N2和N3的合力与水平线的夹角，单位：°。根据受力模型可写出3个平衡方程式，分别为：

（1）对铲煤板尖端O取矩的力矩平衡方程式：

由以上三个平衡方程式可得出：

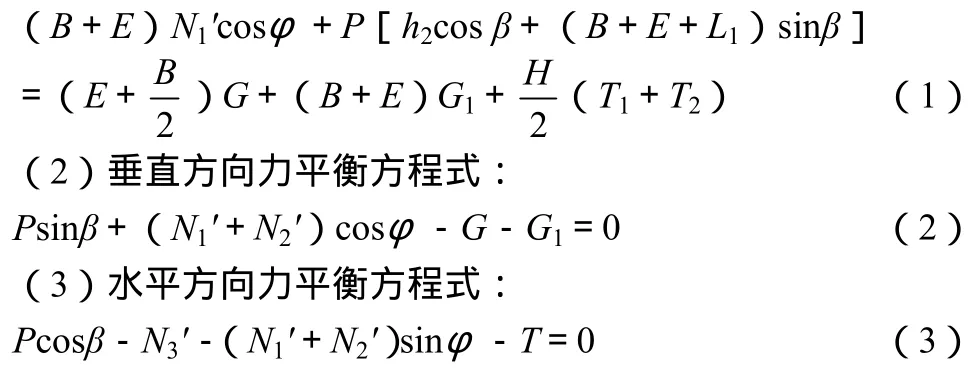
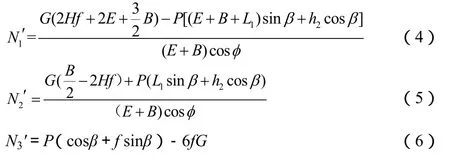
其中f＝tanφ。

由以上各式可以看出：

（1）在设计时尽量减少N1，但还要保证N1＞0，这样溜槽与推杆铰接处不会被抬起，有利于推溜。

（2）为防止推溜时飘底，当推溜力P一定时、减少推溜时的其它阻力N1，而增大N2。

（3）为使溜槽顺利移动，克服各阻力，尽量使N3增大（有效推溜力）。

（4）从受力的角度，铲煤板的铲角θ≈2α为宜，其中：

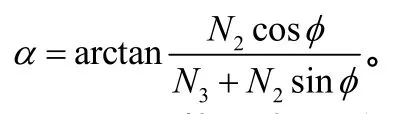
（5）从上述 3个力的表达式中可看出合理地选择一些参数，如β、h2和L1可使受力更加合理，推溜更加有效。其中β与其他参数的关系式为

2 推溜工况数学模型的建立

2.1 目标函数

从有利于推溜的角度，在液压缸推溜力P一定的条件下，增大铲煤板下铲力N2，可避免推溜时产生飘底，同时也要尽量增大N3，使溜槽顺利推移。因此，取以下两个目标函数，即N2→max、N3→max，采用线性加权法将其转化为新的单一目标函数，即F＝W1N2＋W2N3→m in，W1、W2为加权因子，根据目标函数的重要性来确定，这里W1＋W2＝－1，取W1＝－0.5，W2＝－0.5，则目标函数化为F＝－0.5N2－0.5N3→m in。

2.2 设计变量

根据设计的具体情况而定，本文则取β、h2、L1为设计变量，其他为常量，即：

X＝[X（1），X（2），X（3）]＝[β、h2、L1]

2.3 约束条件

（1）边界条件：

βmin≤β≤βmax；h2min≤h2≤h2max；L1min≤L1≤L1max

（2）保证N1大于零。如果N1小于零，则溜槽会被抬起离开底板，这将会增大推溜的附加阻力，影响正常推溜，即：

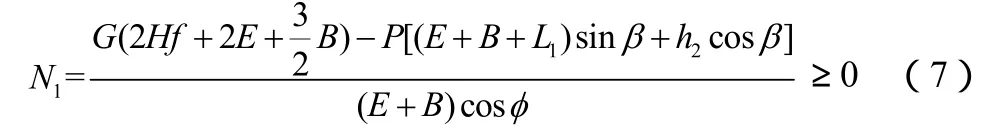
（3）相关约束。h2只能在某一区域内取值，为此则有：

h1在结构上也必须有所限制，h1min≤h1≤h1max，而，

3 基于MATLAB的推溜参数优化

3.1 ZF8000/20/38型液压支架的设计参数

G＝1.1×104N，P＝105N，B＝0.73 m，H＝0.22 m，E＝0.14 m，L0＝1.50 m，0.15 m≤L1≤0.25 m，0.08 m≤h1≤0.22 m，0.10 m≤h2≤0.20 m，－5 °≤β≤5 °，f＝0.65，φ＝33 °。

3.2 编写目标函数与约束条件的M文件

在MATLAB界面下利用文件编辑器编写目标函数的M文件如下：

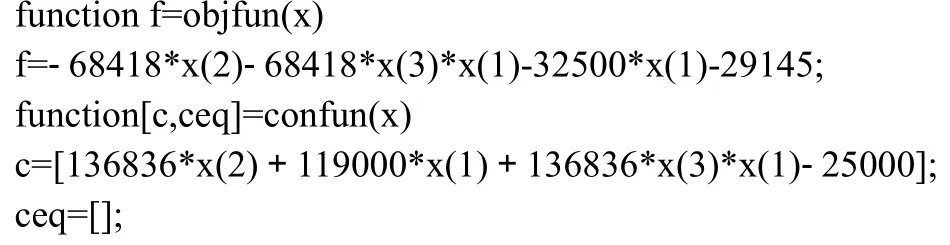
在命令窗口输入：

然后按回车键输出结果如下：

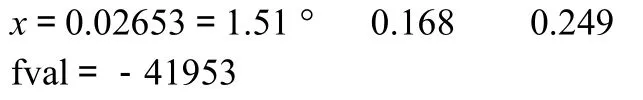
将原始方案和优化方案进行对比，结果见表1。

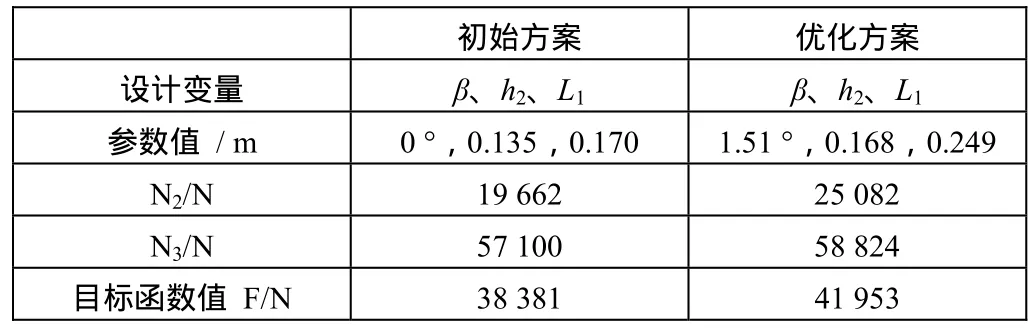
表1 初始方案与优化方案对比

由表1可以看出：优化后N2、N3都明显增大，经计算N1＝2 049 N，满足保证N1大于零的约束条件，这样就有利于避免推溜时飘底，提高推溜效率。

4 结束语

本文根据ZF8000/20/38型支架推溜工况的受力模型，建立了设计变量的目标函数与约束条件，并采用MATLAB软件对推溜联接参数进行了优化，为推溜时能够更有效地避免飘底、提高推溜效率提供了参考依据。通过分析可以看出，本文提出的方法可行，这对液压支架的设计和选型有一定的参考价值。

1 黄自强、何青则、何振华.液压支架的技术现状及发展趋势[J].山西机械，2010（4）49～50

2 全国煤炭技工教材编委会.矿山电力拖动与控制[M].北京：煤炭工业出版社，2002：147～151

3 史元伟.MATLAB开发与应用[M].北京：清华大学出版社，2008：12～15

4 黄永安等.MATLAB应用实例[M].北京：清华大学出版社，2008：35～37