机械系统中干摩擦模型的力学分析

张 聪

（太钢集团临汾钢铁有限公司，山西 临汾 041000）

机械系统的减震缓冲装置中，近年来广泛出现了一类具有非线性迟滞特性的干摩擦阻尼元件，如钢丝绳、金属橡胶减震器等。该类干摩擦减震装置的使用，大幅降低了振动系统的振幅，是一类有效的被动减震装置。

欲加装具有合适参数的干摩擦减震元件，就必须充分了解干摩擦阻尼的产生机理，建立精确但又计算量可以控制的力学模型，才能更好的指导生产实践，缩短产品的开发周期。为此，国内外的众多学者对干摩擦的力学行为开展了广泛、深入而卓有成效的研究。1931年，Den提出了著名的Coulomb摩擦模型来表示干摩擦，并求得了系统的解析解。1945年，Iwan在他的博士论文中提出了双折线模型来模拟干摩擦，也求得了两自由度振动系统的响应。近年来，出现了Bouc－Wen模型、刷子模型等较为复杂的力学模型，其虽能更精确的表达干摩擦的力学性质，但其振动响应的求解却有相当的难度。

本文针对一机械系统中的干摩擦元件，对以往研究中涉及该类干摩擦元件的建模、数值求解技术、分析方法、参数识别方法等展开综述，系统分析了干摩擦元件在减震降噪装置中的突出作用。

1 干摩擦元件的建模

关于摩擦副间的干摩擦建模，学界已提出了众多的数学模型。其中，具有开创性和代表性的是 sgn模型，即库伦摩擦模型。假设一物体在干摩擦交接面上运动，干摩擦总是阻碍物体的运动，因此，干摩擦力的大小不变，方向总与运动方向相反，其变化规律可表示如下：

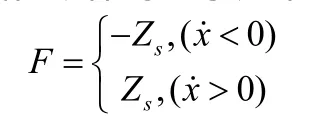
其中，F为干摩擦阻力的大小，x为物体的运动速度。然而，大量的实验研究表明，物体与干摩擦表面相接触时，物体速度方向的改变并不是突然发生的，而是存在一个过渡过程。由于接触面本身有一定的弹性，在外力的作用下，造成了接触面有一定的弹性变形。当外力的方向改变时，物体的运动方向并没有立刻改变，当外力的大小增大到一定程度，物体与接触面才产生相对位移。

考虑到接触面的弹性性质，Iwan在1961年提出了著名的双折线迟滞模型，该模型将干摩擦阻力看成一根弹簧和一个标准的coulomb摩擦副串联，且能更好的表达干摩擦阻力的非线性性质。

近年来，学术界出现了对双折线迟滞模型的修正，比如，考虑到摩擦系数不是常数的情况，摩擦副间微观滑动、二维滑动等情况，提出了如Bouc－Wen模型、刷子模型、一阶微分方程模型等描述干摩擦的数学模型，但这些模型的求解均有一定的难度。

2 干摩擦模型的数值求解技术

一个含有干摩擦交接副的力学系统，描述其集中质量运动响应的均是微分方程。但由于干摩擦阻力的存在，使得该微分方程有较强的非线性，这给求解带来了不小的难度。

对于库伦摩擦模型的求解，由于存在符号函数sgn，使得方程在速度零点不连续、不可微，可先将sgn函数在零点用Taylor公式展开，忽略高阶小量，再采取数值方法，如IHB方法（增量谐波平衡法）、HB方法（谐波平衡法）、Newmark法等求解。

对于双折线模型的求解，可先求出双折线模型弹——塑——弹的交接点，确定系统运动微分方程分别在弹、塑性区域的分段线性微分方程，再采用Runge－Kutta方法（龙格库塔方法）求解分段线性微分方程，最后将微分方程的解组装成整个时域阶段的解。这一求解方法，相对于含符号函数sgn的库伦摩擦模型求解方法，显得更为清晰明了，对解的计算精度也更好掌握，故有大量的数值算例、结果分析的报道。

3 干摩擦模型的参数识别和响应分析

对于干摩擦力学模型的参数识别，关键是识别出力学模型中的具体物理参数。目前，对众多干摩擦力学模型的参数识别研究中，集中体现在对双折线模型和Bouc－Wen模型的参数识别中。

我国学者胡海岩、李岳峰、白鸿柏、李冬伟分别采用了最小二乘辨识法、能量法、参数分离法等识别了双折线模型的刚度、滑移极限、黏性阻尼系数等参数，均取得了较为满意的效果。

国外很多学者对Bouc－Wen模型的参数识别展开了研究，采用了微分进化优化算法、遗传算法、粒子群算法、蚁群算法等人工智能方法识别了Bouc－Wen模型的参数。

4 结束语

本文系统论述、报道了干摩擦元件的建模、求解、参数识别方法，不足之处请予指正。