基于增广有色Petri网带封锁机制的并发控制模型

陈彦舟 冯朝辉

中国人民公安大学信息安全系 北京 102600

0 引言

数据库管理系统(DBMS)的一个主要功能是进行数据控制，其中并发控制又是数据控制当中的一个重要内容。并发控制要解决的问题就是串行化调度与死锁检测，进而破坏死锁，使系统得以继续运行。通常使用各种协议来对并发事务对数据库的访问进行控制。目前最常用的封锁协议是2PL协议。但是满足2PL协议的调度却有可能会带来死锁和活锁问题。

Petri网是一种能很好地描述和分析验证系统动态性能的工具。研究人员们很自然地用Petri网去描述和学习并发控制系统。如在FMS中，Petri网得到很好的应用。文献[1]通过建立并发事务共享数据资源的普通Petri网模型，探讨了可串行化调度与死锁检测问题，但是当系统涉及的事务与数据资源较多时，所构造的Petri网模型过于复杂，出现状态“爆炸”现象。

1 并发事务带封锁机制的增广有色Petri网模型

本文讨论的数据库系统有n个并发事务Ti(1 ≤i≤n)和m个共享资源Dj(1 ≤j≤m)。各事务对共享资源的加锁情况用矩阵Ln×m表示元素lij定义如下：

定义1：抑制弧/容许弧

（1）FI⊆ (P×T)为抑制弧集，F∏⊆ (P×T)为容许弧集，且FI∩F∏=φ，(FI∪F∏) ∩F=φ；

（2）W: (FI∪F∏) → {0}。

定义2：设PI(P∏)表示与抑制弧(容许弧)关联的库所之集合，t在M下可使能发生，当且仅当：

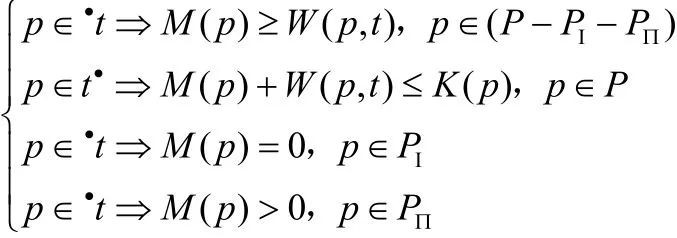
若M[t＞，则t在M下可以使能发生M[t＞M′，则M′的定义是：

2 建立ECPN_LM模型

定义 3：一个描述并发事务竞争共享资源的带封锁机制的扩展有色Petri网是一个九元组：

ECPN_LM=(P，T；F，FI，F∏，C，I-，I+，M。)

其中：P是库所的有限集合；T是变迁的有限集合；F=PT∪TP是普通有向弧的有限集合；FI是抑制弧集合；F∏是容许弧集合；C是颜色集合；I-是PT上的负函数；I+是 P T上的正函数，它们的规则与含义如下：pd是可利用共享资源；per是各事务申请对各共享资源加共享锁情况；pew是各事务申请对各共享资源加排它锁情况；pdr是事务等待读共享资源状态；ppr是事务准备读共享资源状态；ppw是事务准备写共享资源状态；pr是事务读共享资源状态；pw是事务写共享资源状态；psl是第一个事务对同一共享资源加共享锁状态；ps是共享锁；px是排它锁；pl是 事务完成读或写操作后离开状态。tdr是事务进入等待状态；tpr是事务准备读；tpw是事务准备写；tdpr是等待的事务准备读；tus是事务不申请共享锁；ts是事务申请共享锁(第一个对此共享资源加的共享锁)；tx是事务申请排它锁；tsu是事务解开共享锁；trl是事务完成读后准备离开；twl是事务完成写后准备离开。

F={(per,tpr)，(pew,tpw)，(pd,tpr)，(pd,tpw)，(tpr,pd)，(tpw,pd)，(tpr,ppr)，(tpw,ppw)，(ppr,tus)，(ppr,ts)，(ppw,tx)，(ps,ts)，(px,tx)，(tus,pr)，(ts,pr)，(ts,psl)，(psl,tsu)，(tsu,ps)，(tx,pw)，(twl,px)，(pw,twl)，(pr,trl)，(trl,pl)，(twl,pl)，(per,tdr) ，(tdr,pdr)，(pdr,tdpr)，(tdpr,ppr)}。

FI={(ppw,tpr)，(pdr,tpr)，(ppw,tdpr)，(ps,tus)，(ppr,tsu)，(ppw,tsu)，(pew,tsu)，(pdr,twl)，(per,twl)，(pew,trl)，(ppw,trl)}。

F∏={(ppw,tdr)，(px,tus)，(px,ts)，(ps,tx)}。

C={(T1)，(T2)，… ，(Tn)，(D1)，(D2)，… ，(Dm)，(R)，(W)，(S1)，(S2)，… ，(Sm)，(X1)，(X2)，… ，(Xm)，(Tl1)，(Tl2)，…，(Tln)}，颜色(Ti)(1≤i≤n)与各事务相对应；颜色(Dj)(1≤j≤m)与各共享资源相对应；颜色(R)与(W)分别对应读操作和写操作；颜色(Sj)与(Xj)(1≤j≤m)分别对应各共享资源的共享锁和排它锁；颜色(Tli)(1≤i≤n)对应各事务完成读或写离开；颜色(Ti,R,Dj)(1≤i≤n且1≤j≤m)表示事务Ti读共享资源Dj；颜色(Ti,W,Dj)(1≤i≤n且1≤j≤m)表示事务Ti写共享资源Dj。

F1=I-(per,tpr/ (Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F2=I-(pew,tpw/(Ti,W,Dj) ) = (Ti,W,Dj) , (lij= - 1 , 1 ≤i≤n,1≤j≤m)

F3=I-(pd,tpr/(Ti,R,Dj) ) = (Dj) , (lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F4=I-(pd,tpw/(Ti,W,Dj) ) = (Dj) , (lij= - 1 , 1 ≤i≤n,1≤j≤m)

F9=I-(ppr,tus/(Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F10=I-(ppr,ts/(Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F11=I-(ppw,tx/(Ti,W,Dj) ) = (Ti,W,Dj) , (lij= -1 , 1 ≤i≤n,1≤j≤m)

F12=I-(ps,ts/(Ti,R,Dj) ) = (Sj) , (lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F13=I-(px,tx/ (Ti,W,Dj) ) = (Xj) , (lij= -1 , 1 ≤i≤n,1≤j≤m)

F17=I-(psl,tsu/ (Sj) ) = (Sj) , (lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F21=I-(pw,twl/ (Ti,W,Dj) ) = (Ti,W,Dj) , (lij= - 1 , 1 ≤i≤n,1≤j≤m)

F22=I-(pr,trl/ (Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F25=I-(per,tdr/ (Ti,R,Dj))= (Ti,R,Dj),(lij= 1 , 1 ≤i≤n, 1≤j≤m)

F27=I-(pdr,tdpr/ (Ti,R,Dj)) = (Ti,R,Dj),(lij= 1 , 1 ≤i≤n,1≤j≤m)

F5=I+(pd,tpr/ (Ti,R,Dj)) = (Dj) , (lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F6=I+(pd,tpw/(Ti,W,Dj) ) = (Dj) , (lij= -1 , 1 ≤i≤n,1≤j≤m)

F7=I+(ppr,tpr/ (Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F8=I+(ppw,tpw/(Ti,W,Dj) ) = (Ti,W,Dj) , (lij= - 1 , 1 ≤i≤n,1≤j≤m)

F14=I+(pr,tus/(Ti,R,Dj))= (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F15=I+(pr,ts/ (Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F16=I+(psl,ts/ (Ti,R,Dj) ) = (Sj) ,(lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F18=I+(ps,tsu/ (Sj) ) = (Sj) , (lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F19=I+(pw,tx/ (Ti,W,Dj) ) = (Ti,W,Dj) , (lij= - 1 , 1 ≤i≤n,1≤j≤m)

F20=I+(px,twl/ (Ti,W,Dj) ) = (Xj) ,(lij= -1 , 1 ≤i≤n,1≤j≤m)

F23=I+(pl,trl/ (Ti,R,Dj) ) = (Tli) , (lij= 1 , 1 ≤i≤n, 1 ≤j≤m)

F24=I+(pl,twl/ (Ti,W,Dj) ) = (Tli) , (lij= -1 , 1 ≤i≤n,1≤j≤m)

F26=I+(pdr,tdr/ (Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

F28=I+(ppr,tdpr/ (Ti,R,Dj) ) = (Ti,R,Dj) , (lij= 1 , 1 ≤i≤n,1≤j≤m)

FI1=I-(ppw,tpr/ (Ti,R,Dj) ) = { (Tk,W,Dj) } ∩M(ppw) , (lij=1,lkj= -1,1 ≤i,k≤n, 1 ≤j≤m)

FI2=I-(pdr,tpr/ (Ti,R,Dj) ) = { (Tk,R,Dj) } ∩M(pdr) ,(lij=lkj=1,1 ≤i,k≤n, 1 ≤j≤m)

FI3=I-(ppw,tdpr/ (Ti,R,Dj) ) = { (Tk,W,Dj) } ∩M(ppw),(lij= 1 ,lkj= -1,1 ≤i,k≤n, 1 ≤j≤m)

FI4=I-(ps,tus/ (Ti,R,Dj) ) =M(ps) ,(lij= 1 , 1 ≤i≤n,1≤j≤m)

FI5=I-(ppr,tsu/ (Sj) ) = { (Tk,R,Dj) } ∩M(ppr) ,(lkj=1,1 ≤k≤n, 1 ≤j≤m)

FI6=I-(ppw,tsu/ (Sj) ) = ( { (Ti,W,Dk) } ∩M(ppw))∧

({(Ti,R,Dj) } ∩M(pr) ),(lij= 1 ,lik= -1,1 ≤i≤n, 1 ≤j,k≤m)

FI7=I-(pew,tsu/ (Sj) ) = ( { (Ti,W,Dk) } ∩M(pew))∧

({(Ti,R,Dj) } ∩M(pr) ),(lij= 1 ,lik=-1,1 ≤i≤n, 1 ≤j,k≤m)

FI8=I-(pdr,twl/ (Ti,W,Dj) ) = { (Ti,R,Dk) } ∩M(pdr) ,(lij=- 1 ,lik= 1,1 ≤i≤n, 1 ≤j,k≤m)

FI9=I-(per,twl/ (Ti,W,Dj) ) = { (Ti,R,Dk) } ∩M(per) ,(lij=- 1 ,lik= 1,1 ≤i≤n, 1 ≤j,k≤m)

FI10=I-(pew,trl/ (Ti,R,Dj) ) = { (Ti,W,Dk) } ∩M(pew),(lij= 1 ,lik= -1,1 ≤i≤n, 1 ≤j,k≤m)

FI11=I-(ppw,trl/ (Ti,R,Dj) ) = { (Ti,W,Dk) } ∩M(ppw),(lij= 1 ,lik= -1,1 ≤i≤n, 1 ≤j,k≤m)

F∏1=I-(ppw,tdr/ (Ti,R,Dj) ) = { (Tk,W,Dj) } ∩M(ppw),(lij= 1 ,lik= -1,1 ≤i,k≤n, 1 ≤j≤m)

F∏2=I-(px,tus/ (Ti,R,Dj) ) = { (Xj) } ∩M(px) ,(lij=1,1≤i≤n, 1 ≤j≤m)

F∏3=I-(px,ts/ (Ti,R,Dj) ) = { (Xj) } ∩M(px) ,(lij=1,1≤i≤n, 1 ≤j≤m)

F∏4=I-(ps,tx/ (Ti,R,Dj) ) = { (Sj) } ∩M(ps) ,(lij=-1,

1 ≤i≤n, 1 ≤j≤m)

3 模型分析与验证

3.1 封锁机制的正确性分析

由 E CPN_LM模型可知，对于一个共享资源Dj(1≤j≤m)可有三个状态：无任何操作，被加了共享锁，被加了排它锁。当事务在读预备状态ppr时，如果事务操作满足ts(此时对于共享资源Dj来说，它没有被加排它锁((Xj)∈M(px))，且没有被加共享锁((Sj)∈M(ps)))，那么事务申请共享锁(ts使能发生)，同时做M(ps) - (Sj)：代表已对Dj加共享锁。当此事务在读共享资源Dj时，另一事务也进入读预备状态ppr。此时，ts不满足使能条件，而tus使能发生(因为对已加共享锁的资源Dj来说，其它进程可对它进行读操作，而不必再申请锁)。当库所ppr，ppw，pew为空时，代表最后一个读资源Dj的事务离开了且同时符合 2 PL协议(接下来会谈到)。此时，tsu使能发生，释放共享锁。根据写操作原则，对共享资源Dj的写操作每时每刻都只能有一个，所以当事务Ti在写预备状态ppw时，若对想写的共享资源Dj(Dj已加共享锁((Sj)∉M(ps))，又或者先前已有事务对Dj加了排它锁((Xj)∉M(px)))，那么tx不能发生。否则tx将使能发生并对资源Dj加排它锁。当Ti进入写操作状态pw后，只有符合2PL协议后，twl才使能发生，解开排它锁。

3.2 写者优先分析

在ECPN_LM模型中，当某时刻有事务Ti(1≤i≤n)要对Dj(1≤j≤m)进行写操作，此时来到写预备状态，并通过抑制弧抑制后来的想对共享资源Dj进行读操作的事务。若系统内已存在对资源Dj进行读操作的事务((Sj)∉M(ps))，那么tx不能发生，只有这些读Dj的事务全部读完并离开((Sj)∈M(ps))时，tx才能发生。然后事务Ti对资源Dj加排它锁，并且进入写操作pw，而此时其它想对共享资源Dj进行读操作的事务可进入读预备状态ppr并等待共享锁。

3.3 满足2PL协议分析

在ECPN_LM模型中，由FI6，FI7，FI8，FI9四条抑制弧来保证调度满足 2PL。变迁tsu要想在(Sj) (即最后一个事务解除对共享资源Dj所加的共享锁)情况下发生，那么库所pew，ppw中的标识和库所ppr中的标识必须被全部移走，即事务Ti只有在获得所需的全部锁之后才能解除其对共享资源Dj所加的共享锁。而当tl发生后，事务Ti不再有读写操作。同理，变迁twl要想在(Xj) (即事务解除对共享资源Dj所加的排它锁)情况下发生，那么库所per，pdr中的标识必须被全部移走，即事务Ti只有在获得所需的全部锁之后才能解除其对共享资源Dj所加的排它锁。因此其变迁发生的序列所对应的调度满足2PL。

3.4 系统无活锁分析

在 ECPN_LM 模型中，若有事务欲对共享资源Dj(1≤j≤m)进行写操作，且此事务已进入写预备状态ppw，那么往后所有欲对共享资源Dj进行读操作的事务将进入等待状态pdr(由抑制弧FI1和容许弧F∏1实现)。当写Dj的事务进入写操作(tx使能发生)时，所有因等待读Dj的等待事务进入读预备状态ppr，且通过抑制弧FI2实现先来先服务。注：库所pdr的标识的颜色集按队列排队。

3.5 死锁检测分析

设调度s由 R MG(ECPN_LM)中从M。到端点M的路径上的变迁列组成的，则s是死锁状态，当且仅当M(pr) ≠ 0或M(pw) ≠ 0 。注：可达标识图 RMG(ECPN_LM)可由文献[2]中所提到的算法构造。

假设s是死锁状态，说明s中必存在两个以上的事务，它们由于相互拥有对方所需资源的锁而无法运行。

假设数据库系统有两个并发事务(T1,T2)，竞争两个共享资源(D1,D2)，其中T1要求对资源D1加共享锁，对资源D2加排它锁；T2要求对资源D1加排它锁，对资源D2加共享锁，加锁矩阵为那么按ECPN_LM模型运行至以下任一种情况：

系统出现死锁状态，所以若调度从M。到端点M′或者M′的路径上的变迁列组成，则系统会出现死锁状态。

若按ECPN_LM模型运行至以下情况：

(Tl1) + (Tl2))，系统不出现死锁状态，所以若调度由从M。到端点M′的路径上的变迁序列组成，则系统不会出现死锁状态，且该调度为可串行化调度。

4 结论

本模型在一定程度上有适用性，但还有很多问题没有解决，如：用户优先级问题，中断处理问题，安全性检测问题，数据恢复问题。所以很多问题还需进一步探讨。

[1]HAN Yao-jun.WU Zhe-hui.Petri net-based serializability and deadlock detection in concurrency control of database[A].第十七届全国数据库学术会议论文集[c].保定:河北大学出版社.2000.

[2]韩耀军,蒋昌俊,罗雪梅.数据库系统并发控制的扩展有色Petri网方法[J].同济大学学报(自然科学版).2004.

[3]韩耀军,罗雪梅,蒋昌俊.扩展 Petri网在实时数据库并发控制中的应用[J].系统仿真学报.2003.

[4]左凤朝.基于Petri网的数据库系统并发控制模型[J].计算机工程与应用.2002.