面向齿轮箱故障诊断的序贯概率比检验理论和方法
尚云飞,陈汉新,孙 魁
(武汉工程大学机电工程学院,湖北 武汉,430205)
0 引 言
1947年,Wald[1]提出了序贯概率比检验算法.该算法基于两种假设:(1)样本要满足独立同分布;(2)样本的先验分布要已知,如满足正态分布等[2].序贯概率比检验算法应用于齿轮箱的故障诊断与传统的故障诊断方法不同的是,不需要预先设定检验样本的数量,而是将序贯概率比检验后的值与预先设定的阈值进行比较,从而判断设备的运行状态[3].
在齿轮故障诊断实验中,选用齿轮裂纹来模拟齿轮故障.实验中得到的信号会夹杂着噪声等干扰,影响了信号的稳定性.首先,采用小波包降噪的方法对信号进行预处理,以得到稳定的振动信号.再运用时域分析法提取信号的特征值,最后对信号进行序贯概率比检验.为了验证序贯概率比检验算法用于齿轮箱故障诊断的诊断能力,选用均方根误差的方法来验证该方法的有效性.
1 序贯概率比检验原理

对于一个二元序贯概率比检验,零假设和被择假设分别表示为H0∶θ=θ0和H1∶θ=θ1.它们的联合分布密度函数为
(1)
其中,j=0,1.序贯概率比检验的似然比λ为
λn(x)=λn(x1,…,xn)=
(2)
假设x1是采样得到的第一个观测数据值,将其带入公式(2)中计算似然比,记为λ1(x1).按预先设定的阈值对两种故障模式进行识别.如果似然比满足λ1(x1)
民营企业从银行获得贷款也不容易。“银行能给我们的贷款额度在收紧。”某文旅企业负责人周珊彤说,“我们找银行贷款,额度上就会打折扣,放款也不能一次到位,而是要分几批发放,银行的解释是上级行对规模管理得较严。”
根据假设检验中犯第一类错误的概率α与犯第二类错误的概率β确定阈值A和B(A>B).检验中的阈值A,B与α,β的关系满足如下式子:
(3)
(4)
2 齿轮箱故障诊断实验
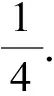

表1 两种故障模式
如图1所示的齿轮箱工作结构图,振动是由齿轮3与齿轮4之间的冲击力产生的,实验中选取齿轮3来模拟故障模式.

图1 齿轮箱工作结构图
将两个加速度传感器分别安装在齿轮箱的水平和垂直方向,采用动态模拟器来采集齿轮箱振动信号.本文只对安装在水平方向上的传感器所测得的振动信号进行分析.将正常状况下得到的振动信号记为S1,故障状况下得到的振动信号记为S2.
3 齿轮裂纹的序贯概率比检验
3.1 小波包降噪
小波包变换通过对信号的低频部分和高频部分的同时分解来提高时频分辨率.将实验信号进行3层小波包分解,就可以得到8个正交频带的振动信号,再对信号进行重构[4].这可以对信号处理得更细致、准确.得到适合序贯概率比检验的平稳信号.
3.2 特征参数提取
特征参数可以反映振动信号的特征信息,从原始振动信号中提取相关的特征参数,将其预处理后作为序贯概率比检验的检验参数[5-8].实验中的离散待检信号xi=[x1,x2,…,xN],N=8 192,每组取1 024个检验点,这样就可以得到7 169组检验数据.几个特征参数按下面公式计算:
均值:
(5)
峭度值:
(6)
峭度值的所有取值作为作为序贯概率比检验的检验参数,表示为ki=[k1,…,kn],其均值和标准差为:
均值:
(7)
标准差:
(8)
3.3 齿轮裂纹的序贯概率比检验
由序贯概率比检验的基本原理可知,待检验序列的均值和方差对似然比有较大的影响.经过预处理后,几组检验参数的序列基本满足高斯分布.在正常状况下,该信号序列满足零假设H0∶μ=μ0;在故障状况下,该信号序列满足被择假设H1∶μ=μ1.标准差σ不变,均值变化,在零假设和备择假设均成立的条件下,该序列的联合概率密度分别表示为:
(9)
(10)
式(10)中,p0i和p1i分别为零假设和备择假设条件下的概率密度函数.序贯概率比检验的似然比为
(11)
式(11)中,P0和P1分别为零假设和备择假设条件下的先验概率.
在实际应用中,为了计算方便且准确,公式(11)可以转化为下面形式[9]:
(12)
此时,阈值a=lnA,b=lnB.
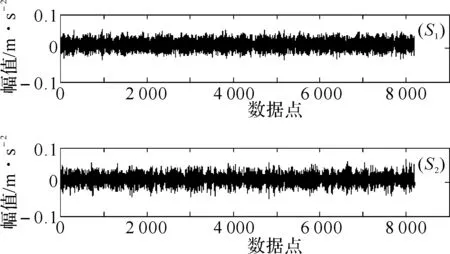
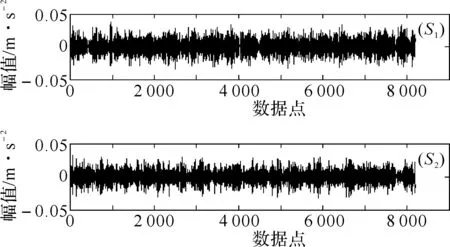
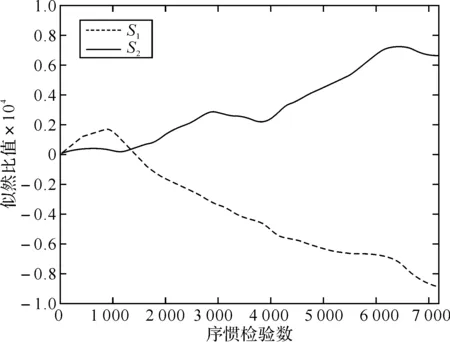
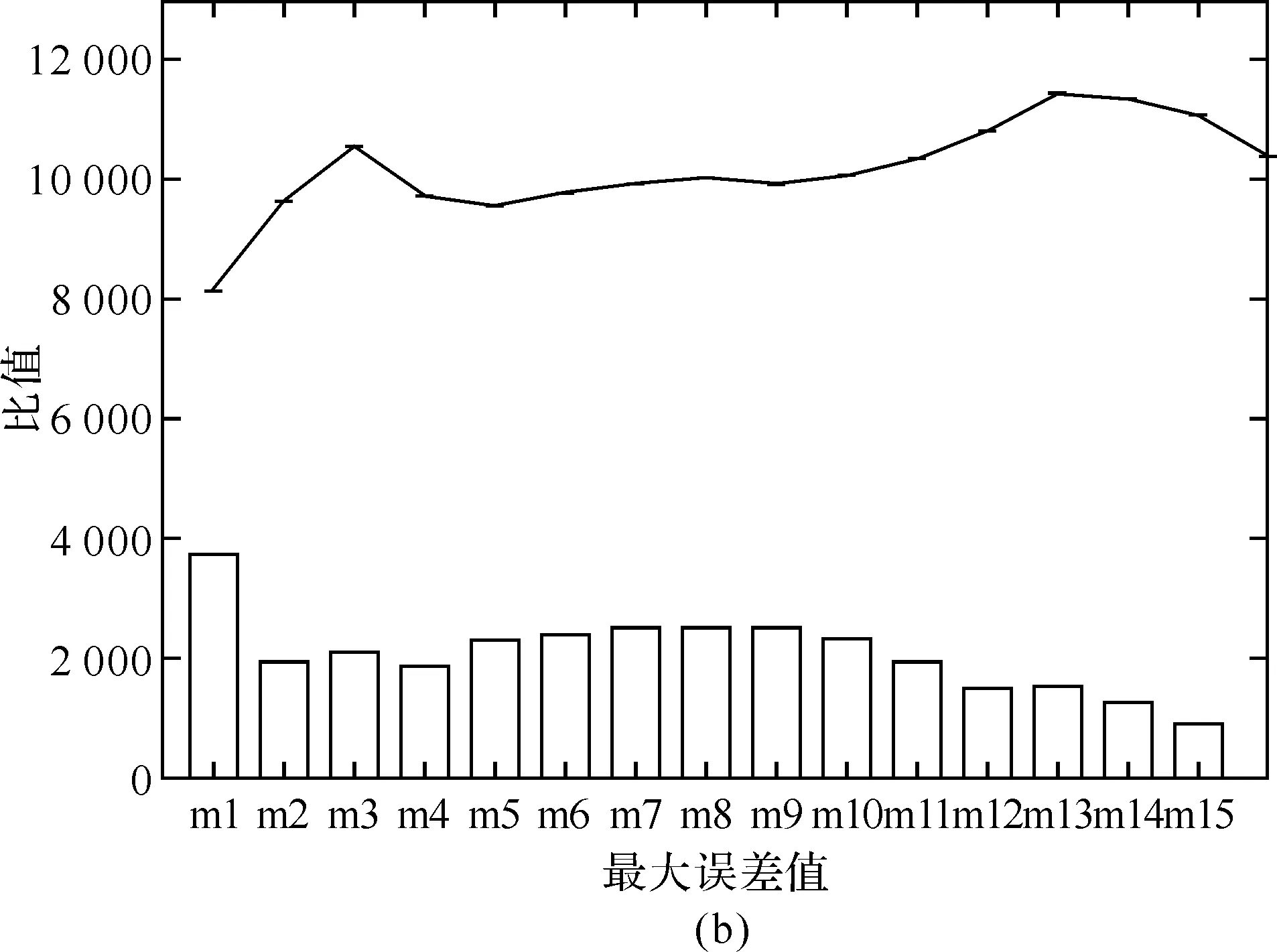
如果似然比满足Δ 图2 齿轮箱序贯概率比检验流程图 为了检验采用序贯概率比检验算法对齿轮裂纹进行故障诊断的诊断性能和可行性,用均方根误差算法来评估其诊断能力.均方根误差定义为: (13) 对于正常状况和故障状况两种故障模式,实验中共得到图3所示的S1和S2两组振动信号. 图3 两组实验振动信号:(S1)为正常状况;(S2)为故障状况 对实验信号进行小波包去噪处理,得到稳定的信号,如图4所示. 图4 小波包去噪后的振动信号,(S1)为正常状况;(S2)为故障状况 峭度值对冲击性特性很敏感,均值偏差对似然比、检验时间的长短以及检验的准确性都有影响.对假设H0和H1,规定犯第一类错误的概率与犯第二类错误的概率相等,取α=β=0.005,并且所观测信号的先验概率是相等的. 由序贯概率比检验的基本原理可知,均值变化量对似然比Δ的影响较大.以正常状况下的信号S1的均值作为参数μ0,以故障状态下的信号S2的均值作为参数μ1,对信号进行检验,得到如图5所示的图形. 图5 以正常状况下的信号S1的均值作为参数μ0,以故障状态下的信号S2的均值作为参数μ1的序贯概率比检验结果 当以正常状况下的信号S1的均值作为参数μ0,以故障状态下的信号S2的均值作为参数μ1时,分别将信号S1和S2输入似然比公式中检验,得到图5.图5说明输入信号S1时,似然比满足Δ 实验中,在正常状况下获得两组实验数据,每一组预处理并提取特征值后得到7 169个数据点,两组信号就共有14 338个数据点.将这些数据点分为16小组,分别记为A1,B1,C1,D1,E1,F1,G1,H1,I1,J1,K1,L1,M1,N1,O1,P1组.将每一组数据进行序贯概率比检验,得到16个似然比的值,分别记为A2,B2,C2,D2,E2,F2,G2,H2,I2,J2,K2,L2,M2,N2,O2,P2.用均方根误差方法来计算这16个似然比之间的误差,即A2分别与B2到P2这15个似然比比较,B2分别与C2到P2这14个似然比比较,C2分别与D2到P2这13个似然比比较,…,O2与P2比较,得到15组比值,其中每组比值中的最大值分别如以下图中所示的m1,m2,m3,…,m15.故障模式下计算的似然比记为a,运用均方根误差算法分别与上面的16组似然比值比较,即a与A2,B2…P2比较,计算不同故障模式之间的误差,共得到到16个误差值点,形成的误差曲线如下面图中的曲线.通过误差的比较来评估序贯概率比检验算法应用于齿轮裂纹的故障诊断的诊断能力. 以正常信号的均值作为参数μ0,以故障信号的均值作为参数μ1,建立序贯概率比检验模型.检验结果如图6所示. 将实验中得到并预处理后的14 338个正常齿轮的数据信号,分为16组,进行序贯概率比检验,得到图6(a)所示的16条normal曲线.同理,对故障的数据信号进行序贯概率比检验,得到图6(a)所示的fault曲线.图6(a)说明16组正常信号的似然比曲线大体趋势相同,与故障信号的似然比曲线有明显的差异.运用均方根误差算法计算16组正常信号的似然比之间的误差,共得到15组误差数据,每组误差数据中的最大值如图6(b)中的条形图所示.继续计算故障信号分别与正常信号似然比之间的误差,得到如图6(b)所示的误差曲线.图6(b)说明不同故障模式之间的误差远大于同种故障模式彼此之间的误差,也就是说,序贯概率比检验算法可以对不同故障模式进行有效的分类和识别. 图6 16组正常信号和故障信号的序贯概率比检验及误差计算 基于序贯概率比检验算法建立了一种新的齿轮箱故障诊断模型.通过对正常和故障齿轮状态的识别与检验,来检验序贯概率比检验算法的有效性.实验中得到的振动信号夹杂着噪声等干扰,采用小波包去噪方法对原信号进行预处理,得到稳定的检验信号.采用时域分析法提取信号的特征值,本文中提取对冲击性振动敏感的峭度值作为特征值.运用均方根误差算法来检验序贯概率比检验算法的诊断能力.结果表明本文提出的方法能够有效地对齿轮进行故障诊断.序贯概率比检验算法对齿轮裂纹的识别和诊断具有很好的有效性和可行性.此外,上述方法也适用于复杂旋转机械的故障诊断与检测. 参考文献: [1]Wald A.Sequential Analysis[M].New York:Wiley,1947. [2]Yu Chenggang,Su Bingjing.A non-parametric sequential rank-sum probability ratio test method for binary hypothesis testing[J].Signal Processing,2004(84):1267-1272. [3]李炜,朱芸,毛海杰,等.SPRT检验法和小波变换法在管道泄漏检测中的应用[J].计算机测量与控制,2005(9):903-904. [4]舒苗淼,刘广璞,潘宏侠.基于小波包分解的机械振动信号分析[J].起重运输机械,2009(9):61-64. [5]鲁艳军,陈汉新,贺文杰,等.基于混合特征提取和WNN的齿轮箱故障诊断[J].武汉工程大学学报,2011,33(5):82-88. [6]陈汉新,王庆军,陈绪兵,等.基于解调振动信号特征提取齿轮箱的故障诊断[J].武汉工程大学学报,2010,32(9):67-77. [7]贺文杰,Bajolet Julien,Yoann Plassard,等.基于EMD和FFT的齿轮箱故障诊断[J].武汉工程大学学报,2011,33(1):65-70. [8]安妮,徐建民.齿轮箱振动的故障诊断与实例分析[J].武汉工程大学学报,2011,33(12):70-72. [9]Min Z H,Sun L M.A novel non-parametric sequential probability ratio test method for structural condition assessment[C]∥Health Monitoring of Structural and Biological Systems.Edited by Kundu,Tribikram,Proceedings of the SPIE,2010(7650):1-9.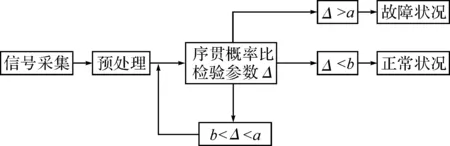
3.4 误差分析
4 结果与分析
4.1 实验结果
4.2 预处理结果
4.3 序贯概率比检验结果分析
4.4 误差结果分析

5 结 语

