车体结构振动模态仿真与试验一致性分析

赵红伟，田爱琴，王万静，丁叁叁

(中国南车集团 青岛四方机车车辆股份有限公司 技术中心，山东 青岛 266111)

0 引言

行驶中的车辆受到多种激振，研究车体动态特性能有效地分析整车的振动舒适性、行驶平顺性、安全性及寿命，其目的在于优化车身结构以控制车体模态频率与模态振型.车体模态分析不仅可用来分析整车的性能，还可直接对其结构设计进行评价.近年来国内许多学者在车体的模态分析中进行了不懈的努力和探索，机车和动车组钢结构车体的自由模态分析［1-2］，针对不同类型车体钢结构自由模态做了深入的研究并取得了很好的结果;客车车体整备状态的自由模态分析［3］，对客车车辆质量的分布做了有意义的分析，却没有试验数据的支撑.本文通过对比分析仿真和试验数据，结合工程中的应用及车体结构研发经验，采用参数优化的方式解决车体模态分析中仿真与试验数据的差异性问题，并对车辆不同运用状态中的支撑刚度系数得出一个定性的认识.

1 模态分析理论基础

模态分析的实质就是求解具有有限个自由度的无阻尼线弹性系统运动方程.由于车体结构极为复杂，不可能用解析法求得其振动模态，而只好借助于有限元方法，其求解的基本原理如下.

有限元模型的自由振动方程可写为

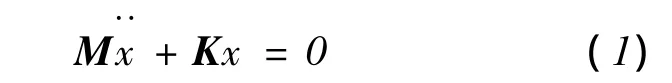
式中，M为车体有限元模型的总体质量矩阵，为一正定矩阵;K为车体有限元模型的总体刚度矩阵，为一半正定矩阵;x表示车体振动的位移向量.于是，车体结构自由振动的各阶固有频率ωi(i=1，2，…，n，其中n为车体有限元模型的自由度数)由以下特征方程求得

式中，ω为车体自由振动的固有频率.

当ωi为特征方程式(2)的重根时，把它代入方程

解得其对应的各个振型.

当ωi是特征方程式(2)的单根时，代入特征矩阵中

求得该特征矩阵的伴随矩阵

则该伴随矩阵的任一非零列向量即为固有频率ωi所对应的振型.

2 车体结构的模态分析

根据铝合金车体由大型中空挤压型材焊接而成的特点，建模时需按偏安全原则，尽可能细致离散车体.由于模态分析时加载均被忽略，因此车体各附加部件的质量和配重采用质量单元的方式进行施加，质量较大的车下吊挂按实际位置相加.为了更好地掌握车体的动态特性，对车体钢结构及在整备状态下的车体分别计算其固有频率及振型.

2.1 车体约束方式

在计算车体钢结构及整备状态自由模态的频率与振型时，车体处于悬浮状态，即无约束状态，这样计算出来的频率与振型完全是由车体弹性体本身决定的，不会受边界条件的影响.另一种情况是计算车体钢结构和整备约束状态模态的频率与振型时，在车体实际运用支撑点处加弹性约束，以模拟实际试验状态.

2.2 车辆整备重量的处理方法

高速车体固有频率模态分析，一个是对钢结构自振频率的计算，另一个是对整备状态下自振频率的计算.钢结构车体重量分布单一，基本没有多余的附加重量，处理起来较容易，不再赘述.对于整备状态下计算模型中的质量分布，由于车体整备时是一个包括多材料，多种连接方式复杂系统，而针对这种复杂系统的计算分析，极难准确模拟.一般来说采用两种方法:一是把车体整备状态下的自重减去车体钢结构的重量，两者之差均布到地板上.二是基本按车体整备状态时的质量分布来施加.具体描述如下:将车体布线、内装结构的重量分布于侧墙、底架，车顶以及端墙中，并相应地把重量以单元质量的形式施加到各大部件中，底架吊挂中大于300 kg的部件，则引入集中质量，作用在实际结构部件的重心处，在其重心位移以刚性杆的形式连接在底架横梁，部分不能明确分出所属区域的重量，均布在车体地板上.除以上两种方法，还有一种方法为改变密度法，通过改变组成结构材料的密度以使车体的重量等于整备车体重量，此方法在计算车体钢结构模态分析时是个常用的方法，但在整备车体模态分析时，由于其过大地增加了车体刚度，明显不适合应用在整备车体分析中.

2.3 模态分析计算结果

把车体的有限元模型导入Abaqus软件中，计算车体的自由模态分析.其模态数据如表1、2所示.表1中的试验数据是钢结构车体的地面试验数据，表2中的试验数据是整备状态时的线路试验数据.

表1 车体钢结构模态数据 Hz

表2 整备状态车体模态数据 Hz

由上表中的数据分析可知:①对比车体钢结构的计算与试验数据，菱形和一阶垂向弯曲来说是很接近的，但扭转振型差别大.②表2中的数据分析表明针对整备状态车体的两种处理方式，如从车体振型出现前后顺序考虑的话，方法1和试验接近，如只是考核对车体影响较大的一阶垂向弯曲模态频率，那么方法2中的结果和试验相对更接近些.常规分析看来，方法2中的质量分布更接近于实际车体状态，其模态不论是振型出现的先后顺序还是数值大小都应该与试验更吻合，但计算中却得出了不同的结果，其原因存在多个方面，其中之一就是计算时未考虑内装的刚度贡献，这点影响了方法2的结果准确性.而此次研究的前提要保证仿真车体振型出现的顺序和试验结果一致，至于数据大小的差异可以通过调整约束弹性刚度系数来实现，所以选择方法1作为本次研究的对象.造成试验模态和计算模态的相关度不是很高的原因有:①试验条件和计算的约束条件不同，试验模态中采用的是一种弹性支撑方式，而计算则采用自由模态分析即无约束状态;②试验是有阻尼的，在有限元模型分析中没有考虑阻尼的影响.根据自由振动就可分析出车辆系统各刚体的固有振动模态，对于线性系统来说，固有振动模态频率公式为

当C=0时，则为无阻尼的固有振动频率

对比可知f0＜f1.式中，M为振动系统的质量;K为振动系统的刚度;C为振动系统的阻尼.固有振动频率由系统的质量，刚度和阻尼决定.

3 车体弹性约束优化设计

对于结构阻尼，质量分布等不确定影响因素，在仿真计算中可以通过调整弹簧的约束刚度系数来消除.在分析有限元模型时，其弹性约束用等效线性弹簧替代.所以，需通过优化的方式调整车体约束刚度，使计算与试验数据一致.这里采用尺寸优化方法来确定弹簧三个方向上的刚度系数，通常采用的有限元尺寸优化方法，对应的数学模型为:

其中，目标函数M(x)和约束函数g是由结构分析得到的响应.由于我们重点关注的是车体的三阶振动模态(菱形、一阶垂向弯曲和扭转振型)，它们是车体设计中所占重要性较大的三阶模态，所以选择其中之一作为本次优化的目标函数，另外两个作为约束函数，约束函数的上下限值参考试验数据而定，设计变量x为弹簧支撑约束一个方向的刚度系数.

图1 弹性约束弹簧刚度参数优化迭代曲线

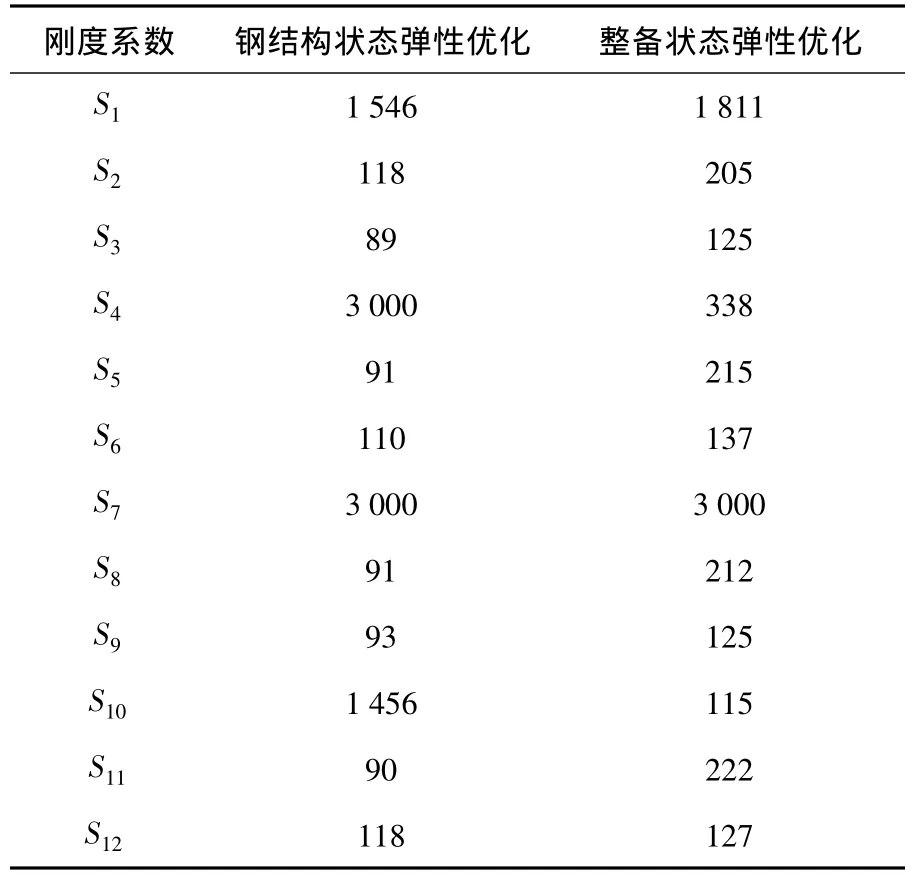
表3 约束支撑刚度系数参数优化结果 N/mm

图1所示是约束支撑弹性参数的迭代优化曲线，经过优化分析后，车体的三阶振动模态都比较好的接近真实值，达到了优化的目的.表3中的数据分别是车体钢结构和整备状态车体弹性约束优化后的刚度系数，s1，s2，…，s12代表空簧弹性支撑中弹性刚度系数，其中一个空簧处对应三个方向的约束度.表4中的数据是约束弹性刚度优化后的两种车体状态中的三阶车体模态数据.

表4 优化后车体模态仿真计算数据 Hz

综合表1，2和表4可得出车体试验与自由模态及约束模态的数据对应分析图.图2是钢结构车体模态的对比分析图，图3是整备状态车体模态的对比分析图.

图2 钢结构车体模态的对比分析图

图3 整备状态车体模态的对比分析图

通过上述弹簧刚度系数的参数优化，提高了车体在约束条件下得出的车体三阶模态与试验数据相关度，当然这个约束条件与实际会有所差异，其差异在于计算中的约束条件不仅包括线路试验中的约束刚度，还包括车体的阻尼和质量分布不确定等因素在内.参数优化后的约束条件使得车体仿真与试验模态数据相关性更高，从而改变了自由模态中某些振型试验和仿真差异较大的现象.

4 结论

试验和仿真相辅相成，互为补充.模态试验存在试验耗费大，试验周期长等多方面因素的限制.仿真计算则由于计算模型，边界条件以及认识程度高低等因素制约着其数据的准确性.本文中模态计算结果与试验结果对比只是手段，其最终目的是车体模态分析中，通过改进车体的质量分布，边界条件，使计算更能与试验互相验证.在工程允许的精度误差范围内，在以后的动车组车体模态分析中，模态计算分析作为首要选择，未尝不是没有可能.

［1］王丹，李强.高速客车车体钢结构弹性模态分析研究［J］.北方交通大学学报，2001(4):94-96.

［2］曾仲谋，肖守讷，阳光武.SS9改进型机车车体钢结构弹性模态分析研究［J］.机车电传动，2004(2):23-25.

［3］郝鲁波，胡青泥，李刚.整备状态下客车模态的有限元分析探讨［J］.铁道车辆，2004，42(11):4-7.

［4］张曙光.高速列车设计方法研究［M］.北京:中国铁道出版社，2009.

［5］冯国胜.客车车身结构的有限元分析［J］.机械工程学报，1999，35(1):91-95.

［6］王挺.机车车体第一阶模态的研究［J］.机车电传动，2003(6):24-26.

［7］沈宏峻，周劲松.铰接式客车车体的轻量化设计和模态分析［J］.铁道学报，1997，16(增刊):46-51.

［8］张胜兰，郑冬黎，郝琪，等.基于HyperWorks的结构优化设计技术［M］.北京:机械工业出版社，2007.

［9］曹树谦，张文德，萧龙翔.振动结构模态分析:理论、实验与应用.［M］.天津:天津大学出版社，2001.