XT型减振器座的拓扑优化实践

孙厚礼，马龙，周平宇

(中国南车集团 青岛四方机车车辆股份有限公司 技术中心，山东 青岛 266000)＊

0 前言

传统的机械设计大都以经验和经典理论的简单计算为基础，设计的产品结构未必能达到最优，大多都存在着一定的问题，或强度不足，或自重太重，不但造成材料浪费，成本增加，而且更能造成能源消耗的加剧.计算机技术、有限元法及数学规划理论的不断发展，让人们有了强大的结构分析工具，并且有了一套系统的方法来改进设计和优化设计，这就使靠经验值和经典理论的简单计算的传统设计方法逐步被以有限元法为基础的有限元分析和优化分析的现代设计方法所替代.产品结构设计的目的是使结构方案能够有效满足功能需要，因此结构设计问题可以说是一个优化问题，即在满足一定约束条件的前提下，通过改变某些设计变量，使产品的性能达到期望的目标.优化设计以数学规划为理论基础，将设计问题的物理模型转化为数学模型，运用最优化数学理论，以计算机和应用软件为工具，在充分考虑多种设计约束的前提下，寻求满足预定目标的最佳设计.当前，最优化技术与有限元法结合产生的结构优化技术已经逐渐发展成熟，并成功应用于产品设计的各个阶段.

拓扑优化技术能在给定的设计域空间中生成经过优化后的结构形状及材料分布.通过将设计域离散成有限单元网格，并为每个单元计算材料特性，在给定的约束条件下，利用优化算法更改材料的分布，以优化获得设计人员期望的设计目标.连续体结构拓扑优化的基本思想是将寻求结构的最优拓扑问题转化为在给定的设计区域内寻求最优材料分布的问题，通过拓扑优化分析，设计人员可以全面了解产品的结构受力分布情况和功能特征，进而有针对性地对总体结构和相关结构进行具体改进设计;连续体结构拓扑优化的最大特点是能在不知道结构拓扑形状的前提下，根据已知边界条件和载荷条件确定较合理的结构形式，为设计人员提供全新的设计和最优的材料分布方案.

本文利用大型商业软件Hyperworks的Hypermesh和Optistruct模块为工具，对机车车辆用的XT型减振器座进行了拓扑优化设计.

1 优化设计的数学模型

优化设计有三个要素:设计变量、目标函数和约束条件.设计变量是在优化过程中发生改变从而提高性能的一组参数.目标函数是要求的最优设计性能，是关于设计变量的函数.约束条件是对设计的限制，是对设计变量和其他性能的要求.其数学模型可以表述为:

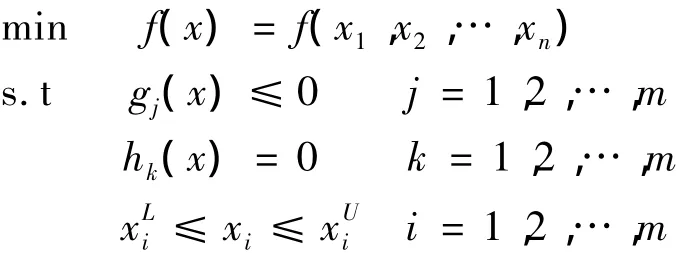
式中，f(x)是目标函数;g(x)是不等式约束函数;h(x)是等式约束函数;X=x1，x2，…，xn是设计变量;上角标L是指下限，上角标U是指上限.

在拓扑优化中，工程中常用的方法是变密度法.其基本思想是在优化过程中引入一种密度值可以在［0，1］区间连续变化的材料模型，将结构离散为一定数量的单元后，每个单元具有一个密度值，以该密度值为设计变量，建立优化模型.利用优化算法进行求解计算，然后根据计算得到的单元密度值结果决定单元或材料的取舍.密度值为1表明该单元应当保留，密度值为0表明该单元应当删除，具有中间密度材料的单元引入惩罚因子，使设计变量寻优方向向两端发展，最终通过计算决定单元的保留或删除.在删除部分单元后得到具有一定外形和内部孔洞的结构拓扑图形，即为结构应该具有的最优拓扑形式，它可以作为结构新方案的参考.

2 减振器座拓扑优化实例

本文研究对象为对机车车辆用的XT型减振器座，它是机车车辆转向架的关键部件.减振器座初始结构设计方案的有限元模型如图1所示.

图1 减振器座初始设计方案有限元模型

减振器座初始结构设计方案的左侧有8个定位螺栓孔，右侧有减振器安装凸台，质量为37.3 kg.有限元分析结果表明，初始设计方案的结构易造成工作过程中减振器座悬臂根部区域应力过大.此区域Von.Mises应力最大值为145.1 MPa(如图2所示)，已超过结构设计规定的承载极限88 MPa.因此，需要对初始设计方案进行重新设计，以使减振器座结构的承载应力降到许用应力目标值以下.本文采用拓扑优化设计方法，以期找到合理的减振器座承载受力结构，具体的拓扑优化实现过程包含以下几个内容.

图2 减振器座初始设计方案Von.Mises应力云图

2.1 定义拓扑优化设计区域并创建有限元模型

通常在拓扑优化前要根据结构安装、受载情况定义其优化设计域空间，即设计变量的变化范围.在此定义减振器座的优化定义域空间相对减振器座的结构位置如图3所示.优化时通过对红色设计域空间中材料(单元)的删减实现材料密度在0～1之间的变化，从而最终得到设计域空间材料的分布状况.图中左侧方槽和中间两个方孔为预留螺栓安装空间，为非设计空间，不允许改动，计算过程中此区域中的材料(单元)密度不发生变化，始终为1.

图3 拓扑优化设计区域及有限元模型

2.2 定义目标函数、约束条件及设定参数

拓扑优化中的目标函数和约束函数都需要从有限元分析中获得相应的结构响应值.本文共定义了3个响应:质量、位移和应力，其中以位移和应力响应作为约束，以质量最小为设计目标.另外，通过定义最小成员尺寸控制消除结果中的细小传力路径，保证优化中结构最小尺寸大于最小成员尺寸，以得到均匀的材料分布;定义棋盘格参数和离散参数消除中间密度单元或交错单元的产生，以获得合理优化结构，并保证制造工艺实施的便捷;定义脱模方向，保证刀具的进出方向.在此将棋盘格参数设定为1，最小尺寸参数设定为3，离散参数设定为3，通过以上设定得到的材料密度分布如图4所示.

图4 材料密度分布云图

2.3 优化结果处理及计算验证

图5 拓扑优化所得减振器座三维实体模型

图6 拓扑优化所得减振器座结构Von.Mises应力云图

求解得到上述材料密度分布后，通过hyperworks中的ossmooth工具将拓扑图中密度值为0.3的等值面输出为igs格式文件，并导入三维建模软件中进行人工修正，以得到易铸造和加工的最终方案模型.如图5所示，所得优化结构的模型质量为30 kg，相比初始设计结构方案，结构减重24.3%.将优化得到的结构方案导入有限元软件中重新进行求解计算，计算结果显示，优化后得到的结构方案的最大Von.Mises应力值为67.89 MPa，在结构的承载许用Von.Mises应力值88 MPa以下，如图6所示.消除了初始设计结构在悬臂根部的局部应力集中，并通过优化设计调整材料的分布使应力分布均匀合理，降低了最大应力值，从而降低了产生疲劳裂纹的风险.另外，优化后的结构在保证了刚度要求条件下，减重24.3%，提高了材料使用率，降低了生产成本.

3 结论

(1)利用拓扑优化设计方法，可以为结构寻找最优的材料分布形式，尤其在结构的概念设计或方案修改中，能够缩短设计周期，提高设计品质;

(2)拓扑优化后的结果需进行一定的光滑处理或局部修改，以满足工程化制造的需要;

(3)从最后的优化结果来看，基于拓扑优化方法得到的结构是合理的受力承载结构，即该优化方法有效;

(4)结构优化设计虽已在许多方面取得成果，但由于拓扑优化设计内容涉及到多学科，在今后的工程应用中还需要进行较为深入的研究.

［1］耿楷真，马国伟，潘树国.结构优化方法及其在舰载武备结构设计中的应用［J］.舰船科学技术，2007，29:134-137.

［2］杨树凯，朱启昕，吴仕赋.基于有限元技术的汽车支架拓扑优化设计研究［J］.设计·计算·研究，2006(3):16-18.

［3］张胜兰，郑冬黎，郝琪，等.基于HyperWorks的结构优化设计技术［M］.北京:机械工业出版社，2007.

［4］王凌.智能优化算法及其应用［M］.北京:清华大学出版社，2001.

［5］玄光男，程润伟.遗传算法与工程优化［M］.北京:清华大学出版社，2004.

［6］解可新.最优化方法［M］.天津:天津大学出版社，2004.

［7］钱令希.工程结构优化设计［M］.北京:水利电力出版社，1983.

［8］聂春戈，李晓峰，兆文忠.高速转向架轴箱转臂结构拓扑优化设计［J］.机械设计，2007，24(6):58-60.