大学测量学教材中水准测量原理的改进

邓永和

(丽水学院建筑工程系,浙江丽水 323000)

1 传统的水准测量原理

我国几乎所有的大学测量学教材中,水准测量原理都存在问题。

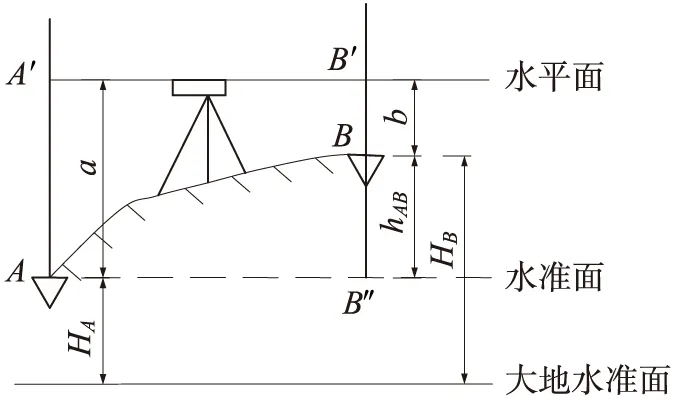
图1 传统的水准测量原理

在图1中,设A、B两点的高程依次为HA、HB,两点标尺的读数依次为a、b,A、B两点的高差为hAB,于是,我国几乎所有的大学测量学教材[1～8]就直接武断地写出

hAB=a-b

(1)

这就是它们认为的水准测量的原理。其实,这是错误的。在图1中,假设水准仪提供的水平视线与A、B两点处铅垂的标尺交于A′、B′,虽然A′、B′在同一水平面上,但不一定在同一水准面上,因此,A′、B′两点的高程不一定满足

HA′=HB′

(2)

过A点的水准面与B点处标尺交于B″,即A、B″在同一水准面上,那么,A、B″两点的高程满足

HA=HB″

(3)

根据高差与高程的关系

hB″B′=HB′-HB″

(4)

hAA′=HA′-HA

(5)

再顾及前面的HA=HB″,以及HA′和HB′不一定相等,因此

hB″B=hAA′

(6)

不一定成立,即下式

b+hAB=a

(7)

不一定成立,也就是等式(1)不成立,这就证明了传统水准测量原理是错误的。上面是根据hAB为正时得到的结论。当hAB为负时,也可以得到相同的结论。

2 改进的水准测量原理

前面已经证明传统的水准测量原理是错误的,为了水准测量理论的完善和测量学教材的更正,因此,有必要推导出正确的水准测量原理。

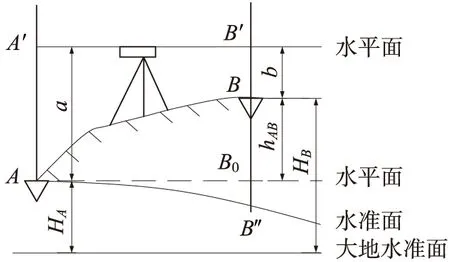
图2 改进的水准测量原理

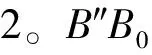
(8)

显然,四边形A′AB0B′是矩形,对边相等,即下式

(9)

成立,也就是

(10)

成立,于是得到

(11)

hAB=a-b

(12)

上式推导思路与公式(1)的思路完全不同。前面是根据hAB为正时得到的结论。当hAB为负时,也可以得到相同的结论。

3 结束语

(1)本文严密证明了我国大学测量学教材的水准测量原理存在错误,并推导了正确的水准测量原理,对于水准测量理论的完善和测量学教材的更正都具有积极的意义。

(3)由于水准测量原理存在问题,因此,本文对于采用水准仪做变形监测与预报,以及水准仪的常规维修等,都是具有一定的积极意义的。

(4)笔者在这里针对水准测量的原理抛砖引玉,希望引起测绘界的深思。

[1]陈丽华.测量学[M].杭州:浙江大学出版社,2009

[2]顾效烈,鲍峰,程效军.测量学(第三版)[M].上海:同济大学,2006

[3]李天文.现代测量学[M].北京:科学出版社,2007

[4]覃辉主编.土木工程测量(第三版)[M].上海:同济大学,2008

[5]罗志清.测量学[M].昆明:云南大学出版社,2006

[6]付新启.测量学[M].北京:北京理工大学出版社,2006

[7]潘延玲主编.测量学[M].北京:中国建材出版社,2001

[8]熊春宝,伊晓东.测量学[M].天津:天津大学出版社,2007