基于SMI-LMS的自适应旁瓣干扰抑制算法研究*

何永华，贾 鑫，高 阳

(装备学院 光电装备系，北京 101416)

1 引言

自适应旁瓣干扰抑制是雷达抑制有源旁瓣干扰的有效措施，具有强的抗干扰能力，目前采用较多的算法有LMS、RLS和SMI算法等，且有许多的改进算法。文献［1］提出一种LS-LMS算法，首先利用小快拍数LS算法计算加权矢量，其次用此加权矢量作为LMS算法的初始加权矢量，再次利用传统的LMS算法对加权矢量进行更新。通过仿真实验验证了该方法具有计算量小、收敛速度快、收敛性能对初始值不敏感且收敛速度与干扰环境无关的特点。

本文提出一种基于SMI-LMS的自适应旁瓣干扰抑制算法。SMI(采样矩阵求逆）算法利用雷达工作的休止期采集干扰噪声数据样本，并估计干扰噪声协方差矩阵，以此直接计算权值，具有收敛速度快的优点。SMI-LMS算法利用SMI算法在低快拍下的权值作为LMS算法的初值进行迭代，解决了SMI算法运算量大和LMS算法不易收敛的问题。文章分别从方向图增益和运算量等方面对两种算法进行比较分析，最后运用对角加载技术对SMI-LMS算法作了改进。

2 算法原理分析

设有一均匀线阵，阵元数为N，假设每个阵元各向同性，忽略通道不一致性和互耦的影响，阵列接收信号为x(n），阵列加权矢量为w(n），则阵列输出为

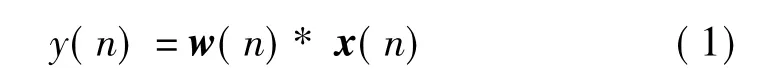
自适应算法的核心即是加权矢量w(n）的计算方法，不同算法获得权矢量的方法也不相同。

2.1 LS-LMS算法［1］

LMS算法是基于参考信号的闭环算法，通过使参考信号与加权相加的阵列输出之差的均方值最小调整阵列自适应加权矢量。假设参考信号为d(n），阵列输出误差为e(n），则有

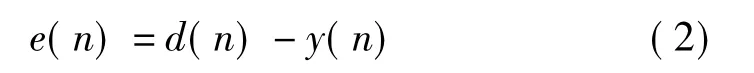
LMS算法是使e(n）的均方值最小化，其代价函数为

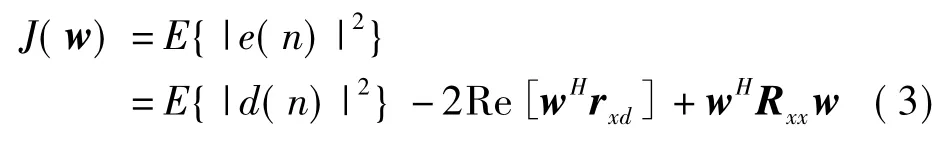
式中，E{ } 表示统计平均，Re 表示取实部，Rxx=E{ x(n）xH(n）}为输入矢量的自相关矩阵，rxd=E{x(n）d*(n）}为输入矢量x(k）与期望信号d(k）的互相关矩阵。

LMS算法的权矢量更新公式为

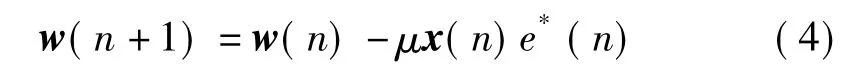
其中μ 是步长因子，LMS算法的收敛与初值和步长均有关系。

LS算法是一种开环算法，其代价函数为

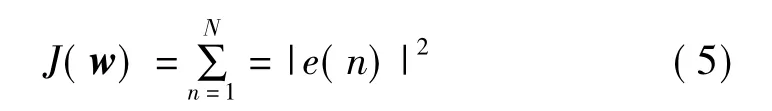
式中N为快拍数。

令代价函数的梯度为零，得到最小二乘方法的最优加权矢量:

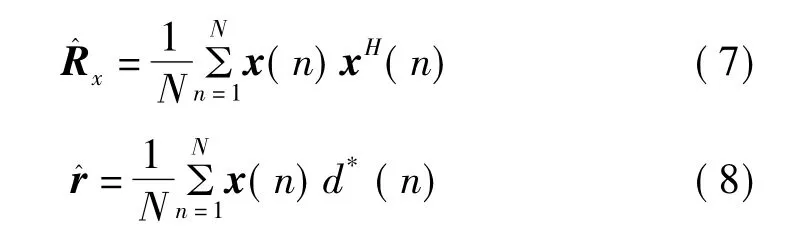
从上式可以看出LS算法的求解较复杂，除了要求解自相关矩阵、互相关矢量外，还要进行矩阵求逆运算，具有很大的运算量。

文献［1］通过对上述两种算法分析提出LS-LMS算法。该算法用LS算法在小快拍数时计算出的加权矢量作为LMS算法的初始值，然后再利用LMS算法进行权值更新。

2.2 SMI-LMS算法

SMI算法根据估计的采样协方差矩阵求逆直接计算权矢量，该算法满足最大信干噪比准则［2］:

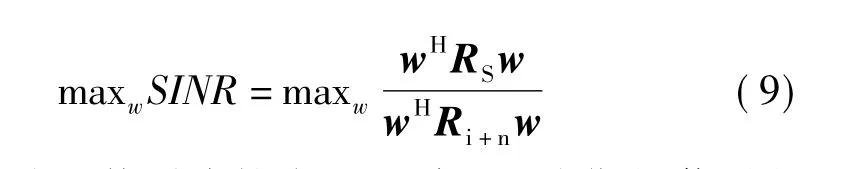
式中Ri+n即为干扰噪声协方差矩阵，RS为期望信号的自相关矩阵，w为权矢量。其最优权矢量表达式为［2］

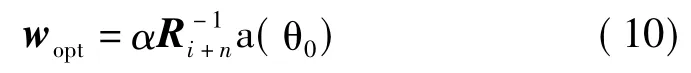
式中Ri+n为干扰噪声协方差矩阵，a(θ0）为期望信号的导向矢量。

实际上，信号、杂波和干扰环境往往是先验未知的，Ri+n的准确值无法得到，只能通过采样数据得到其最大似然估计［3-4］:

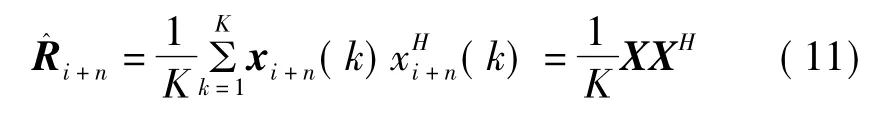
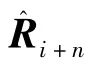
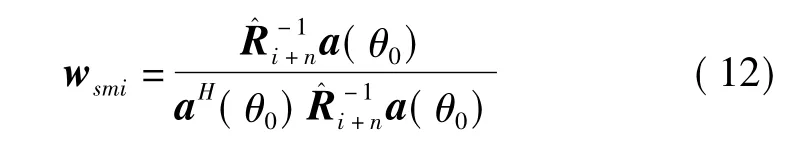
该算法在快拍数较多时要进行自相关矩阵的估计和矩阵求逆运算，同样具有很大的计算量，不利于算法的实时实现。

文章提出的SMI-LMS算法，利用了两种算法的优点，在低快拍数据下，由SMI算法计算出权值，并以之作为LMS算法的初始权值，通过不断迭代进行权值更新。

首先利用低快拍数据得到SMI算法下的权值［2］:

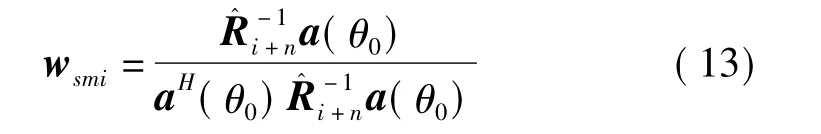
以此作为LMS算法的初始取值，然后再利用LMS算法进行权值更新。

对于阵元数多的阵列天线，快拍数的增加必然增加运算的复杂性，并且如系统利用工作的休止期采集干扰噪声数据样本，由于间歇时间已知，可得到的采样数据是有限的。因此，SMI算法利用低快拍数据计算初始权值，再由LMS算法进行权值更新是能够提高系统工作性能的。

3 改进SMI-LMS算法

雷达利用其工作的休止期采集干扰噪声数据样本，由于间歇时间已知，可得到的采样数据是有限的。因此，对协方差矩阵的估值与真实值之间会存在误差，引起特征值的扩散，进而导致自适应波束畸变，严重影响波束的副瓣性能。

对阵列天线干扰噪声估计不足会造成协方差矩阵特征值分散。通过对角加载，选择合适的加载值，则对应于强干扰的大特征值不会受到很大影响，而与噪声相对应的小特征值被加大并压缩在加载值附近［5］。

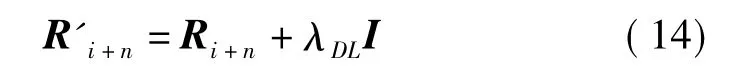
式中，λDL为加载值，I为单位阵。

对角加载是一种有效的改善自适应波束性能的方法［3］，采用对角加载的方法可以减少采样协方差矩阵特征值的扰动，从而可以实现在较少快拍数的采样条件下改善自适应波束的旁瓣性能，有效地抑制干扰。此处，利用对角加载方法产生的权矢量更接近最优值。

4 算法复杂度分析

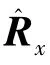
设N为阵元数，K为快拍数，M为两种算法中计算初始权矢量的快拍数，其中M＜＜K。则LS-LMS算法的复数乘法运算量可表示为［1］

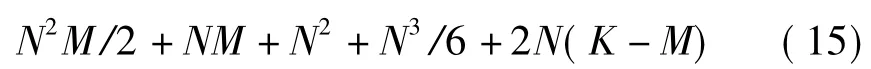
SMI-LMS算法的复数乘法运算量可表示为

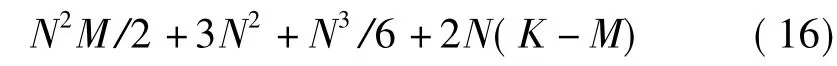
改进的SMI-LMS算法只是协方差矩阵加上对角阵，属于附属加法，对总的运算量影响不大，因此与SMI-LMS算法的运算量基本相同。

通过式(15）、(16）比较可以看出，两种算法的复数乘法运算量基本一致，均与阵元数和快拍数直接相关。在阵元数N和快拍数M 增大时，运算量将迅速增大。由上式可以看出，采用小快拍数计算初始取值的方法，由于M＜＜K，使得运算量大大减少，同时初始权值接近最优，将加快收敛速度。

5 仿真实验

为验证上述算法分析的正确性，并对比分析不同条件下算法的性能，本文对上述原理作了如下的仿真验证。

5.1 LS-LMS与SMI-LMS算法的对比分析

采用阵元数N=8 均匀线阵，阵元间距为波长的一半，期望信号入射方向为0°，信噪比为2 dB，干扰信号入射方向为45°、18°和－35°，干噪比分别为15 dB、20 dB和30 dB。

图1为分别取初始快拍数K为12、24和48 下LSLMS和SMI-LMS算法的波束方向图增益对比，虚线为LS-LMS算法，实线为SMI-LMS算法。可以看出，两者都能在干扰方向上形成很深的零点，且在不同快拍数下方向图增益基本一致，并随着快拍数的增多，副瓣电平抑制较好，方向图得到改善。

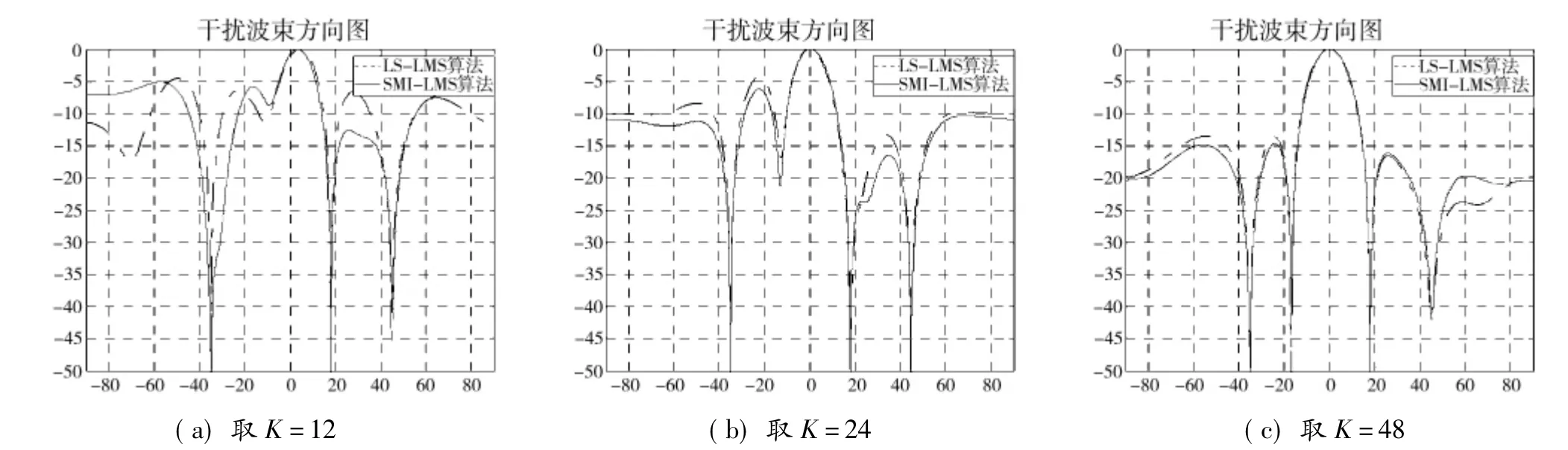
图1 LS-LMS与SMI-LMS波束方向图比较

5.2 改进SMI-LMS算法

根据上述分析，SMI算法在采用对角加载技术时，低快拍下的波束方向图旁瓣性能得到改善。与上次实验条件相同，将改进的SMI-LMS算法与LS-LMS算法进行对比分析，分别取初始快拍数K为12、24和48，如图2所示。

由图2 可知，采样对角加载技术的SMI-LMS算法所形成的波束方向图较为稳定，且副瓣较低，随着快拍数的增加，LS-LMS算法的波束方向图增益渐与之趋于一致，说明在低快拍下改进SMI-LMS算法显示出好的性能。

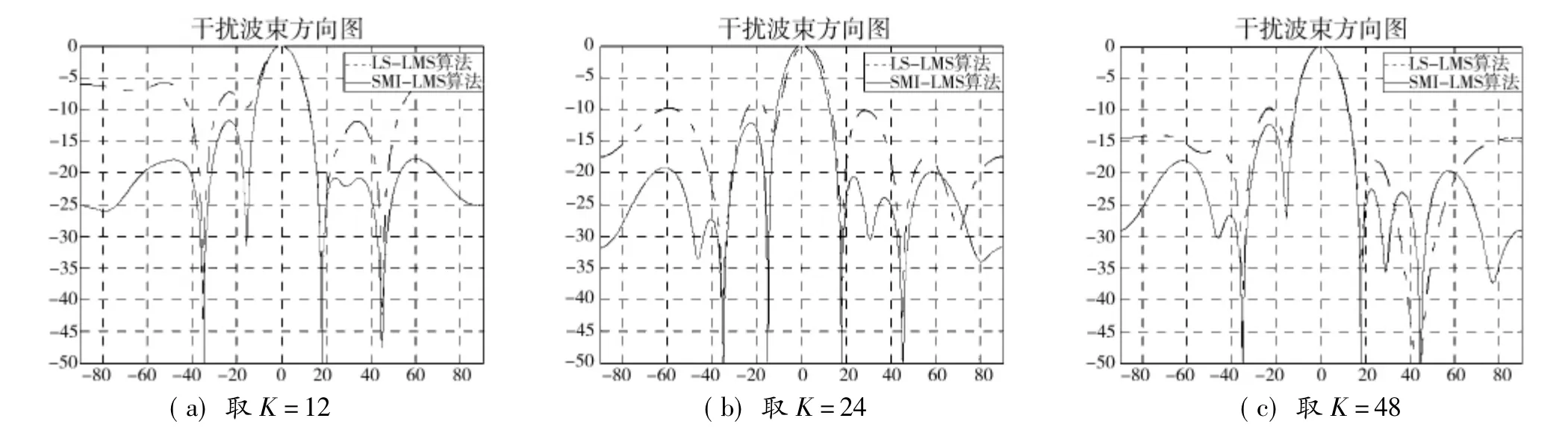
图2 LS-LMS与改进SMI-LMS算法比较

5.3 算法性能仿真分析

如下是从SINR 损失的角度对该改进算法的性能进行对比分析，仿真条件不变，定义输出信干噪比损失为算法下的输出信干噪比与最优输出信干噪比的比值［2，6］:

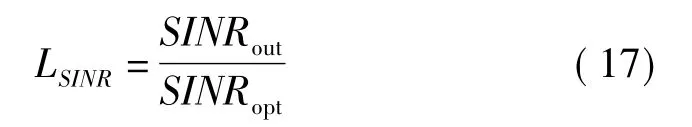
式中SINRopt为阵列最优权矢量对应输出信干噪比，SINRout为有限快拍数据下算法对应的输出信干噪比，SINRout越小，即性能越差，LSINR越小。

对比分析LS-LMS、SMI-LMS 及改进SMI-LMS算法下阵列输出信干噪比损失曲线，可以看出，随着快拍数的增加，算法对应的输出信干噪比逐渐趋于最优，但在低快拍下，改进SMI-LMS算法输出信干噪比更大，性能更好。

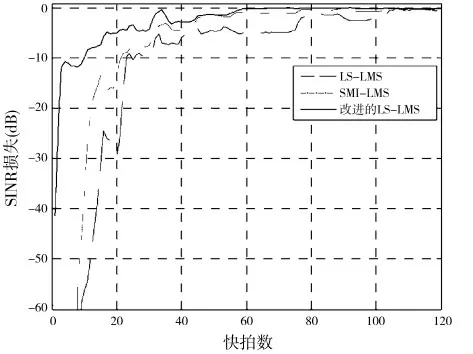
图3 不同算法下输出信干噪比损失对比曲线

6 结束语

本文首先分析研究了文献［1］提出的LS-LMS算法，并提出SMI-LMS算法，以小快拍数据SMI算法计算出的权矢量作为LMS算法的初始加权矢量，能够获得较为理想的波束方向图增益。通过仿真分析可知，该算法性能与LS-LMS算法类似，并且两种算法的复杂度基本一致。采用对角加载技术对SMI-LMS算法进行改进，仿真分析可知，在低快拍下改进的SMI-LMS算法有着更好的性能。

［1］石庆研，钟伦珑，吴仁彪.基于LS-LMS的智能天线自适应干扰抑制方法［J］.信号处理，2010，26(5）:677-681.

［2］王永良，丁前军，李荣锋.自适应阵列处理［M］.北京:清华大学出版社，2009.

［3］刘桂瑜，廖桂生，陶海红.一种小快拍情况下的稳健的波束形成方法［J］.火控雷达技术，2008，37(1）:23-27.

［4］龚耀寰.自适应滤波(第二版）［M］.北京:电子工业出版社，2003.

［5］廖洁，陈洪.一种波束形成中的自适应对角加载方法［J］.通信对抗，2006(5）:14-17.

［6］沈福民.自适应信号处理［M］.西安:西安电子科技大学出版社，2001.