静水压力下变厚度圆柱（锥）壳结构强度分析

王永军，万正权，沈永春

（中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

现代潜艇均包括多个不同功能的舱段，彼此间通过连接结点进行连接。对于结构尺度相差较大的舱段进行连接，其连接结点也必须特殊设计，如“厚板削斜连接”[1-2]、“锻钢环连接”[3]、“锥—环—柱连接”[4-5]等等。这些结构可以有效减缓结构的应力集中，同时有效降低结构重量。即便如此这些连接结点区域仍然是潜艇耐压结构的高应力区，必须对其在静水压力下的强度进行准确分析。

对这些连接结点进行观察可以发现，它们可以分解为等厚度柱（锥）壳、变厚度柱（锥）壳等基本结构。等厚度圆柱壳结构求解相对简单，利用克雷洛夫函数可以进行精确求解[6]。对于等厚度圆锥壳也存在解析解[7]或准确解[8]，但需使用Besse函数等高等函数，数学处理过程较为复杂。变厚度圆锥壳更加复杂，其平衡方程包括两组变系数，进行精确求解更为困难。本文作者在文献[9]中利用幂级数法建立了一种简化的等厚度圆锥壳结构强度解析方法。本文将在文献[9]研究的基础上，将其推广到线性变厚度圆锥壳上，利用幂级数法推导其壳单元刚度阵及载荷阵，建立可以对变厚度强度进行准确分析计算的解析单元法（Analytic Element Method,AEM）。

2 变厚度圆柱（锥）壳单元

在文献[9]圆锥壳平衡方程的基础上，推导考虑大挠度效应的线性变厚度圆柱（锥）壳单元的刚度矩阵与载荷列阵。线性变厚度圆柱（锥）壳单元包括两个节点四个自由度。当壳体的母线为曲线或厚度为非线性变化时，可以利用为多个变厚度圆柱（锥）壳单元进行近似分析，因而该单元具有更大的通用性。

变厚度圆柱（锥）壳单元简图、单元坐标系及变形与载荷方向见图1，假设静水压力始终垂直作用于壳体中面。

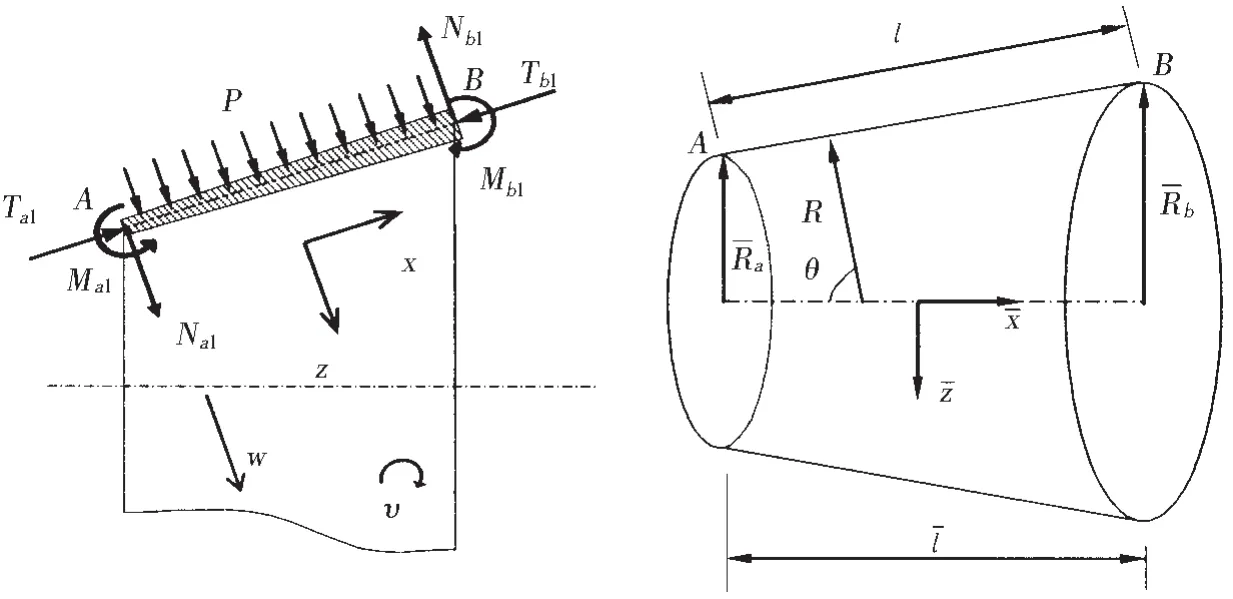
图1 变厚度圆柱(锥)壳单元结构简图与坐标系Fig.1 Sketch and element coordinate system of cone shell with varible thickness

2.1 变厚度圆柱（锥）壳平衡微分方程

根据变厚度圆柱（锥）壳结构特点，可得如下方程组：

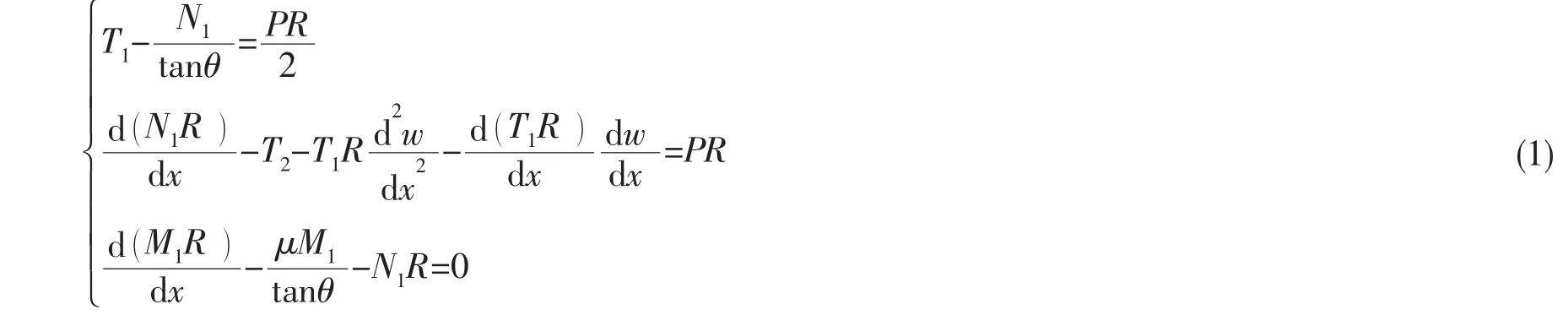
由于厚度与主曲率半径均为线性变化，因此它们可以用母线坐标表示为：

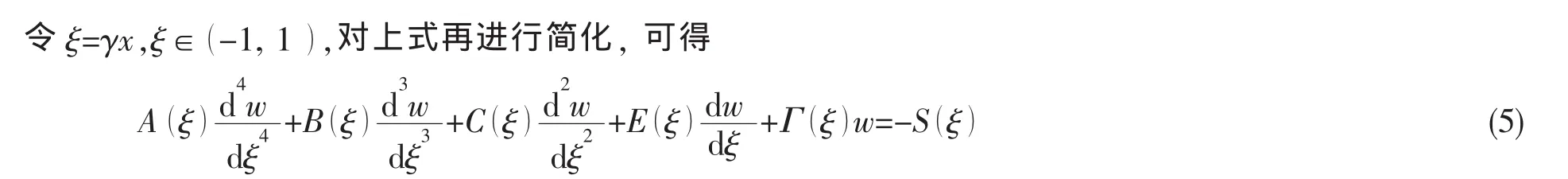
上式中所有系数均为幂函数，表达式如下：

2.2 平衡微分方程的解

2.2.1 齐次微分方程的幂级数解

方程（5）对应的齐次方程为：

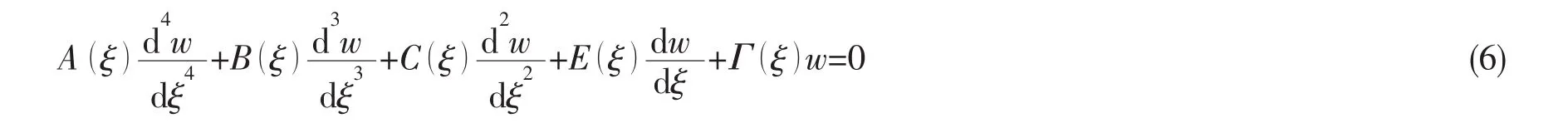
该方程的通解可以用幂级数进行如下表示：上式的一到四阶导数分别为：

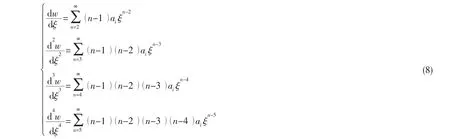
将（7）、（8）式代入（6）式可得

当n≤9时有

当n≥10时有

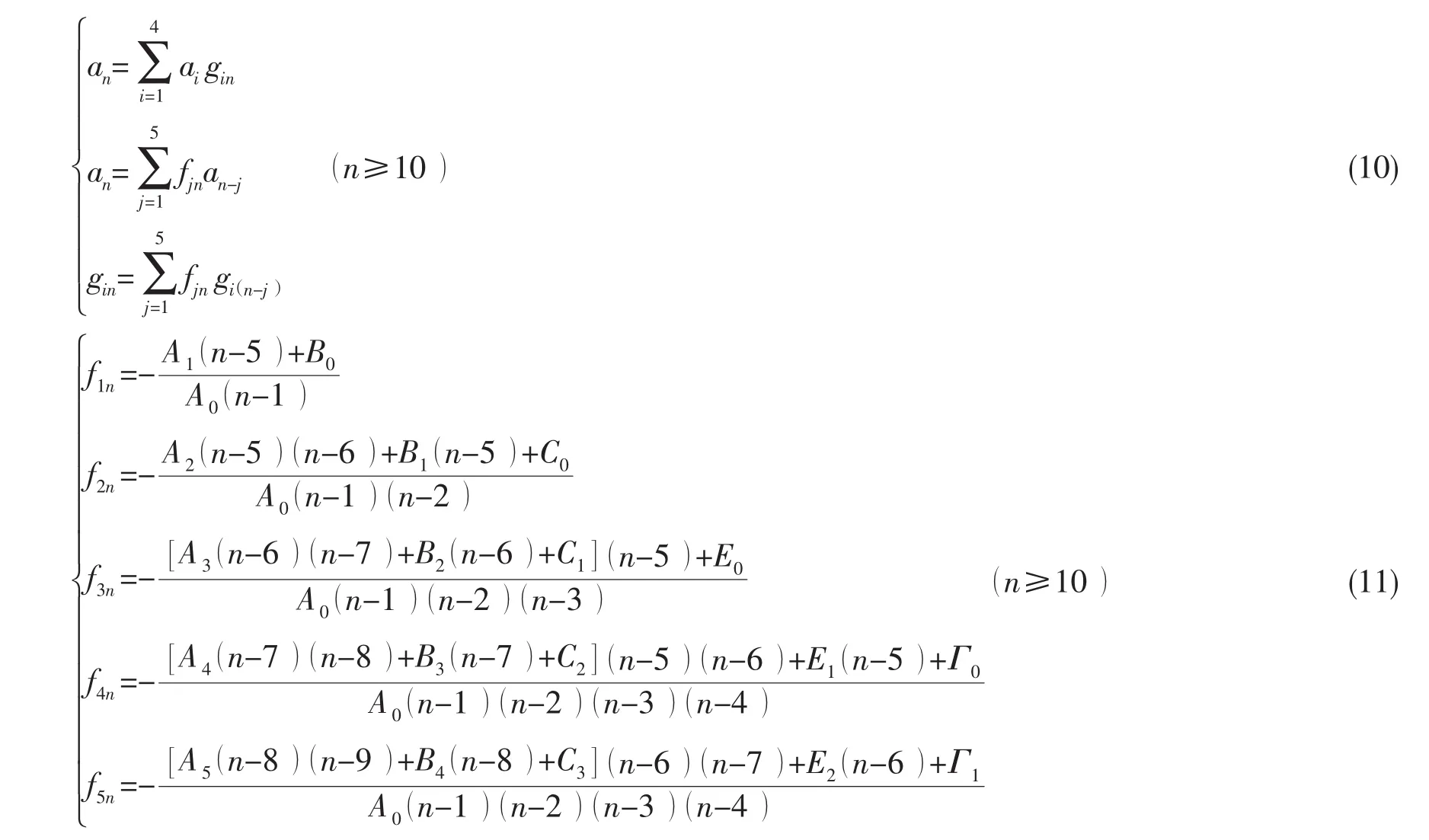
2.2.2 级数收敛性证明

下面对微分方程变量ξ定义域区间（-1,1）内的收敛性进行证明：

首先，确定（7）式的收敛半径R，R=X

由（10）、（11）式可得

将 A0、A1、A2、A3、A4、A5表达式代入上式可得

由于λ1，λ2∈（-1，1 ），故由（13）式可得：

即（7）式的收敛半径R大于1，收敛区间为 ξ∈（-R，R），而微分方程的定义域 ξ∈（-1，1），显然在此收敛区间内，从而证明变厚度圆柱（锥）壳方程（6）可以利用幂级数法进行求解。

2.2.3 平衡微分方程特解

本节将利用伽辽金法确定边界为无矩状态时的非齐次方程特解。假定方程（5）在边界ξ＝±1上弯矩M=0，剪力N=0，方程的在无矩边界条件下的近似解及伽辽金权函数形式同[9]，此时残差函数为：该方程组中各系数项的表达式如下：

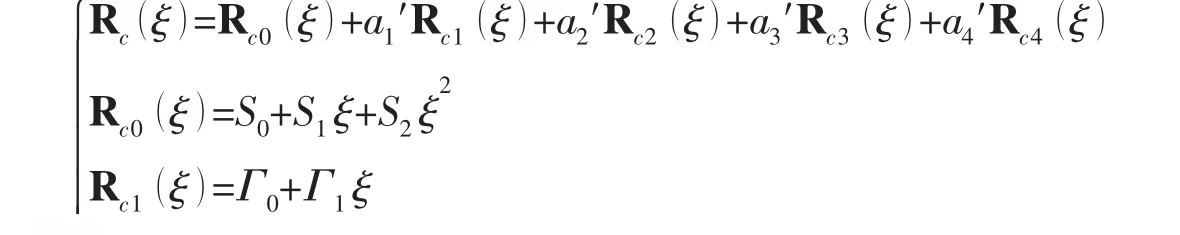
方程组（16）是关于 a1′、a2′、a3′和 a4′的四元线性方程组，对其求解即可得到 a1′、a2′、a3′和 a4′。 因此方程（5）的通解可以表示为：

利用（17）式即得变厚度柱（锥）壳结构各点的转角、弯矩与剪力的表达式：

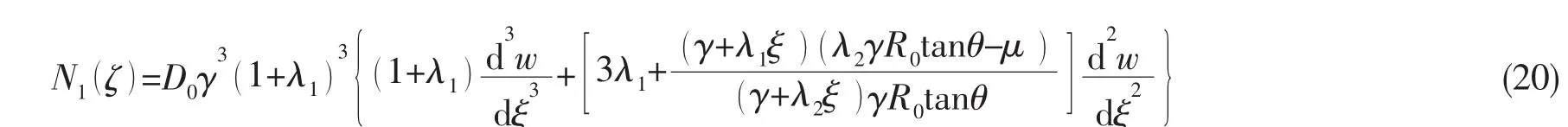
2.3 变厚度圆柱(锥)壳单元刚度矩阵与节点载荷列阵

2.3.1 节点位移

变厚度圆柱（锥）壳单元A、B节点位置分别为x=±l/2即ξ=±1，每个节点上各有径向位移、转角、弯矩和剪力四组量，其中径向位移、转角为节点广义位移，弯矩、剪力为节点载荷。静水压力下变厚度圆柱（锥）壳单元在节点处的径向位移与转角可以用矩阵表示为：

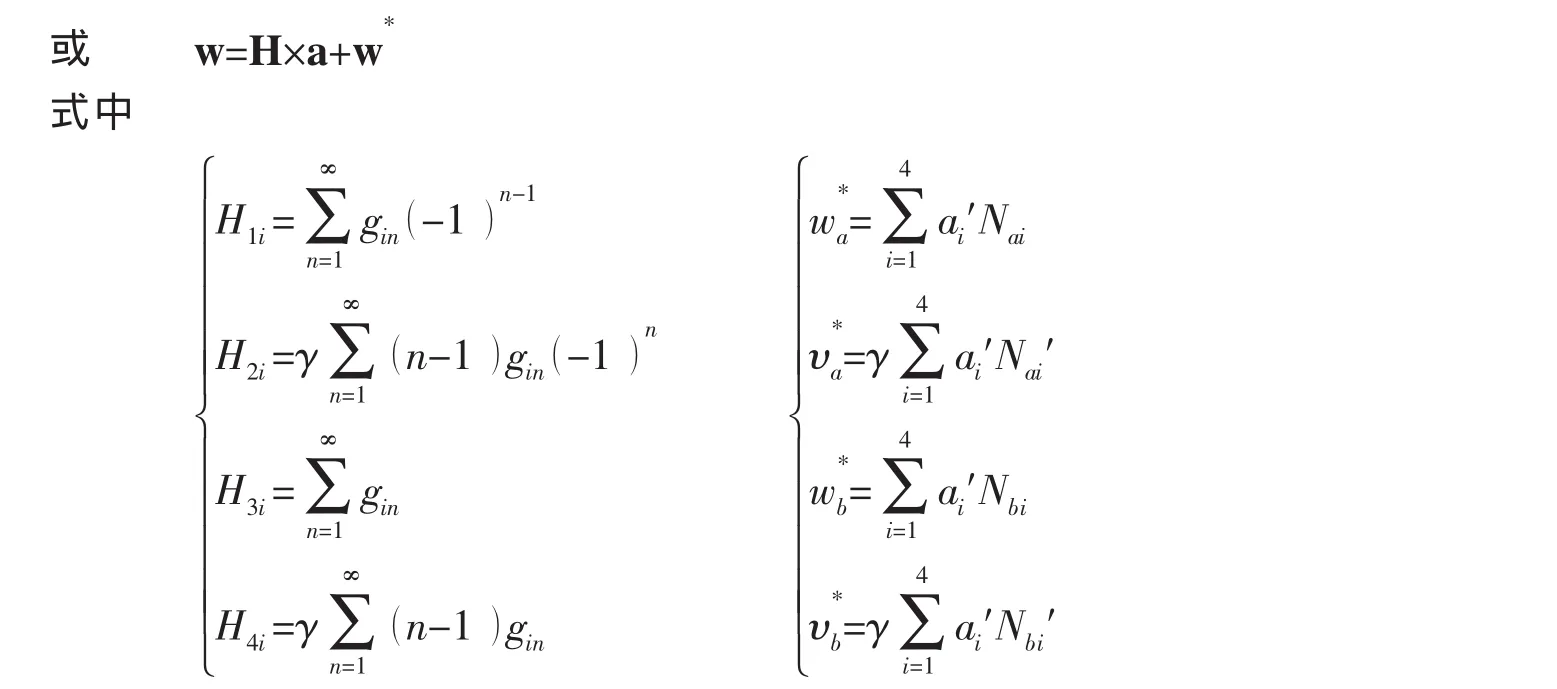
2.3.2 节点载荷

静水压力下变厚度圆锥壳结构在节点处的剪力与弯矩可以用矩阵表示为：

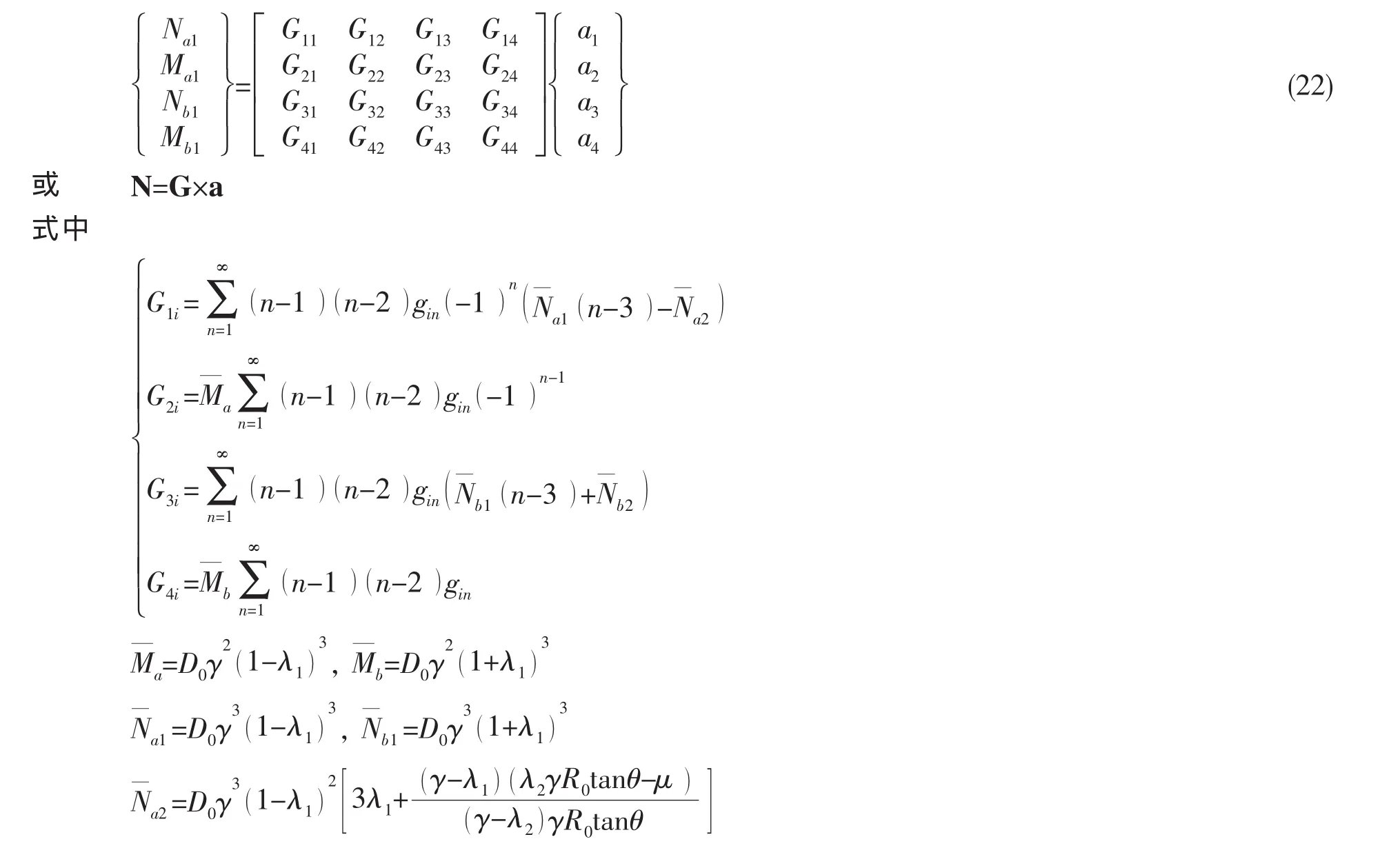
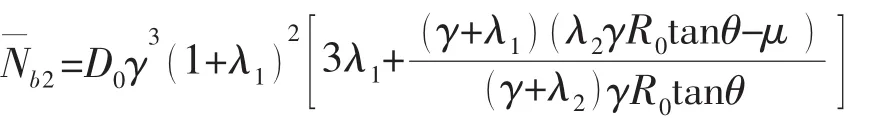
2.3.3 单元刚度矩阵与节点载荷列阵

将广义位移w转化到总体坐标系

将广义力N转化到总体坐标系

最终可确定二节点变厚度圆柱（锥）壳的刚度矩阵：

节点载荷列阵：

3 算例分析

本节将利用一只线性变厚度锥柱结合壳简化模型（见图2），通过与通用有限元法程序ANSYS10.0对比计算验证本文建立解析单元法对于锥—柱结合壳结构强度计算准确性，同时分析几何参数对该模型典型位置结构强度的影响。

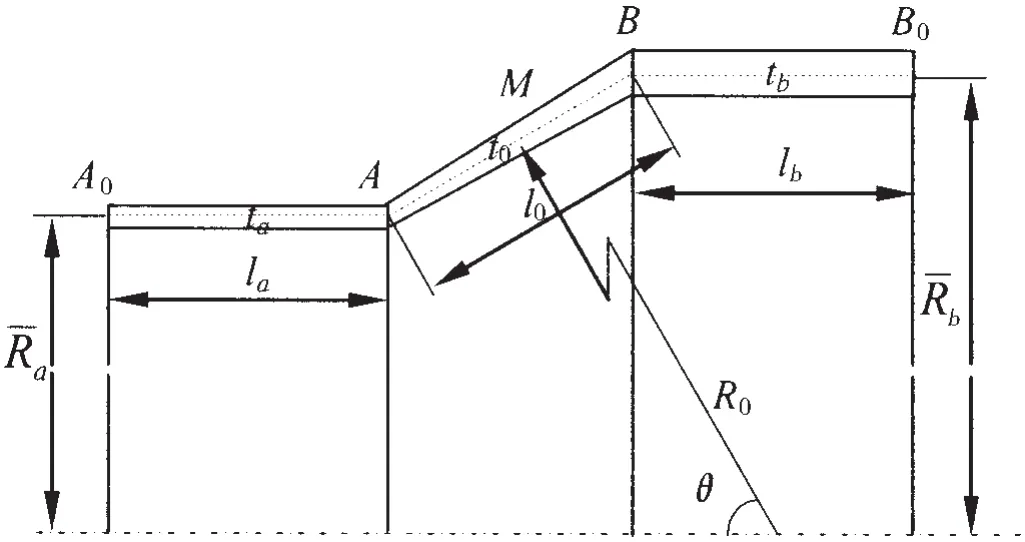
图2 变厚度锥柱结合壳结点简化模型Fig.2 Sketch of a simple cone-cylinder shell with varible thickness

计算模型锥壳中点M的主曲率半径R0=1 054mm，厚度为t0=8mm，母线长度为l0=180mm，法线与轴线夹角为60°。与锥壳相连的结构为等厚度圆柱壳，长度为la=lb=180mm，厚度等于与之相连的圆锥壳端A点与B点厚度，圆柱壳的另一端A0与B0施加简支边界条件。材料弹性模量E=1.96×105MPa，泊松比μ=0.3。在0.46Pcr计算压力下，保持M点厚度不变，通过调整厚度参数λ1改变锥壳的厚度变化，对该简化模型进行系列计算。利用解析单元法进行计算时级数取200项。实践表明级数项取15项以上即可获得较为准确的计算结果。ANSYS10.0通用有限元方法的网格尺度约为3t0，采用8节点壳体单元。

首先对参数进行无量纲化：

图3－5分别给出了λ2=0.189 5（θ=60°）时，锥壳小端根部A点中面周向应力系数KA2、外表面纵向应力系数KAt、内表面纵向应力系数KAb、随厚度参数λ1的变化规律。图6给出了锥壳中点M的中面周向应力系数KM2随厚度参数λ1的变化规律。图7－8分别给出了锥壳大端根部B点外表面纵向应力系数KBt、内表面纵向应力系数KBb、随厚度参数λ1的变化规律。

由这几组曲线可以发现，这几组应力系数AEM计算结果与FEM计算结果基本一致。在考虑大挠度效应与忽略大挠度效应两种情况下，系数KA2、KAt、KAb、KBt和KBb等最大偏差都在4%以下。考虑大挠度效应时系数KM2的最大偏差约为7%，此时λ1=0.5厚度差较大。因此，可以认为本文建立的变厚度圆（锥）壳强度AEM方法是准确可靠的。

由这几组曲线可以看出：应力系数KA2、KAt和KAb随λ1增大而增大，KAt、KAb随λ1增大而减少，KM2随λ1增加变化不显著。主要由于随厚度系数λ1的增大，A点厚度减薄，B点厚度增加，而M点厚度始终保持不变。

由图3-8中曲线还可以看出，对于这几组应力系数，大挠度效应影响明显，并且这种影响随λ1的增加越发显著。例如：当λ1=0时，如果考虑大挠度效应应力系数KA2将增加17%，当λ1=0.5时KA2将增加60%。应力系数KM2，不考虑大挠度效应时，KM2随λ1增加而增加，考虑大挠度效应后KM2随λ1增加而减少。

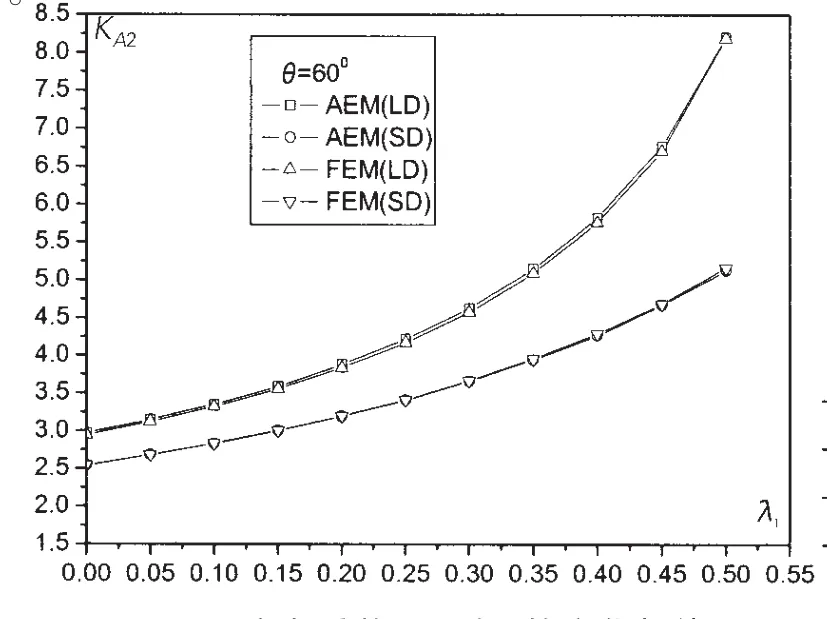
图3 应力系数KA2随λ1的变化规律Fig.3 Relationship between KA2and λ1

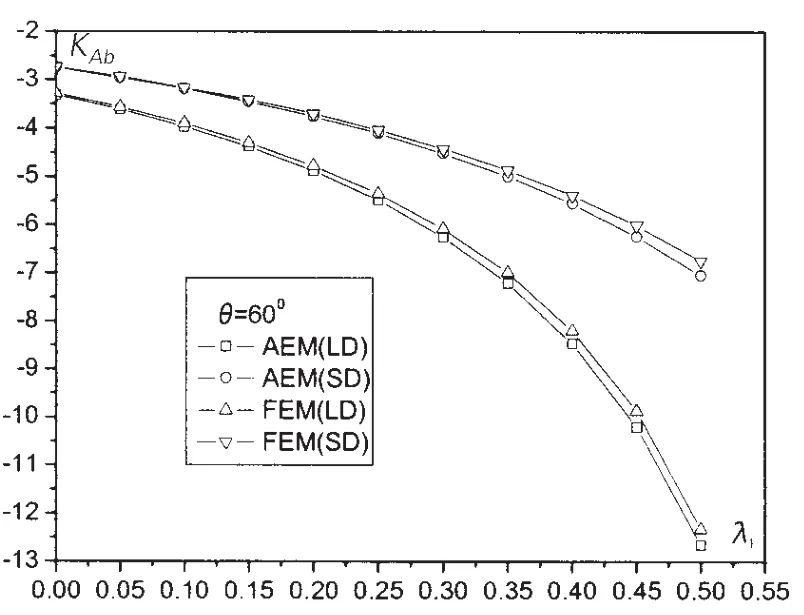
图4 应力系数KAb随λ1的变化规律Fig.4 Relationship between KAband λ1

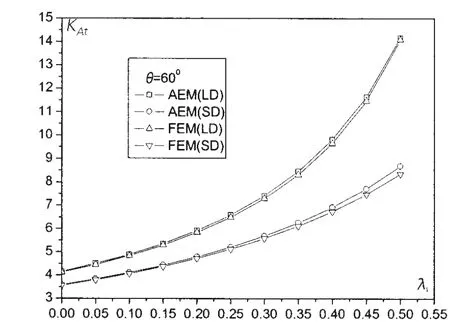
图5 应力系数KAt随λ1的变化规律Fig.5 Relationship between KAtand λ1

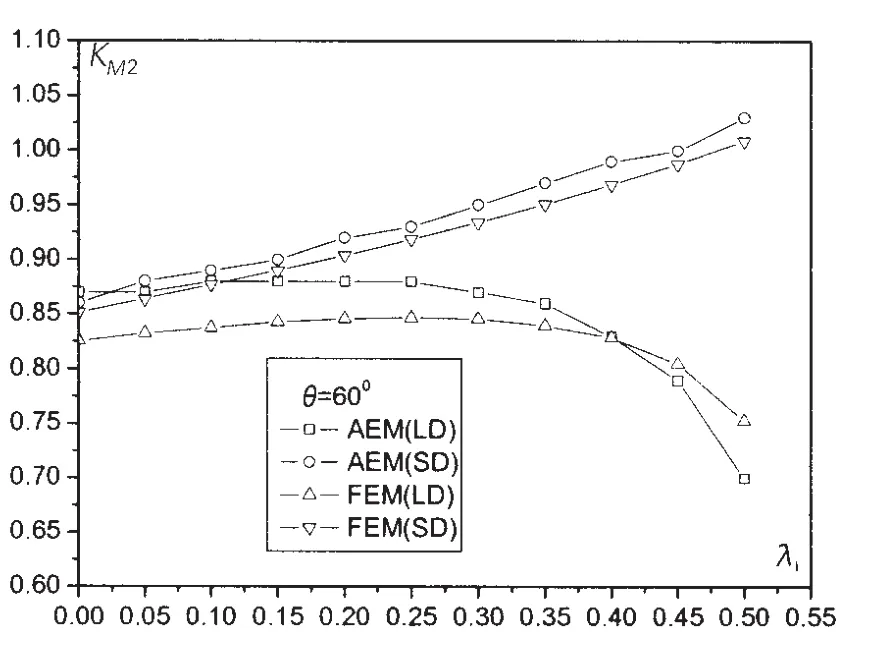
图6 应力系数KM2随λ1的变化规律Fig.6 Relationship between KM2and λ1

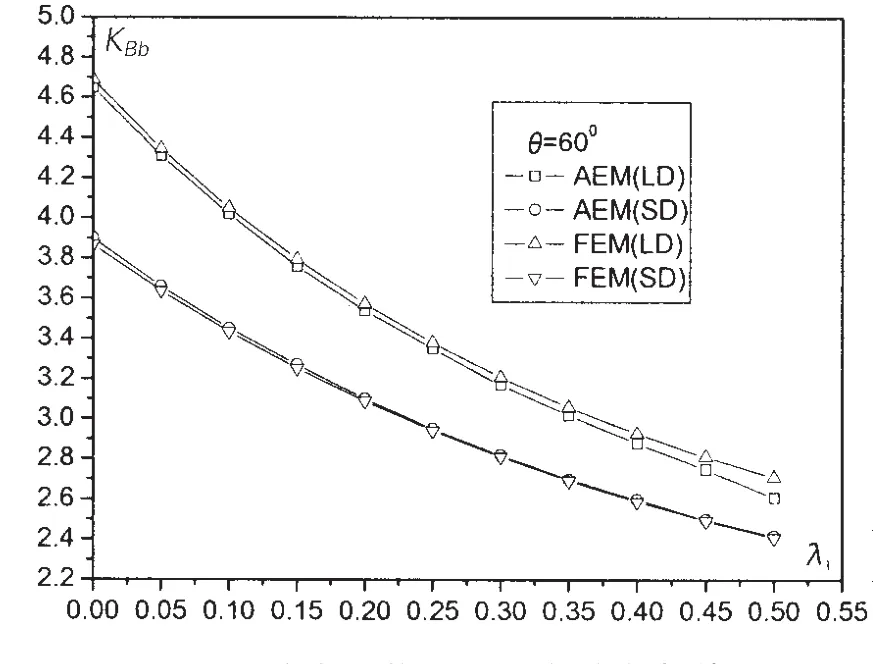
图7 应力系数KBb随λ1的变化规律Fig.7 Relationship between KBband λ1

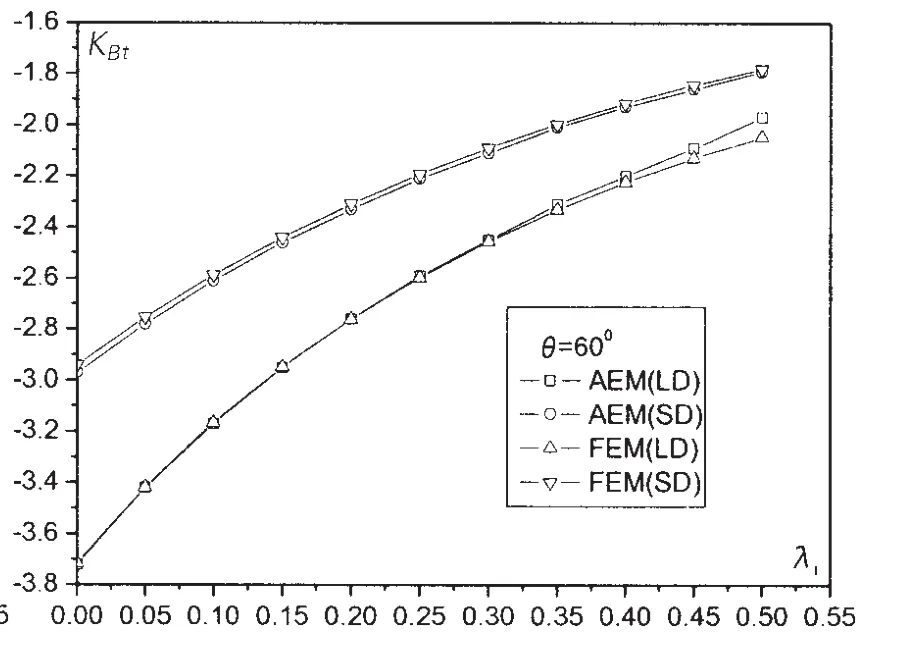
图8 应力系数KBt随λ1的变化规律Fig.8 Relationship between KBtand λ1

4 结 语

本文将变厚度圆柱（锥）壳简化为轴对称的二节点单元，根据平衡方法推导了该结构的单元刚度阵与载荷阵，建立了求解静水压力下变厚度圆柱（锥）壳结构强度的解析单元法（AEM）。利用该方法对一个简单的变厚度锥柱接合壳算例进行了计算并与有限元方法的计算结果进行了比较。研究表明，本文提出的AEM法可以对静水压力下变厚度锥壳结构强度进行准确分析。本文建立的方法可以推广到各种轴对称压力作用下的变厚度圆柱（锥）壳结构强度分析。

[1]蒋培林．带环肋加强的变厚度锥柱结合壳强度计算（迁移矩阵法）[J]．舰船科学技术,1984(12):24-35．

[2]蒋培林,宋学斌．潜艇锥柱结合壳加强形式研究[J]．舰船科学技术,1998(6):8-13．

[3]Raetz.Tichard V．An experimental investigation of small-scale conic reducer sections between cylindrical shells under external hydrostatic pressure[R]．DTMB,AD-650584,1960．

[4]黄加强,郭日修．分区样条等参元方法分析加肋轴对称组合壳[J]．计算力学学报,1998,15(1):58-68．

[5]黄加强,郭日修．加肋锥—环—柱组合壳强度及稳定性模型试验研究[J]．中国造船,1998(4):57-64．

[6]许辑平．潜艇强度[M]．北京:国防工业出版社,1980．

[7]А.Л.哥偿琴文塞尔著,薛振东等译．弹性薄壳理论[M]．上海:上海科学技术出版社,1963．

[8]裴俊厚,周殿邦,江 南．具有薄壳理论同样精度的圆锥壳的简化解[J]．舰船科学技术,2000(4):2-13.

[9]Wang Y J,Wan Z Q．Strength analysis of cone vessel under static pressure[J]．Journal of Ship Mechanics,2009,13(6):905-914．