冷弯薄壁钢类椭圆截面轴压构件设计方法

朱继华，辛佩龙，许 颖

(1.深圳大学 土木工程学院，518060 广东 深圳，zhujh@szu.edu.cn;2.深圳市立方建筑设计股份有限公司，518055 广东深圳;3.哈尔滨工业大学深圳研究生院，城市与土木工程学科部，518055 广东深圳)

冷弯薄壁钢类椭圆截面轴压构件设计方法

朱继华1，辛佩龙2，3，许 颖3

(1.深圳大学 土木工程学院，518060 广东 深圳，zhujh@szu.edu.cn;2.深圳市立方建筑设计股份有限公司，518055 广东深圳;3.哈尔滨工业大学深圳研究生院，城市与土木工程学科部，518055 广东深圳)

为研究冷弯薄壁钢空心类椭圆截面轴心受压构件的有限元数值模拟及设计方法，考察了现行冷弯薄壁钢结构设计规范中的有效宽度法对该类型截面构件的适用性.采用Abaqus建立冷弯薄壁钢空心类椭圆该模型可以准确地模拟此类构件的力学性能截面轴心受压构件的非线性有限元数值模型.有限元模型计算结果与试验结果的比较表明，该模型可以准确地模拟此类构件的力学性能.利用此模型进行了包括100个轴心受压构件的参数分析，参考现行的GB 50018—2002《冷弯薄壁型钢结构技术规范》及北美钢结构设计规范中的直接强度法计算以上构件的轴压承载力，并与试验和数值计算结果进行比较.结果证明直接强度法计算结果较准确，适用于此类构件的设计.

冷弯薄壁钢;轴心受压构件;有限元数值模拟;直接强度法

我国现行标准GB 50018—2002《冷弯薄壁型钢结构技术规范》［1］以及欧美等国标准中关于冷弯薄壁钢轴压构件的设计均采用有效宽度方法.有效宽度方法基于有效截面假定，将截面分割为板件并计算每一板件的有效宽度，对于截面形式发展越来越复杂的冷弯薄壁钢构件而言，采用有效宽度法进行设计非常繁琐.对于本文研究的空心类椭圆截面钢构件［2-3］(见图1)，需计算半圆板件的有效宽度并考虑半圆板件对相邻板件板阻约束系数的影响.然而，我国现行标准《冷弯薄壁型钢结构技术规范》中尚未提供相应的设计方法.近年来，国外科研学者以有限条法为基础提出了基于全截面分析的冷弯薄壁钢结构设计方法，称为直接强度法(DSM)［4］.该方法基于构件全截面来研究其屈曲强度，不必计算构件每一板件的有效宽度，基本克服了有效宽度法的不足.研究［5-7］表明，该设计方法对于常规的空心矩形、圆形和槽型截面构件均较为便捷和准确.然而，该方法是否适用于本文所研究的冷弯薄壁钢空心类椭圆截面构件还有待验证.

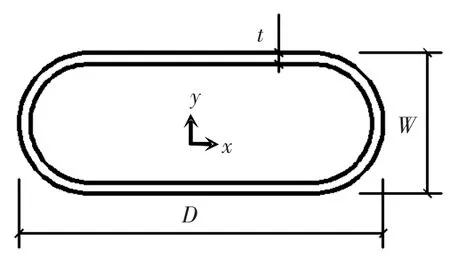
图1 截面尺寸定义

本文在28根冷弯薄壁钢空心类椭圆截面轴心受压构件试验的基础上，采用有限元分析软件Abaqus对此类构件进行了数值模拟和设计方法研究.基于试验和数值模拟结果，分别参照《冷弯薄壁型钢结构技术规范》及直接强度法设计公式计算了试验构件及数值模拟构件的轴压承载力，计算中根据试验情况对上述《冷弯薄壁型钢结构技术规范》中无法考虑的问题做出一定的假定.最后根据计算结果比较两种设计方法的计算精度，考察适用于此类构件的设计方法.

1 试验

Leung［8］报告了28根冷弯薄壁钢空心类椭圆截面轴压构件的试验结果.试验构件分为4个系列:W48T2、W38T2、W21T2.8 及 W15T1.6.各试验系列的名义截面尺寸和材性见表1.

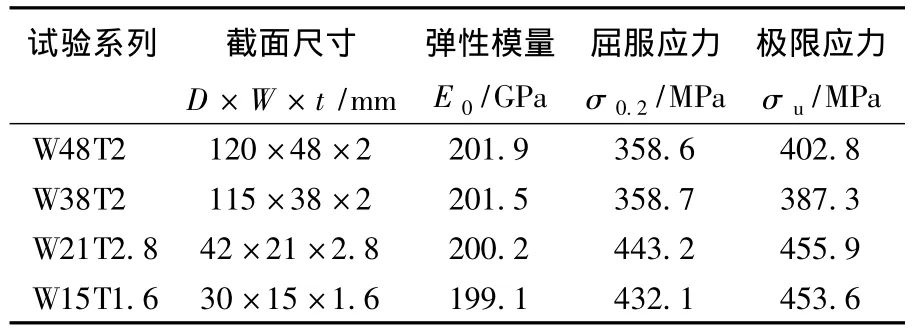
表1 试验系列的名义截面尺寸及材性

每个试验系列包括6～8根构件，长度变化范围为90～3 000 mm，对应的各系列构件最大长细比为75.5～131.6.构件编号规则为:第1部分为构件截面宽度，如 W48表示构件截面宽度为48 mm;第2部分为构件截面厚度，如T2表示截面宽度为2 mm;第3部分为构件的长度，如L360表示构件长度为360 mm;#表示重复的构件，如表2所示.各系列构件的材料本构关系由纵向拉伸试验获得，见表1.试验构件为两端固支，并通过焊接于构件两端的底板以位移控制模式加载，如图2所示.在试验前测量了长度大于360 mm的轴压构件的整体几何缺陷.试验获得的构件极限承载力及相应的破坏模式见表2.

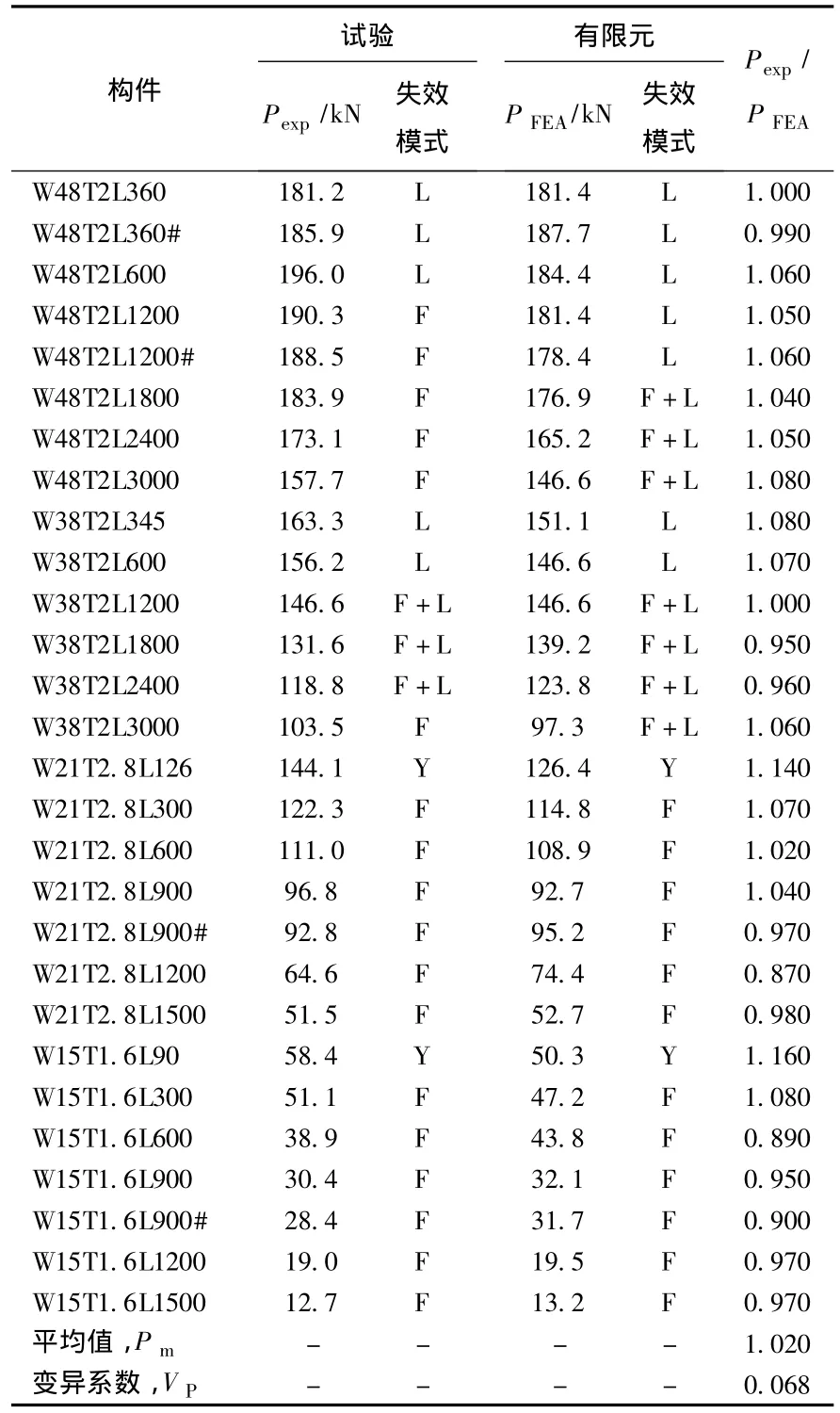
表2 试验结果与有限元模拟结果的对比

图2 试验装置图

2 有限元模拟

2.1 数值模型

采用有限元软件 Abaqus［9］建立了冷弯薄壁钢空心类椭圆截面轴压构件的非线性数值模型.模拟时考虑材料特性、边界条件以及初始几何缺陷，对构件进行非线性分析，得出有限元数值模拟(FEA)的极限承载力及失效模式.

模型采用Abaqus提供的S4R通用壳单元［9］，该类型单元已被证明可较好地模拟薄壁结构的力学性能［10］.FEA中材料的非线性本构关系由材料的真实应力 σtrue和真实 应 变 εture确定［9］，即σtrue= σ(1+ε)，εture=ln(1+ ε)－σtrue/E，其中工程应力σ、工程应变ε和初始杨氏模量E均通过纵向拉伸试验获得.数值模型采用的加载模式为位移加载，与试验采用的加载模式相同.边界条件为两端固支，柱的加载端除轴向自由度为自由外，其他方向的自由度均被约束.采用特征值分析方法考虑构件初始几何缺陷，基于FEA得到的轴压构件整体失稳和局部失稳变形曲线，将试验时测出的真实构件几何缺陷分配到模型的各结点.根据试验前测量的试验构件整体几何缺陷的平均值，数值模型构件的整体几何缺陷取为构件长度的1/1 500;局部几何缺陷取为构件厚度的10%［3］.

建模过程中比较了W48T2系列构件采用3种不同网格尺寸的数值模拟结果.根据比较结果，并基于计算精度和计算速度的综合考虑，选取W48T2、W38T2系列构件的网格尺寸为5 mm×5 mm，W21T2.8 及 W15T1.6 系列构件的网格尺寸分别为2.9 mm ×2.9 mm 和2.4 mm ×2.4 mm.

2.2 数值模型的校核

表2比较了FEA和试验得到的28个轴压构件极限承载力和破坏模式.W48T2、W38T2、W21T2.8 及W15T1.6 4个系列轴心受压构件的FEA模拟承载力PFEA与试验值Pexp相差较小，PFEA/Pexp的平均值Pm为1.02，变异系数 Vp为0.068;破坏模式与试验基本相同.图3为构件W38T2L600的试验和有限元模拟荷载-位移曲线对比.可见采用该模型模拟冷弯薄壁钢空心类椭圆截面轴压构件的极限承载力和失效模式较准确.

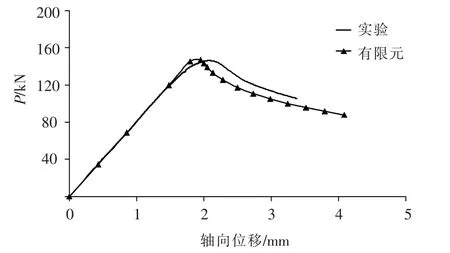
图3 W38T2L600轴向荷载－位移曲线

3 参数分析

该模型较准确地模拟了冷弯薄壁钢空心类椭圆截面轴压构件的极限承载力和失效模式，可采用此模型做进一步的参数分析.据此，采用该模型进行了20个系列共100个构件的计算.各系列截面尺寸如表3所示.构件编号规则与试验构件相同.每个系列包括500、1 200、2 000、2 700 和3 500 mm 5 个不同长度的构件.构件长细比变化范围为8～70，宽厚比变化范围为30～150.参数分析采用与前述数值模型相同的方法模拟初始几何缺陷、加载模式和材料本构关系，网格尺寸为10 mm×10 mm.参数分析得到的构件极限承载力PFEA详见表4.

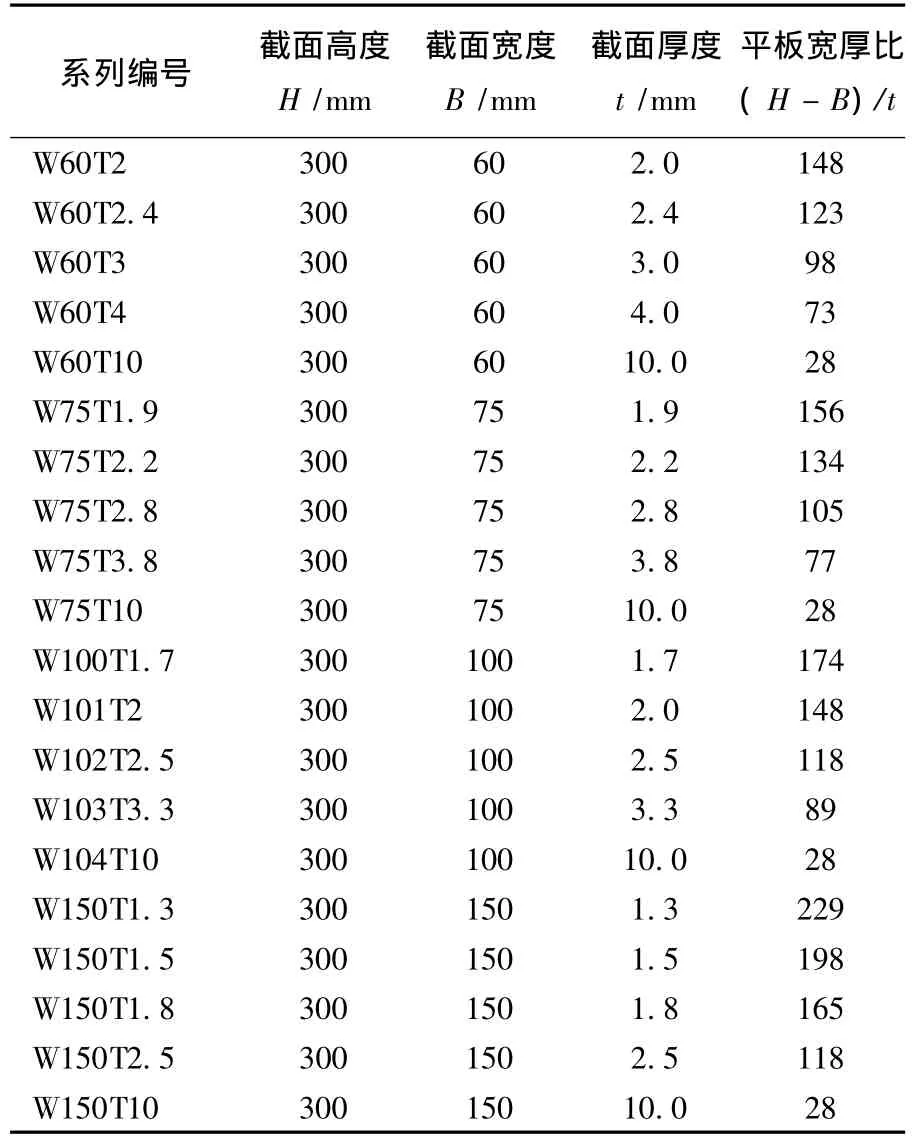
表3 参数分析系列的截面尺寸

4 设计方法

4.1 现行设计规范的计算

我国现行《冷弯薄壁型钢技术规范》基于有效宽度法计算轴压构件承载力.有效宽度法需计算构件每一板件的有效宽度.然而，对于本文所讨论的空心类椭圆截面，有效宽度法无法考虑半圆板件的有效宽度，以及半圆板件的宽度对相邻板件板阻约束系数的影响.由于在试验中未发现半圆板件发生局部屈曲，并且半圆板件抗局部屈曲能力强于平板板件，现做假定如下:

(1)半圆板件均为全截面有效.

(2)计算平板板件的板阻约束系数时，取半圆板件直径为其宽度.

据此，平板板件由两个半圆板件支撑，属均匀受压的加劲板件，故其稳定系数为4;板阻约束系数根据《冷弯薄壁型钢技术规范》5.6.3节计算.

基于以上假定计算试验构件及参数分析构件的轴压设计承载力PCN，并与试验结果Pexp和参数分析结果PFEA进行了比较，同时通过可靠度分析得到了相应的可靠度指标β，详见表4.可靠度分析方法详见北美冷弯薄壁钢结构规范［11］，若β＜2.5即视为不可靠.计算结果表明:Pexp与PCN比值的均值为0.91，变异系数为0.143，可靠度指标为1.46;对于截面长宽比、板件宽厚比等截面尺寸相对较小的构件，《冷弯薄壁型钢技术规范》中的有效宽度法是偏于保守的;对于截面长宽比、板件宽厚比等截面尺寸相对较大的构件，此设计方法是偏于危险的.

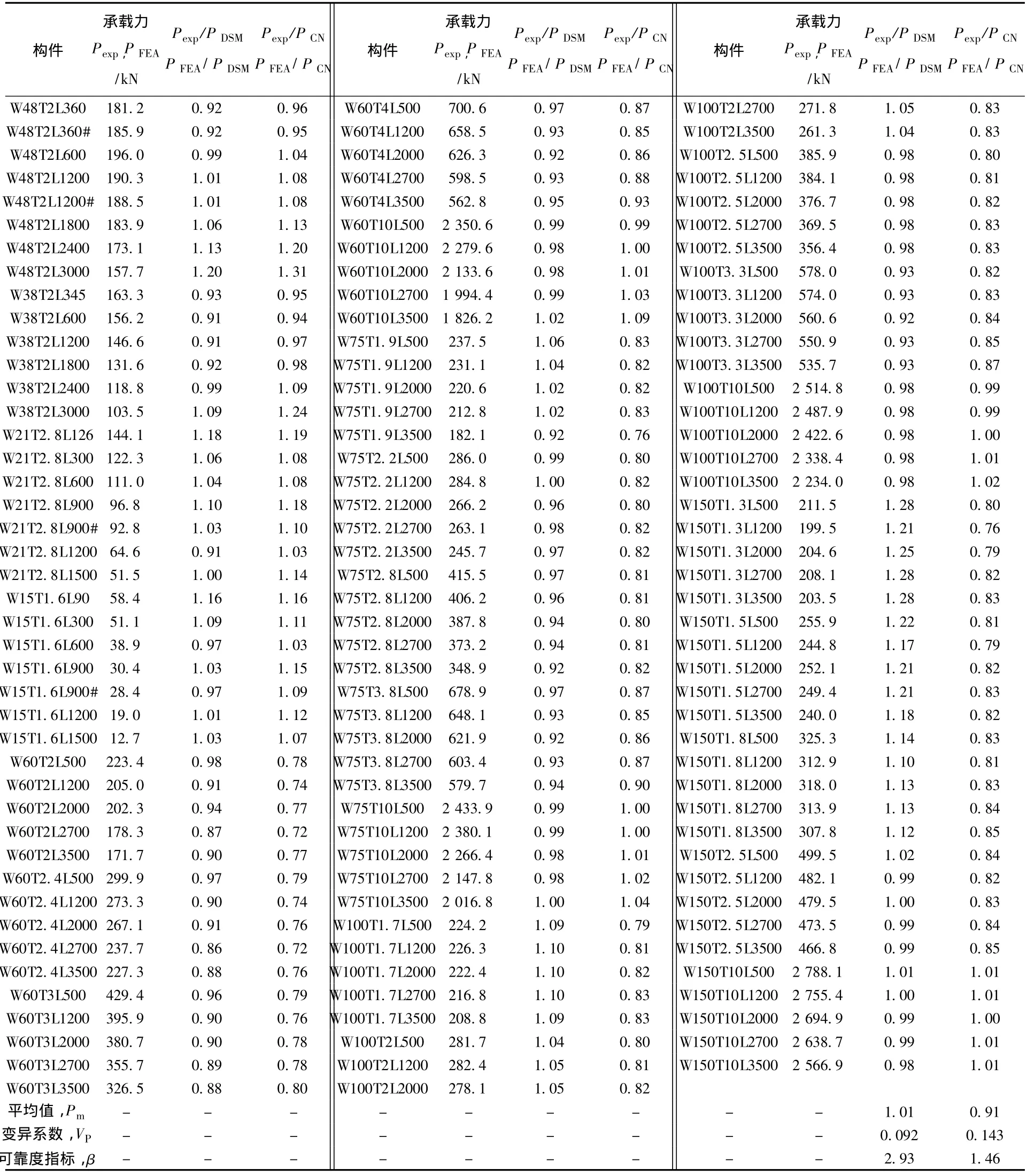
表4 试验及参数分析构件承载力与设计值的比较

4.2 直接强度法的计算

直接强度法现已被北美冷弯薄壁钢结构规范［11］采用，作为构件设计的可选方法.计算公式如下:

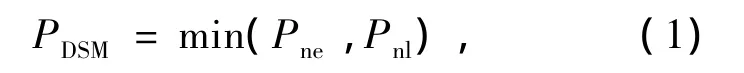
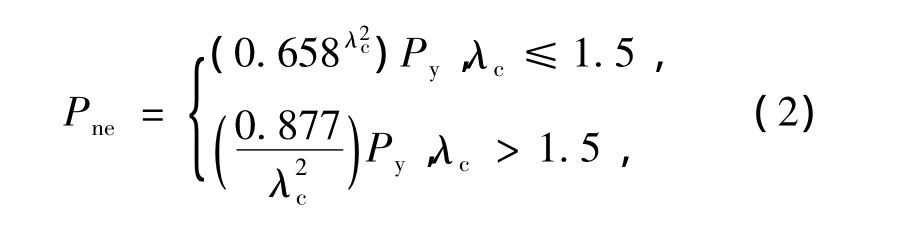
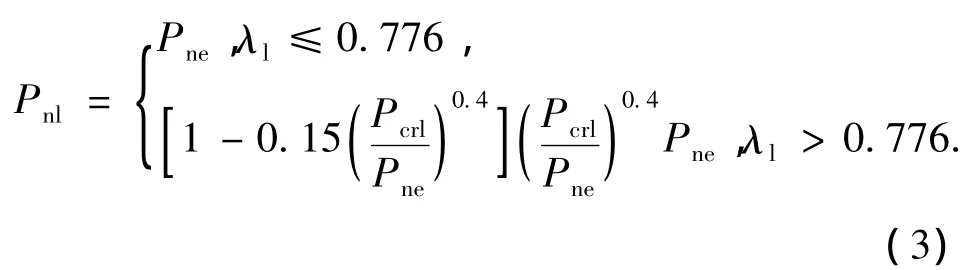
式中:λc=(Py/Poc)0.5，λl=(Pne/Poc)0.5，Py=Afy，Poc=Afoc，Pcrl=Afcrl，foc= π2E/(le/r)2，fcrl为构件弹性局部屈曲应力，A为构件截面积，E为弹性模量，le为构件有效长度，r为截面回转半径.

采用直接强度法计算试验构件和参数分析构件的轴压承载力PDSM及可靠度指标，并与试验结果Pexp和参数分析结果PFEA进行了比较，详见表4，其中 fcrl采用 Abaqus进行计算.图4给出了W100T2.5系列构件采用有效宽度法和直接强度法计算设计承载力的比较.图5为直接强度法设计曲线和数据点的比较.

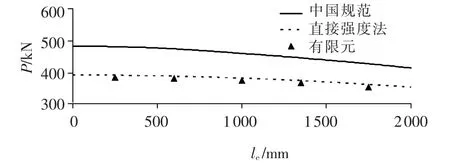
图4 W100T2.5系列构件的有限元与设计承载力比较

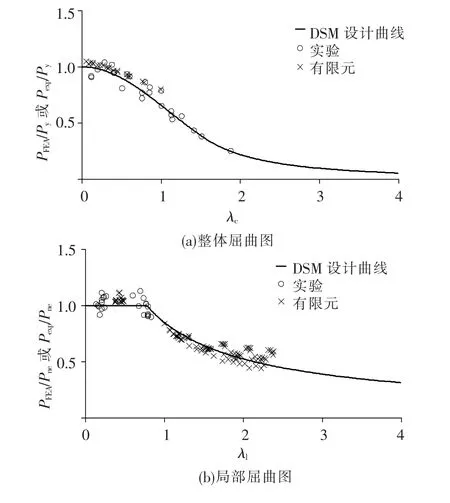
图5 直接强度法设计曲线与有限元和试验数据点的比较

计算结果表明:Pexp与PDSM比值的均值为1.01，变异系数为 0.092，可靠度指标为2.93.可见直接强度法的计算结果与试验和有限元分析结果比较吻合，可靠度指标也较高.与有效宽度法相比，直接强度法不必考虑构件板件有效宽度的计算，计算简单方便，并且计算结果较精确.因此，直接强度法适用于冷弯薄壁钢空心类椭圆截面轴压构件承载力的设计.

5 结论

1)采用Abaqus有限元软件建立了较准确的冷弯薄壁钢空心类椭圆截面轴压构件的数值模型.

2)当前《冷弯薄壁型钢技术规范》中的有效宽度法不能准确地计算冷弯薄壁钢空心类椭圆截面轴心受压构件承载力.

3)北美钢结构设计规范提出的直接强度法可以较准确地计算冷弯薄壁钢空心类椭圆截面轴压构件承载力，其计算结果与试验结果和有限元模拟结果比较吻合，可靠度指标较高，适用于冷弯薄壁钢空心类椭圆截面轴压构件承载力的设计.

［1］中华人民共和国建设部.GB 50018-2002冷弯薄壁型钢技术规范［S］.北京:中国计划出版社，2002.

［2］RUIZ-TERAN A M，GARDNER L.Elastic buckling of elliptical tubes［J］.Thin-Walled Structures，2008，45(16):4427-4447.

［3］CHAN T M，GARDNER L.Compressive resistance of hot-rolled elliptical hollow sections［J］.Engineering Structures，2008，30:522-532.

［4］SCHAFER B W.Local，distortional，and euler buckling of thin-walled columns［J］.Journal of Structural Engineering— ASCE，2002，128(3):289-299.

［5］ZHU J H，YOUNG B.Numerical investigation and design of aluminum alloy circular hollow section columns［J］.Thin-Walled Structures，2008，46(3):1437-1449.

［6］ZHU J H，YOUNG B.Design of aluminum flexural members using direct strength method［J］.Journal of Structural Engineering — ASCE，2009，135(5):558-566.

［7］朱继华，王平.铝合金槽型与加劲槽型截面轴心受压构件数值模拟及设计方法研究［J］.建筑结构学报(增刊)，2010(31):163-168.

［8］LEUNG C F.Structural performance of steel oval sections［D］.Hong Kong:The University of Hong Kong，2007.

［9］SYSTEMÈS D.Abaqus analysis user’s manual，Version 6.8 ［M］. Providence，RI，USA:Dassault Systèmes，2008:156-159.

［10］ZHU J H，YOUNG B.Behaviour and design of aluminum alloy structural members［J］.Advanced Steel Construction，2008，4(2):158-172.

［11］North American Specification(NAS).North American specification for the design of cold-formed steel members［S］.Washington D.C.:American Iron and Steel Institute，2007.

Numerical simulation and design of cold-formed steel oval hollow section compression members

ZHU Ji-hua1，XIN Pei-long2，3，XU Ying3

(1.School of Civil Engineering，Shenzhen University，518060 Shenzhen，Guangdong，China，zhujh@szu.edn.cn;2.Shenzhen Cube Architect Design Company，518055 Shenzhen，Guangdong，China;3.Department of Urban and Civil Engineering，Harbin Institute of Technology Shenzhen Graduate School，518055 Shenzhen，Guangdong，China)

A research was performed on the numerical simulation and design of cold-formed steel oval hollow section compression members to investigate the applicability of existing design specification to the new section.A non-linear finite element model was developed using Abaqus.The numerical results were compared with the test results and it is shown that the numerical model accurately predicted the structural behavior of the compression members.Parametric study was performed using the verified model including 100 members with different cross-section dimensions and lengths.The test and numerical strengths were compared with the design strengths calculated using the current Chinese Code and direct strength method，which is included by the North American Specification for cold-formed steel structures.It is shown that the direct strength method can be used for the design of cold-formed steel oval hollow section members under axial compression.

cold-formed steel;axial compression members;finite element modeling;direct strength method

TU391

A

0367-6234(2011)10-0124-05

2010-04-15.

国家自然科学基金资助项目(50808126，51078237).

朱继华(1976—)，男，博士，副教授.

(编辑 刘 彤)