碎石料干湿循环变形试验及计算方法

曹光栩，宋二祥，徐 明

(1.清华大学 土木工程系，100084 北京，cgx06@mails.tsinghua.edu.cn;2.清华大学结构工程与振动教育部重点实验室，100084 北京)

碎石料干湿循环变形试验及计算方法

曹光栩1，2，宋二祥1，2，徐 明1，2

(1.清华大学 土木工程系，100084 北京，cgx06@mails.tsinghua.edu.cn;2.清华大学结构工程与振动教育部重点实验室，100084 北京)

为深入研究山区机场高填方中常用碎石料的流变及干湿循环变形特性，利用特制的大型侧限固结仪对其进行室内试验.结果表明:同等应力水平下碎石料在干湿循环作用下的变形比常规流变变形的后期增长趋势更为明显，其特点是在每次干湿循环中只是浸水初期变形增长较快，待排干水后变形趋于平缓;经分析干湿循环变形值与循环次数的对数之间有较明显的线性关系.另外，根据试验成果提出了考虑当地降雨情况的常规流变变形和干湿循环变形的简化耦合计算方法，并结合当地降雨规律对云南X机场填方体进行了工后沉降变形计算.

高填方;碎石料;流变变形;干湿循环

近些年随着我国西部大开发战略的实施，西部地区航空运输业得到了快速发展，山区机场高填方地基日益增多，碎石粗粒料以其较好的压缩力学性能成为山区机场高填方工程中主要的填筑材料.据以往工程实测资料，粗粒料填方体在工后几年甚至十几年内还在缓慢地发生沉降变形［1］，这种变形可归结为两个方面:一是粗粒料在荷载作用下的常规流变变形;二是由于日晒雨淋、温度升降等外界环境因素所引起的附加变形.A.K.Parkin［2］较早地在压缩仪上对碎石料进行了流变试验，并利用所得试验结果推测几座已建成的堆石坝的流变变形;沈珠江等［3］在用应力式三轴仪研究了西北口面板坝堆石料流变特性后选用双曲线模型来拟合流变曲线;程展林［4］等利用大型三轴仪针对水布垭大坝的堆石料进行了流变研究，并提出了9参数的堆石料流变模型.对于由众多环境因素所引起的附加变形研究方面，已有学者指出多次降雨或地下水位反复升降所引起的干湿循环变形是其中影响较大的一个因素［5］.Sowers［6］曾对干燥和被水浸湿的砂岩粗粒料分别进行流变试验，并在过程中注水，对比发现干燥的砂岩料变形突然增大而被浸润过的砂岩料变形则没有明显增加;Nobari和Duncan［7］比较早地用常规三轴仪对风干砂试样进行了湿化试验，认为可用试验得出的干、湿两种应力应变曲线来求湿化变形;Lawton等［8］则通过测定不同密度和含水量的试样在不同压力下发生的湿陷沉降大小，得到了不同压力下湿陷沉降的等值线图;Anthiniac［9］通过室内试验和机理分析认为，湿化变形的影响因素包括内因和外因，内因主要有岩石的破碎强度、颗粒形状、矿物成份、密度、级配、含水量及内摩擦角等，外因主要有应力状态、应力路径、浸水时间等;李广信［10］利用大型三轴仪对不同矿物成分、不同密度、不同相似比例的粗料试样进行了湿化试验，并从塑性力学的角度，把湿化过程近似看作加载后又卸载的过程，湿化变形则作为粗粒料由干变湿产生的塑性应变增量，并认为其应变方向正交于清华模型屈服面;殷宗泽［5］则通过大型三轴仪同时研究了粗粒料的流变变形和干湿循环变形，认为两种变形都可以用双曲线来拟合，并把两种变形叠加后的总变形作为正交于椭圆-抛物线双屈服面模型的塑性变形进行计算.因此，目前普遍做法是采用室内大型试验研究流变和湿化变形，而后得出本构关系.

总体来看，目前碎石料的湿化变形研究多是针对堆石坝初次蓄水时的变形.虽然少数研究开始通过大型三轴仪调查堆石坝在干湿循环作用下的长期变形［5，11］，但专门针对山区机场高填方碎石料在干湿循环作用下变形特性的试验研究还未见报道，本文拟通过室内大型试验研究在干湿循环作用下机场高填方碎石料长期变形的发生发展规律，并提出简化算法.

1 试验

1.1 主要试验设备

目前针对堆石坝的研究多采用大型三轴试验，这主要是因为堆石坝的填筑过程近似于等主应力比的加载过程，用三轴仪进行模拟比较合适.值得指出的是，由于细微的薄膜漏水［13］、粗粒料试验中的薄膜贯入效应［14］导致在大型三轴试验中体变量测不准等问题一直未得到较好地解决，这对长期流变和干湿循环试验的试验结果都可能造成很大的误差.而本文所研究的山区机场高填方工程填筑面积很大，其填料的应力路径与一维侧限压缩状态比较接近，采用侧限压缩试验来研究填料的力学特性更为合适.刘宏等［14-15］曾选用侧限固结仪对九黄机场和贵州龙洞堡机场工程的填料进行过流变试验研究.因此，此次流变和干湿循环变形试验选用大型侧限固结仪来进行.

考虑到需要长期稳定的施加荷载，该固结仪在设计上采用杠杆加压方式对试样进行侧限压缩，并且在试验过程中可通过调平衡装置保持杠杆水平，从而实现压力始终在竖直方向.另外利用外部的有机玻璃管还可对内部试样进行浸水饱和.该固结仪可提供最大竖向压力1.34 MPa，试样直径200 mm，高200 mm.

1.2 试样制备

山区机场填方中所用碎石料一般为现场常规爆破产生，粒径较大，所以，试样需要根据现场填料的级配进行缩尺制备，本文采用的缩尺方法为混合缩尺法［16］:先用相似级配法将X机场现场填料级配缩尺到原来的1/2，再用等量替代法把最大粒径缩尺到40 mm(图1所示).试样与现场填料岩性相同，均为西部山区常见的石灰岩碎石料，经过自然风干.具体制备时每个试样分为4层填筑，每层高度约5 cm;试样密度参照现场标准控制在2.0 g/cm3左右.

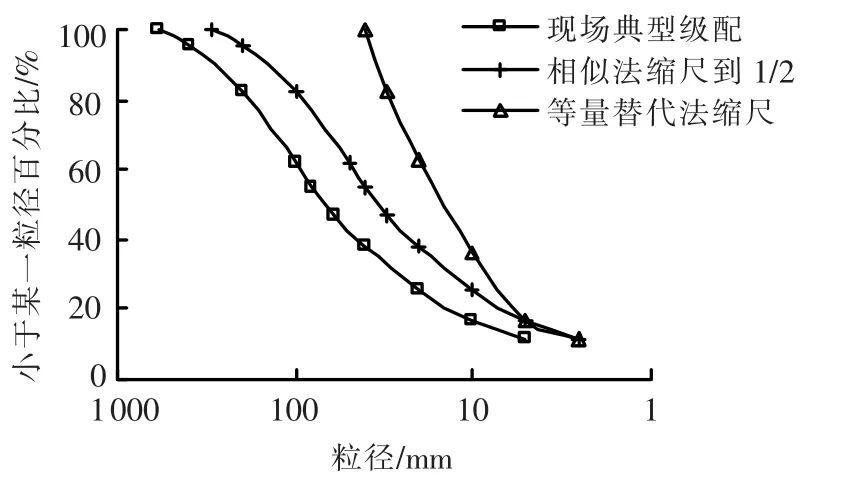
图1 缩尺前后灰岩碎石的级配曲线

1.3 试验方案

本次试验共分为两种:第一种是仅在荷载作用的下普通流变试验;第二种是荷载和干湿循环共同作用下的变形试验.从第二种试验的试验值中扣除相应荷载下的普通流变变形值即得到需要研究的干湿循环变形值.其中干湿循环变形试验采取在某一荷载下从试样底部浸水湿化，等变形稳定后再将水排干的方法近似模拟实际的一次晴雨过程.当然由于试验条件限制若等到试样完全干燥再进行下一次浸水湿化是很困难的，因此，需要选择较为合理的排水放置时间.王海俊等［17］曾用大型三轴仪针对花岗岩碎石料做过类似试验，试样直径101 mm，高200 mm，经过分析不同排水条件的试验结果后认为在自由排干0.5 h后试样内部进水已基本排干，并把0.5 h作为干湿循环试验中排水放置时间.本试验选择1 h作为排水放置时间.

此次 试 验 竖 向 荷 载 在 0.14、0.34、0.54、0.74、0.94 和 1.14 MPa 等 6 个级别进行分级加载.因为本试验以X机场工程为模拟背景，其最大填方高度约50 m，填筑体底层填料的最大竖向应力在1 MPa左右，试验中为了考虑此情况加载的最大荷载级别才设定为1.14 MPa.

1.4 试验具体过程

试验的基本操作步骤、数据记录间隔时间以及稳定标准均参照文献［16］.

具体过程如下:

1)碎石料共分4层夯实填入到固结仪内，每层高度5 cm左右.夯实完毕后首先测量起始高度，并在试样上部覆盖滤纸、透水板，然后放下加压盖，密合传压活塞及横梁并用1.0 kg的压力进行预压，再装好百分表，记下初始读数.

2)在加第1级荷载的同时立即开动秒表，按照要求读数，分级加载时稳定标准［17］为最后连续1 h的应变值不超过5×10-4.

3)变形稳定后再加下一级荷载.本试验共分为6 级加载.分别选择其中 0.34、0.74、0.94 和1.14 MPa 4个荷载级别进行较长时间的普通流变变形试验.

4)完成普通流变试验后，重新装好试样，待加载到0.34 MPa变形稳定后对试样进行浸水饱和，维持水头与试样同高，浸水时间持续1 h，然后将水迅速排干放置1 h;再按同样的时间间隔对试样反复浸水湿化，共进行6次干湿循环操作，持续约12 h.全部完成后依次更换3个新试样按照同样的方法分别在0.74、0.94、1.14 MPa 下进行干湿循环变形试验.

2 结果及分析

2.1 普通流变试验规律

试验中只在0.34、0.74、0.94 和 1.14 MPa 荷载下维持流变变形 6 ～7 d，而 0.14、0.54 MPa荷载下持续时间较短，一般1～2 h.绘制出各级荷载下压缩变形S和时间对数logt的关系曲线，取曲线的反弯点前后两段曲线切线的交点作为瞬时弹塑性变形和流变变形的分界点［18］.各级荷载下的流变变形如图2所示.

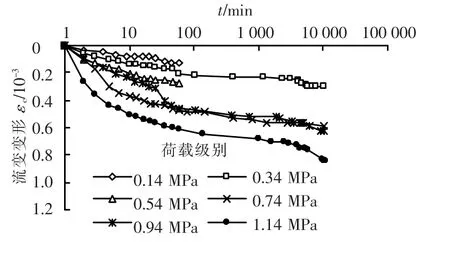
图2 碎石料流变变形－时间对数曲线

从图2可以看出，碎石料的初始流变速率和流变变形值基本上随着应力水平的增加而逐渐增大.在较短时间和较低应力水平下流变变形与时间对数可以近似用线性关系来描述，但随着时间的延长以及压力水平的提高流变与时间对数不再具有较好的线性关系.

2.2 干湿循环试验变形规律

图3为1.14 MPa应力水平下普通流变试验与干湿循环变形试验的变形曲线对比，由于考虑到碎石填料在实际填筑过程中很可能已经经历过强降雨过程，即竣工后若再次遭遇强降雨然后风干已经不属于初次干湿循环，把干湿循环变形曲线的初次干湿循环变形值扣除，不计入干湿循环长期变形［5］.从图 3 可以看出，1.14 MPa应力水平下碎石料在有限的几次干湿循环作用下的变形与同等应力水平下的普通流变变形相比后期的增长趋势依然很明显，尚未达到稳定，因此，干湿循环作为一种影响碎石料长期变形的重要因素是不能忽视的，尤其对于高填方工程.

图3 1.14 MPa荷载下干湿循环变形与普通流变曲线对比

用图3中干湿循环变形值减去普通流变变形试验值，所得结果即可以近似认为是1.14 MPa应力水平下仅由干湿循环所引起的变形，同样方法也可以得到其他应力水平下仅由干湿循环作用所引起的变形，如图4所示.可以看出，一方面干湿循环变形的大小随应力水平的提高是逐渐增大的;另一方面，碎石料在后面几次循环中每次浸水初期变形有相对较大的增长，而后变形快速趋于稳定，整体上呈现出类似于台阶状的变化，并且应力水平越高这种规律越显著.

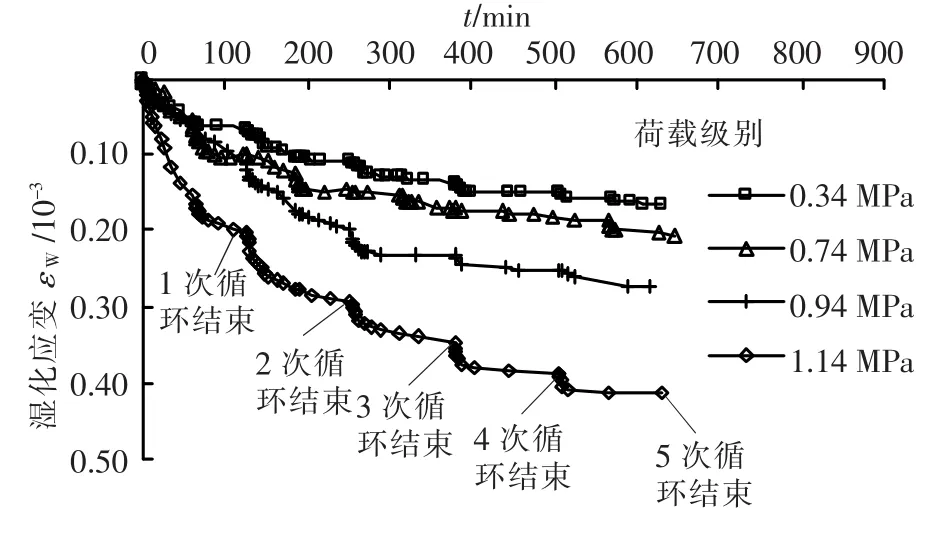
图4 碎石料干湿循环变形曲线

2.3 机理分析

碎石料常规流变变形产生的原因主要是在经历了加载初期较大的弹塑性变形之后碎石颗粒仍会继续在较小范围内出现错动滑移，这样就引起颗粒之间应力的重分布，导致碎石颗粒棱角的少量破碎，颗粒排列得以继续调整［19］.与之相比碎石填料在长期晴雨反复作用下产生干湿循环变形的原因相对要复杂一些，从总体上分析主要来自于以下几个方面:

1)由于雨水或地下水的反复浸润导致颗粒强度的降低，在较大荷载作用下发生碎石颗粒的破碎细化，引起颗粒排列的重新调整;

2)因为水分的润滑作用导致颗粒接触部位的摩擦系数降低，从而使原来处于摩擦平衡状态的颗粒之间发生进一步的错动滑移;

3)当出现碎石颗粒破碎时，雨水的反复浸润为新鲜破碎面的继续湿化提供了可能，碎石颗粒会在新断面出现滑移或使新棱角发生进一步的破碎;

4)当碎石颗粒被浸润时，其质量会有所增加，在这种新增加的荷载作用下会产生一部分不可恢复的塑性变形;

5)地下水在碎石颗粒之间渗流速率较大，很小一部分细颗粒会被水流搬运，位置发生迁移，从而引起碎石填料的局部级配发生变化，在其他扰动下该部位较粗颗粒的位置也会重新调整;

6)如果碎石料的母岩是易受水侵蚀的岩石，如碳酸盐类岩石碎石料，当受到含有CO2的地下水长期浸润冲刷时会发生化学风化，从而引起其强度降低，导致更大的破碎变形.

以上几个方面引起的变形大小是有差别的，一般来说1)、2)和3)所引起的变形占总体干湿循环变形的主要部分.另外，以上各影响因素之间并不是孤立的，他们之间会相互影响相互促进，如颗粒破碎可能产生更多的细小颗粒，而这些小颗粒有可能进一步受渗流作用位置发生迁移.由于室内试验条件有限，且持续时间相对较短，仅近似模拟了1)、2)、3)等几种因素引起的干湿循环变形.

对比常规流变变形和干湿循环变形发生的机理，可以看出两种变形都主要来自于颗粒的破碎和滑移，发展的最终效果都会使碎石料越来越密实，可以说某一总的变形值(无论来自于哪种变形)对应着碎石料的某一密实状态.当碎石料密实到一定程度这两种变形必然都会停止或达到可以忽略的程度.因此，干湿循环变形的发生必然会使后面蠕变变形可发展的空间减小，同样蠕变变形的不断发展也必将影响再次发生的干湿循环变形的大小，两种变形应该是相互耦合的.

2.4 常规流变变形和干湿循环变形的计算方法

首先，对于常规流变变形经分析对比发现采用双曲线模型来近似模拟较为合适:

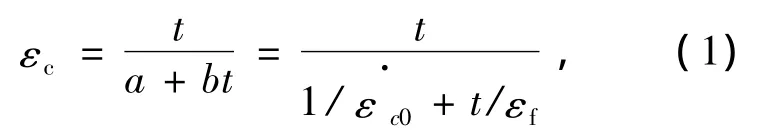
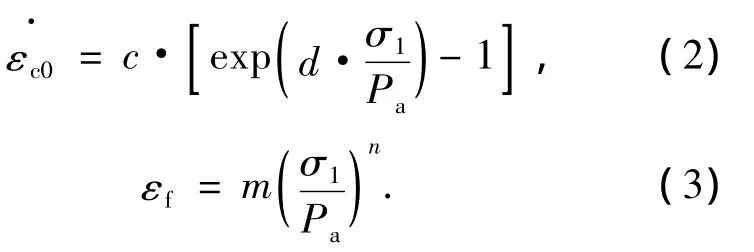
其中Pa为标准大气压值(Pa=1.01×105Pa)，量纲与竖向应力 σ1相同;c，d，m，n为4个试验常数.对于本试验中石灰岩碎石料，采用X机场典型级配进行缩尺制备，夯实后密度为ρ=2.02 g/cm3，4 个试验常数分别为c=0.537 4，d=0.025 55，m=0.110 0，n=0.855 7.

其次，通过2.3中分析可知引起干湿循环变形的因素较多，并且各种因素之间会相互影响，目前从理论上比较明确地计算各种因素引起的干湿循环变形还较为困难，所以，仍选用比较常用的数学函数模型从宏观上描述干湿循环变形.图4中显示碎石料的干湿循环变形与干湿循环次数n关系较明显，因此，可以将循环次数n作为变量来刻画碎石料在干湿循环作用下的变形，如图5所示.本文选用对数模型来近似计算图5中单独由干湿循环作用所引起的碎石料的变形:

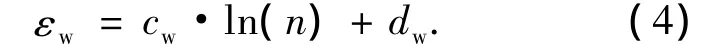
其中cw和dw为试验拟合参数，不同应力水平下的拟合参数见表1.

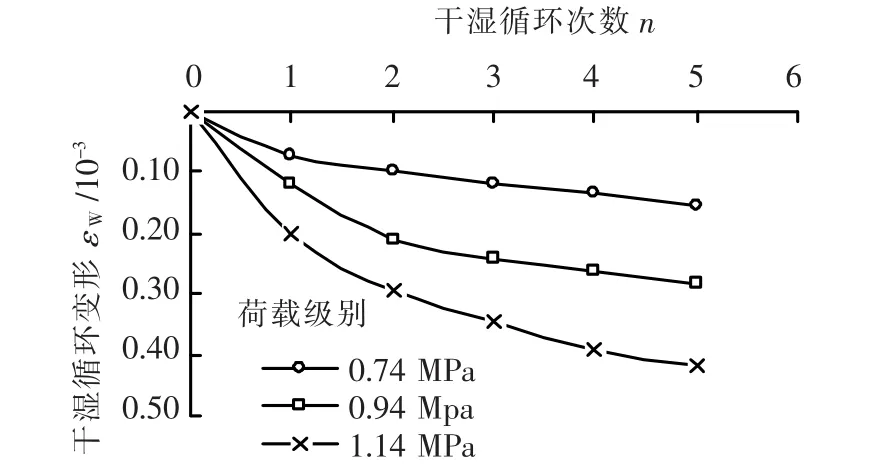
图5 不同荷载下碎石料干湿循环变形－循环次数n曲线

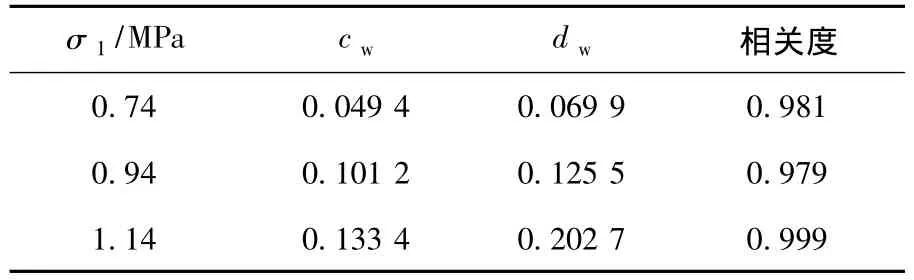
表1 对数曲线拟合参数

根据表1数据还可以进一步拟合cw和dw两参数与应力水平的关系，经比较cw与应力水平之间也呈现出对数函数关系;dw与应力水平则可用幂函数关系来描述:

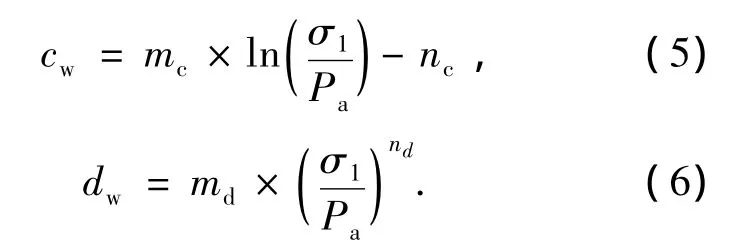
式中:σ1为竖向应力;mc、nc、md和nd为拟合参数，对于本试验所用灰岩碎石料，按照X机场填料缩尺制备，平均密度 ρ=2.02 g/cm3，mc、nc、md和 nd分别为 0.195 3、0.333 6、0.54 × 10-3和2.449.利用上述计算公式和拟合参数可计算碎石料不同应力水平下进行n次干湿循环所产生的变形值，计算值与试验值对比如图6所示.

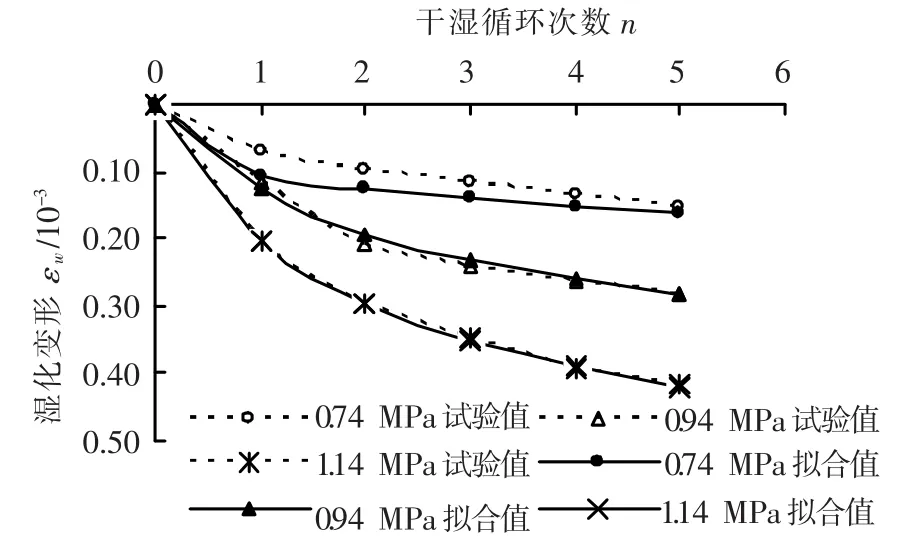
图6 拟合不同荷载下碎石料干湿循环变形－循环次数n曲线

室内试验对试样进行的1次干湿循环近似和实际现场条件下碎石料经历1次强降雨过程相对应，因此，现场条件下碎石填料经历的强降雨次数可以认为是其所经历的干湿循环次数.进行干湿循环变形计算时可以统计所在场区长期强降雨分布规律，然后用较为合适的函数将强降雨次数n与时间t联系起来，这样就可以用实际时间来计算碎石填料的干湿循环变形.

表2为X机场场区强降雨统计规律，为了方便计算直接拟合累计强降雨次数∑n与对应时间t(近似认为到月底时前面降雨全部完成)的关系，图7采用了式(7)所示的分段线性函数来计算该机场场区一年中累计降雨次数∑n与时间t的关系.计算时间超过1年后，可以将下一年1月1日作为起点按此函数重复计算，并注意累加上一年计算出的降雨次数.得到某一时间段内的强降雨次数即可以按照式(4)～(6)来计算干湿循环变形.

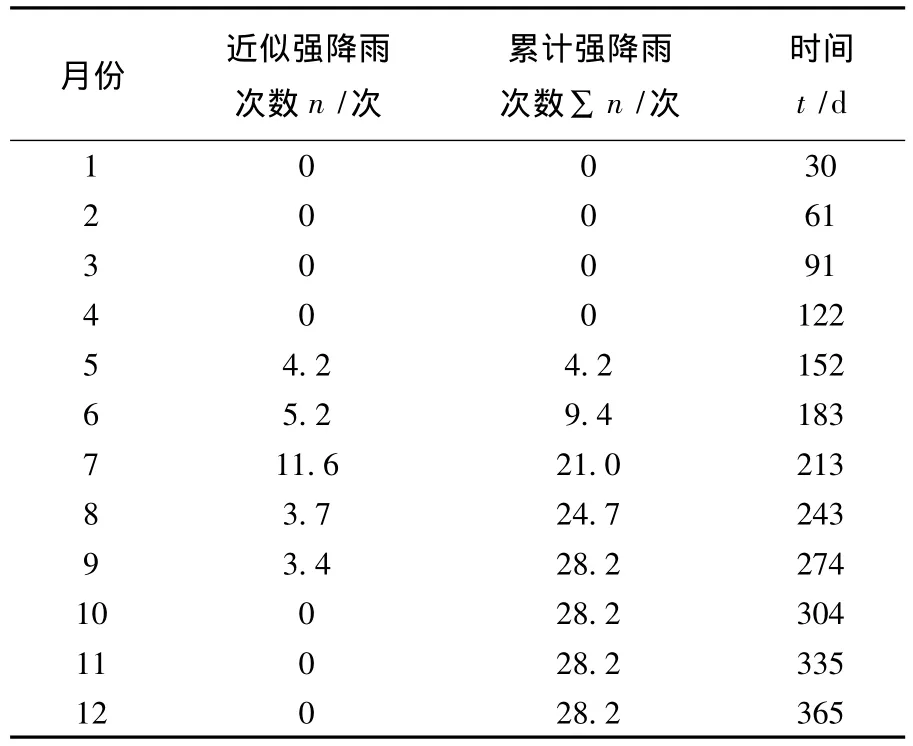
表2 云南X机场场区年平均强降雨统计规律

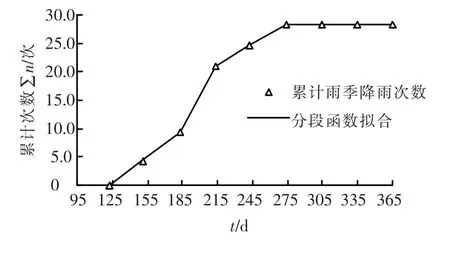
图7 一年中降雨累计次数∑n－时间t关系曲线

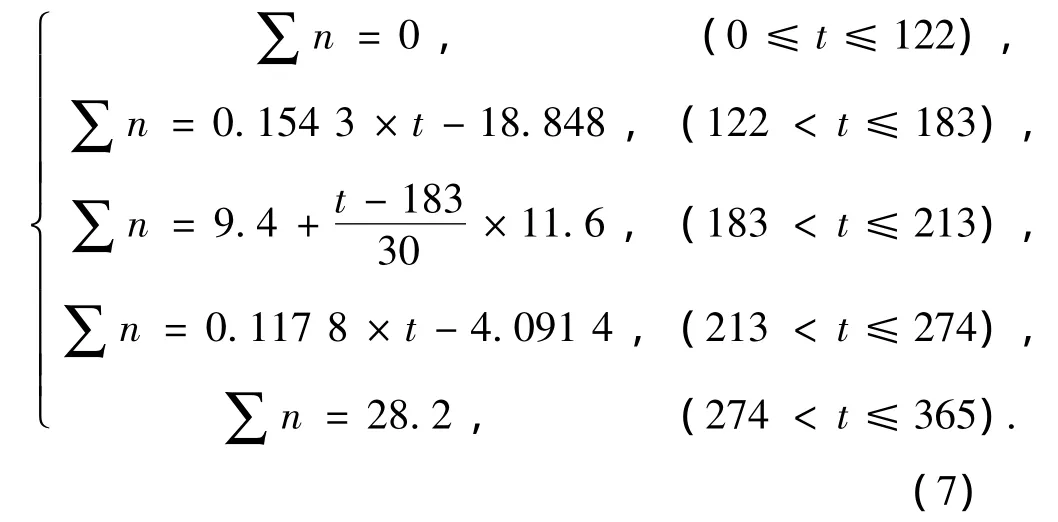
式(1)～(3)和式(4)～(6)分别是针对碎石料常规流变变形和干湿循环变形的单独计算方法，而实际中两种变形是耦合在一起的.所以，下面介绍一种能同时考虑两种变形的简化耦合计算方法:

1)对于给定的某一应力状态(荷载)下的一薄层土单元，当尚未发生干湿循环变形时，土单元的变形随时间按一确定的双曲线规律发展，如图8曲线a中由点O到点A所示;曲线b则对应单独的干湿循环变形，其起始时刻O'与土单元第一次发生干湿循环变形时刻相对应;

2)当到达点A时发生干湿循环变形，则令干湿循环变形初值εw1等于现在已经发生的变形值εc1，利用式(4)计算干湿循环初始次数n1;

图8 流变变形和干湿循环变形耦合计算示意图

3)设定一较短的时间间隔Δt，通过实际降雨曲线式(7)计算tA到时间tA+Δt内发生的干湿循环次数Δn1，而后通过式(4)计算由n1到n1+Δn1期间干湿循环所增加的变形量Δεw1;

4)再将(εc1+Δεw1)作为此时的总变形，找到曲线a上与之对应的一点D，此后的流变变形就是从D点开始按曲线a向后发展，根据式(1)计算时间Δt内的流变值Δεc1;

5)在总的时间轴中只计入一次Δt，但在tA+Δt内发生的总变形计为(εc1+Δεw1+Δεc1)，因为干湿循环变形和流变变形是同时发生的，而从前面试验结果可以看出湿化变形发展得更为迅速，所以，上面方法令湿化变形先发生来影响同一时间内的流变变形来近似模拟两种变形的耦合效应;

6)若以后还有干湿循环发生即按上面2)～5)步骤重复进行;如果到第i次进行计算时总变形εc1+∑(Δεw(t)+Δεc(t))的值等于或超过了流变变形双曲线的渐进值εf，则认为流变变形不再发生，而只是发生干湿循环变形.

对于大面积水平成层的高填方工程，可以参照普通沉降计算中的分层总和法，将实际填方体分为若干层，每层中心部位的应力代表该层的应力水平，利用上面方法计算每层填土自压力稳定后经历时间t的变形值Si，那么全部填方体经历时间t后的总变形值S(mm)等于各层变形值之和，即

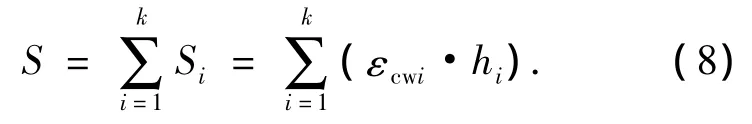
式中:k为计算深度范围内的分层数;hi为第i层土厚度，m;εcwi为第i层土单元流变与干湿循环变形的耦合计算值，10-3.

3 实例计算

按照上述流变和干湿循环变形的耦合计算思路编制了高填方工后沉降变形计算程序，并对云南X机场某标段道槽区填方体进行了工后沉降计算.该标段道槽区所用填料基本为碎石料，所选计算点填方高度约40 m，计算时根据实际碾压厚度每1 m分为一层，计算结果如图9所示.可以看出，在没有降雨的影响下道槽区工后沉降变形在最初的5～6个月内发展较快，而后变形速率逐渐减缓;之后当进入工后第一个雨季时由于降雨的影响，变形速率明显增大，雨季过后沉降速率又恢复到较低水平;在经历两个雨季后流变和降雨引起的干湿循环变形基本都趋于稳定.由此也可以看出，干湿循环变形对山区机场高填方工后沉降的影响是较明显的，而要十分准确地预测机场填方地基工后放置多长时间可以施作跑道道面则必须较为细致地考虑当地降雨规律.

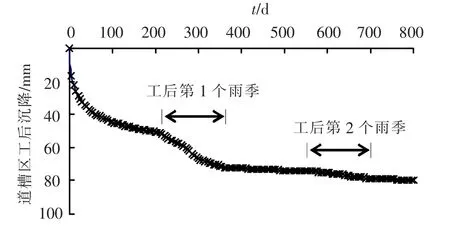
图9 云南X机场某标段道槽区工后沉降计算结果

X机场设计运营期为20年，通过上述程序可以进一步计算该填方位置20年(约7 300 d)后的工后沉降值约为83 mm，而上面经历一个雨季后的沉降值从图9中可看出约61 mm，所以，如果填方体在放置一个雨季后施工跑道道面，剩余沉降量约为22 mm，是可以满足一般山区机场跑道地基工后最终剩余沉降量应控制在40 mm以内的要求.当然如果工期安排允许，放置两个雨季后再铺筑道面对机场跑道的运营安全将更为有利.

4 结论

1)与同应力水平下的流变变形相比干湿循环引起的变形是相当可观的，并且后期增长趋势依然明显.

2)碎石料的干湿循环变形值随循环次数n的增加呈现出台阶状的变化规律.在每次干湿循环中只是浸水初期变形增长明显，而后在较短时间内趋于平缓.

3)同一应力水平下碎石料的每次干湿循环变形的大小随循环次数的增多逐渐减小;不同应力水平下干湿循环变形大小随着应力水平的提高而逐渐增大.

4)如无降雨影响粗粒料填方体流变变形在最初的5～6个月内发展较快，而后变形速率逐渐减缓.

5)雨季中多次晴雨反复所引起的干湿循环变形导致填方体沉降速率明显增大，但在经历两个雨季后干湿循环变形基本也趋于稳定.因此，山区机场高填方工程竣工后放置1～2个雨季再进行跑道道面施工对其后期的安全运营是十分有利的.

从上述试验和计算结果可以看出，干湿循环变形对填方体的长期沉降变形影响较大，直接关系到高填方机场工后何时可以施工跑道道面，所以必须给与足够重视，而实际上在以碎石料或土石混合料为主要填料的此类山区高填方工程中并没有认真全面地考虑干湿循环作用对长期变形的影响.因此，开展碎石料以及土石混合料的循环湿化变形研究具有较大的理论意义和实用价值.最后需要说明的是，各种研究手段均有优点和不足之处，而室内试验也不可能全面反映工程现场中影响填料变形的各种因素，如能再结合现场实测分析确定模型参数，则能取得更好的结果.

［1］徐明，宋二祥.高填方长期工后沉降研究的综述［J］.清华大学学报:自然科学版，2009，49(6):786-789.

［2］NEVES E M.Advance s in rockfill structure［M］.London:Kluwer Academic Publishers，1991.

［3］沈珠江，左元明.堆石料的流变特性试验研究［C］//沈珠江土力学论文选集.北京:清华大学出版社，2005:377-381.

［4］程展林，丁红顺.堆石料工程特性试验研究［J］.人民长江，2007，38(7):110-114.

［5］殷宗泽.高土石坝的应力与变形［J］.岩土工程学报，2009，31(1):1-14.

［6］SOWERS G F，WILLIAMS R C，WALLACE T S.Compressibility of broken rock and the settlement of rockfills［C］//Proc 6th Int Conf on Soil Mech and Foundation Eng.Toronto:University of Toronto Press，1965:561-565.

［7］NOBARI E S，DUNCAN J M.Movements in dams due to reservoir filling［C］//Performance of Earth and Earth Supported Structures.California:Dept.of Civil Engineering，University of California，1972:797-816.

［8］LAWTON E C，FRAGASZY R J，HARDCASTLE J H.Collapse of a compacted clayey sand［J］.ASCE J Geotech Eng，1989，115(9):1252-1267.

［9］AHNTINIAC P，BONELI S.Modelling saturation settlements in rockfill dams［C］//Proceedings of the International Symposium on New Trends and Guidelines on Dam Safety.［S.l.］:Barcelona Spain，1998:17-19.

［10］李广信.堆石料的湿化试验和数学模型［J］.岩土工程学报，1990，12(5):58-64.

［11］孙国亮，孙逊，张丙印.堆石料风化试验仪的研制及应用［J］.岩土工程学报，2009，31(9):1462-1466.

［12］SEVI A F，LOUIS G，T ANDY W.A large-scale triaxial apparatus for prototype railroad ballast testing［J］.Geotechnical Testing Journal，2009，32(4):297-304.

［13］CHAVEZ C，ROMERO E，ALONSO E E.A rockfill triaxial cell with suction control［J］.Geotechnical Testing Journal，2009，32(3):219-231.

［14］刘宏，张倬元.四川九寨黄龙机场高填方地基变形与稳定性系统研究［M］.成都:西南交通大学出版社，2006.

［15］韩世莲，周虎鑫，陈荣生.土和碎石混合料的蠕变试验研究［J］.岩土工程学报，1999，21(2):196-199.

［16］中华人民共和国水利部.SL237-1999土工试验规程［S］.北京:中国水利水电出版社，1999.

［17］王海俊，殷宗泽.堆石料长期变形的室内试验研究［J］.水利学报，2007，38(8):914-919.

［18］CHENG C M，YIN J H.An improved method for estimating the time and strain at the end of the＂primary＂consolidation of a clayey soil with non-linear creep［J］.Geotechnical Engineering，2007，38(2):105-109.

［19］COOP M R，SORENSEN K K，FREITAS B T.Particle breakage during shearing of a carbonate sand［J］.Geotechnique，2004，54(3):157-163.

Study on experiment and calculation method of dry-wet cycle characteristics of rockfills

CAO Guang-xu1，2，SONG Er-xiang1，2，XU Ming1，2

(1.Department of Civil Engineering，Tsinghua University，100084 Beijing，China，cgx06@mails.tsinghua.edu.cn;2.Key Laboratory of Structural Engineering and Vibration of Ministry of Education，Tsinghua University，100084 Beijing，China)

With the specially designed large－scale oedometer，routine rheological tests and dry－wet cycle tests have been conducted on specimens to investigate the rheological and dry－wet cycle characteristics of rockfills，which have been widely used in the high － fill foundations of mountain airport.The test results demonstrate that the long term deformation due to dry－wet cycle grows more evidently than the routine rheological deformation，which increases rapidly during early immersion，and gradually flattens after draining the water.There is approximately a logarithmic relationship between dry－wet cycle deformation and cycle numbers.In addition，a simplified coupling calculation method that can meanwhile compute the rheological deformation and dry－wet cycle deformation is proposed，by which the settlement of foundation after construction in X airport of Yunnan Province is computed according to local rainfall law.

high fill;rockfills;rheological deformation;dry－wet cycle

TU411

A

0367－6234(2011)10－0098－07

2010－04－15.

国家高技术研究发展计划项目(2007AA11Z113);教育部博士点新教师基金资助项目(200800031061);国家自然科学基金资助项目(50978140).

曹光栩(1982—)，男，博士研究生;

宋二祥(1957—)，男，教授，博士生导师.

(编辑 刘 彤)