柔性航天器大角度姿态机动的变论域分形控制

杨思亮，徐世杰

(北京航空航天大学 宇航学院，100191 北京，yangsiliang@sa.buaa.edu.cn)

柔性航天器大角度姿态机动的变论域分形控制

杨思亮，徐世杰

(北京航空航天大学 宇航学院，100191 北京，yangsiliang@sa.buaa.edu.cn)

针对具有开环树状拓扑结构的柔性多体航天器，基于真－伪坐标形式的拉格朗日方程，建立柔性多体航天器的动力学模型，充分考虑了柔性航天器的时变与不确定性的动力学特征，设计了改进的变论域分形模糊控制器，并对该系统进行了仿真验证.仿真结果表明，该方案回避了实时计算收缩因子所导致的论域范围实时收缩的缺点，实现了对柔性多体航天器大角度姿态机动的有效控制，同时保证了航天器柔性附件振动的有效抑制.

航天器制导与控制;柔性多体航天器;大角度姿态机动;变论域;分形控制

经过几十年的努力，尽管关于柔性多体航天器的姿态控制研究已取得很大成果［1－2］，但仍停留在需要精确数学模型的基础之上.一方面，发射重量的限制和构型的对称性决定了这类航天器具有刚度低、柔性大、阻尼弱、基频低和模态密级等复杂的动力学特性，而且大型柔性附件的周期性转动和非周期性跟踪与扫描运动使对象又呈现出一种多体和时变的特点;另一方面，建立柔性多体航天器的精确的数学模型还很困难［3］.这对依赖于精确数学模型的经典控制理论和现代控制理论提出了挑战.而模糊控制理论不需要精确数学模型，适应于这一复杂大系统的控制问题.但是，模糊控制的主要缺陷是精度不太高，自适应能力有限，易产生振荡现象.于是，模糊控制器在航天领域的应用范围仍然很有限.

变论域模糊控制系统是一种输入与输出变量论域取值合理变化的模糊控制系统，是改变模糊控制性能的主要方法之一.文献［4］基于 Lyapunov原理提出参数自适应律的概念，得到了自适应模糊控制系统稳定性的一般准则［5－6］，但并没有使用变论域技术，所以控制效果不佳;文献［7］对航天器刚柔耦合非线性系统的自适应变论域模糊控制问题进行了研究，但其中采用的都是进行实时计算的收缩因子，收缩因子的实时计算导致论域范围实时收缩，从而不能对未来的输入信号进行规则约束，其实用性还有待进一步研究.

本文针对上述问题，提出一种柔性多体航天器大角度姿态机动的变论域分形控制方案.首先针对具有开环树状拓扑结构的柔性多体航天器，基于真－伪坐标形式的拉格朗日方程，建立柔性多体航天器动力学模型，充分考虑了柔性航天器的时变与不确定性的动力学特征，设计了改进的变论域分形模糊控制器，并对该模型进行系统仿真实验.仿真结果表明，该方案可回避实时计算收缩因子所导致的论域范围实时收缩的缺点，实现对柔性多体航天器大角度姿态机动的有效控制，同时保证航天器柔性附件振动的有效抑制，具有一定的理论意义和工程应用价值.

1 卫星姿态动力学模型

对于带有大型太阳帆板的挠性航天器，使用有限元方法对挠性太阳帆板进行离散，只考虑前三阶的挠性模态.取姿态角和模态坐标为系统的广义坐标，使用真－伪坐标形式的拉格朗日方程可以得到具有惯量不确定性的航天器动力学方程为

式中:I是航天器的转动惯量矩阵;ΔI是由于太阳帆板转动引起的惯量不确定性增量;C是挠性附件与星体的耦合系数;u是三轴控制力矩;w是干扰力矩;η是挠性模态坐标;K=Λ2;D=2ξΛ，ξ为挠性附件模态阻尼系数矩阵，Λ为挠性附件模态频率矩阵.假设D、K均正定，即挠性结构含有非负的惯性阻尼.

为避免欧拉角带来的大角度奇异问题，采用如下修正罗德里格斯参数(Modified Rodrigues Parameters，MRPs)描述的挠性航天器姿态运动方程［8］:

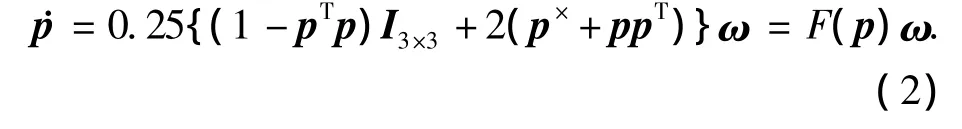
其中:ω =［ω1ω2ω3］T为星体角速度;p=［p1p2p3］T，代表航天器本体相对于惯性空间的MRPs;p×代表向量p的反对称矩阵.

由上面的挠性航天器动力学和姿态运动方程可知，刚体的姿态运动与挠性体的振动互相影响、互为激励.外力矩在促使刚体姿态变动的同时，也引起挠性体变形，另一方面，挠性体的任何变形都引起刚体的角位移变化.此外，还有一些干扰力矩直接影响刚体的姿态运动，如引力梯度力矩、大气阻力力矩、太阳光压力矩、地磁力矩等对卫星姿态的影响都不可忽略.为此，所设计的控制器必须能有效地抑制外界干扰，同时对刚体与挠性体之间的影响应有自适应能力，以保证卫星姿态的控制精度.至此，挠性卫星姿态控制可归结为:根据式(1)～(2)，构造控制律 u，使得当t→ ∞ 时，p→pt，ω →0，η →0，其中 pt代表目标姿态.

2 变论域分形模糊姿态控制器设计

2.1 变论域模糊控制器

变论域的思想最早见于文献［9］，“在规则形成(形状)不变的前提下，论域随着误差变小而收缩(亦可随着误差增大而膨胀)”.变论域模糊控制系统是一种输入与输出变量论域取值合理变化的模糊控制系统，对输入和输出论域的取值进行合理设计，能达到很好的控制效果.

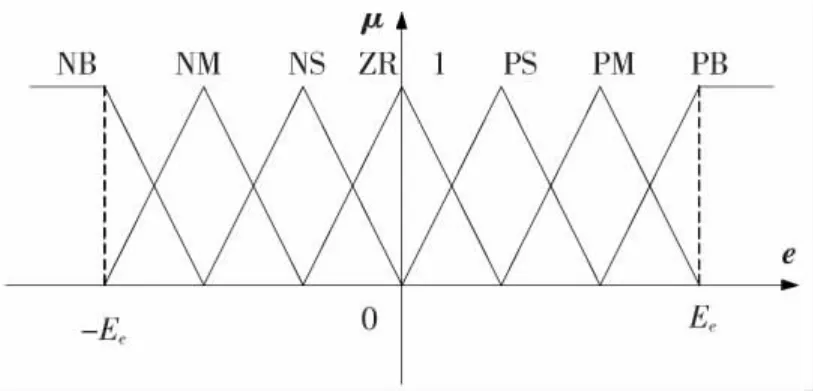
图1 初始论域及其模糊划分

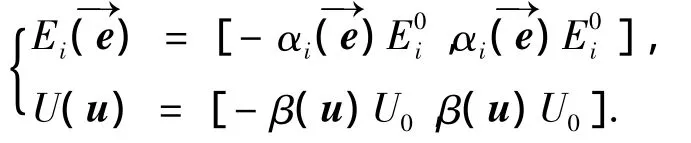
式中αi和β(u)称为论域的伸缩因子.在伸缩因子的作用下，论域的膨胀与压缩如图2所示.

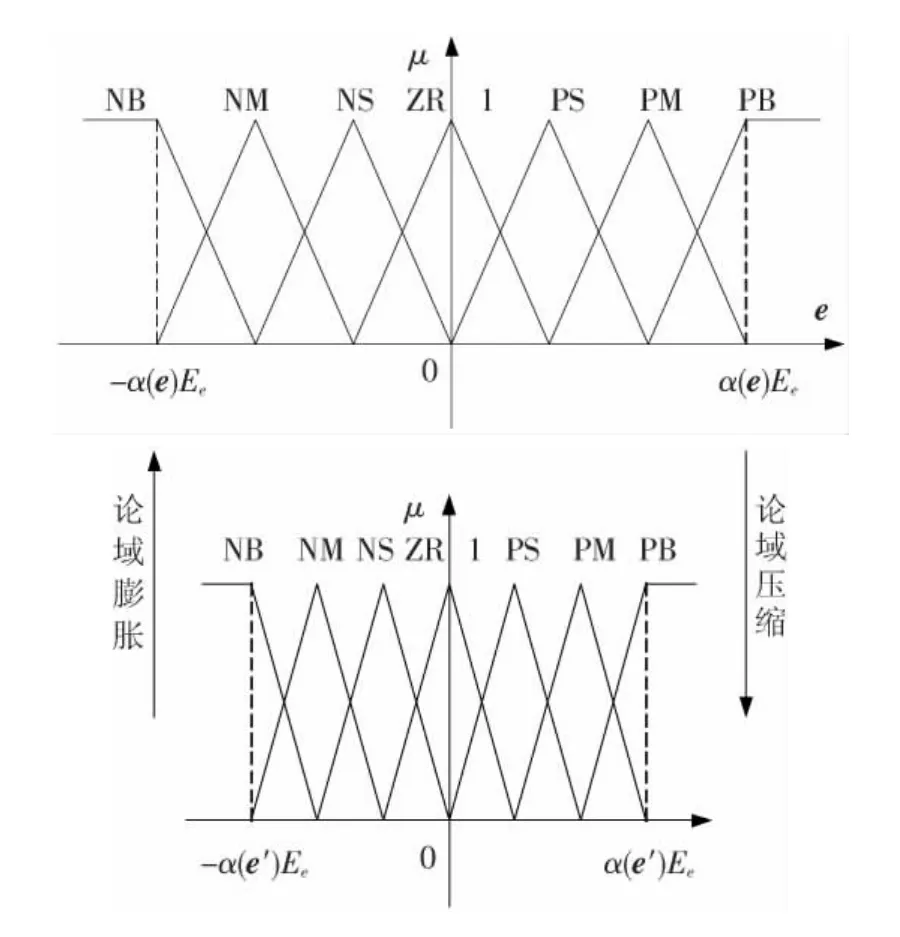
图2 论域的压缩与膨胀

目前常见的变论域模糊控制收缩因子有如下几种:

1)比例指数型收缩因子

2)自然指数型收缩因子

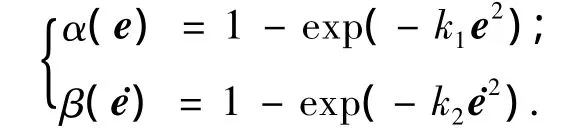
3)改进的自然指数型收缩因子

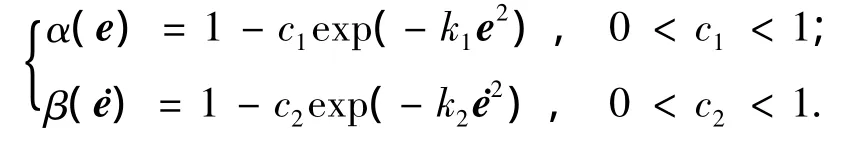
文献［10］研究了以上几种收缩因子的有效性，得出的结论是，这几种常见的收缩因子并不能使控制器的性能得到有效改善.为了解决收缩因子实时计算导致论域范围实时收缩，从而不能对控制器未来信号进行有效规范的问题，本文拟将改进的分形控制策略引入变论域模糊控制器.

2.2 分形控制策略

伸缩因子的实时计算将导致论域的实时收缩与膨胀，实时变化的论域不能对未来的输入信号进行规则约束，因此这种计算对控制系统的实现是一种极大的浪费.变论域的分形控制方法能够回避这种论域的实时计算，使所收缩的论域实用化.文献［11］提出了一种变论域分形控制方案，但这种分形方案是人为制定的，并且是有限次的.人为制定的分形方案只适合处理特定的系统，不具有普适性，有限次的分形只能让论域进行有限次的收缩，无法使作为模糊控制器数学本质的插值器的插值结点间的距离充分小，从而不能达到较高的插值精度，因此无法适合高精度控制的场合.

本文提出的分形方案的实施方法是，首先根据经验定义输入变量e和输出变量u的初始论域 分 别 为 ［- Ee0，Ee0］， ［- Eec0，Eec0］和［-U0，U0］，在程序运行过程中，当˙e=0，也就是误差量e达到1个极值时，系统自动进行一次分形，将当前误差量e1的绝对值作为输入量e的当前论域值，记为［-Ee1，Ee1］= ［-|e1|，|e1|］.

误差量变化率的论域记为

输出变量u的论域记为

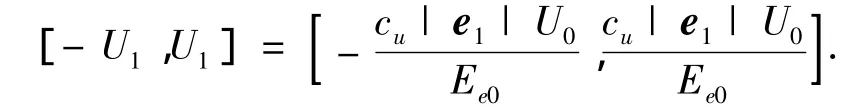
上式中下标1代表第一次分形，cec、cu是可调节的设计参数，分形完毕后程序继续运行直到再次出现˙e=0时，系统进行第二次分形，将此时的误差量记为e2，输入输出变量的论域分别调整为

以此类推，程序运行过程中，系统将进行无限次分形，直到论域足够小，控制精度达到要求为止.

本文提出的这种分形方案的优势体现在以下几个方面:

1)分形时刻，论域收缩或膨胀比例是根据输入误差量的变化情况而确定，非人为预先确定，针对不同的控制系统，具有一定的普适性;

2)无限次分形，可以使作为模糊控制器数学本质的插值器的插值结点间的距离充分小，插值精度可以满足事先任意给定的ε＞0，从而达到动态逐点收敛插值器的效果，适用于几乎所有高精度控制的场合;

3)将误差变化率和输出变量的论域变化与误差量论域的收缩与膨胀相关联，在控制规则不变的情况下，实现全局控制信息的多级缩微，真正达到多级粗控与精控相结合的控制效果，避免自适应控制中自适应律的繁琐推导与复杂的稳定性证明，同样可以实现具有一定鲁棒性的稳定的高精度控制.

仿真实验证明，在双输入单输出系统中，如果误差变化率与误差量的论域变化不关联，将会导致规则畸形，如果输出变量与误差量的论域变化不关联，将引起系统不稳定，这2种情况都将导致控制系统无法达到预期的控制效果.

3 数值仿真

为了验证本文提出的变论域分形控制策略的有效性，本节讨论1个柔性多体航天器大角度姿态机动问题.设航天器的初始姿态p0=［0.020 0.322 0.288］T，目标姿态与轨道坐标系重合，如果用欧拉角表示，按3-2-1的顺序转换姿态，则初始姿态为滚动角φ0=35°，俯仰角θ0=60°，偏航角 ψ0=50°，目标姿态为 φt= θt= ψt=0°，初始角速度 ω0= ［0.03 0.02 0.04］(°/s)，模态坐标及其变化率的初值选为零，航天器的转动惯量矩阵I，挠性附件与星体的耦合系数矩阵C，挠性附件模态阻尼系数矩阵ξ和频率矩阵Λ如下:

模糊控制器输入和输出的模糊子集数均为7，分别用 NB、NM、NS、ZR、PS、PM 和 PB 表示，由于线性和非线性隶属度函数对模糊控制效果的影响不大，且使用三角形隶属度函数具有计算方便、快捷的优点［12］，本文仿真中采用三角形隶属度函数，相邻模糊子集的重合度为0.5.表1为控制过程中使用的经典模糊控制规则库.

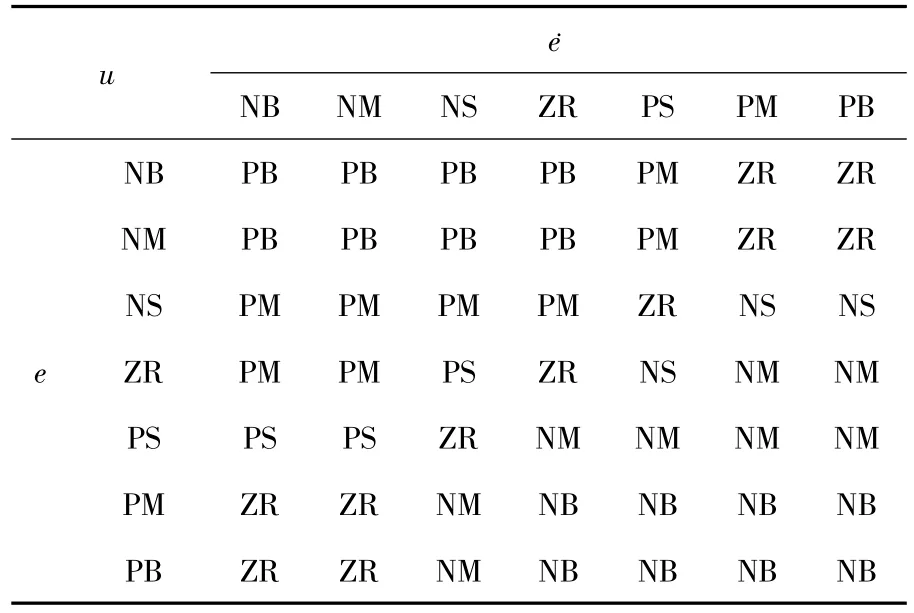
表1 模糊控制规则库

为了对比，同时给出固定论域控制器的控制效果，仿真结果如图3～6所示.图3～4给出了大角度姿态机动过程中，航天器姿态角和挠性附件模态坐标随时间的变化，以及当航天器惯量增加20%时的姿态角和模态坐标的控制效果.图5～6给出了在固定论域控制器的作用下，航天器姿态角和挠性附件模态坐标随时间的变化，以及惯量增加20%时的控制效果.

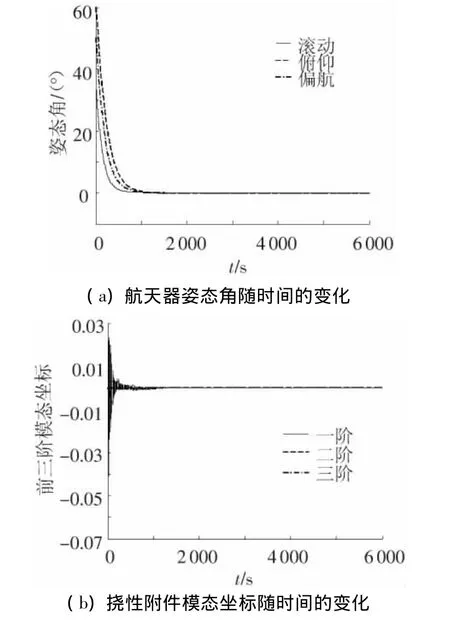
图3 变论域分形控制器的控制效果

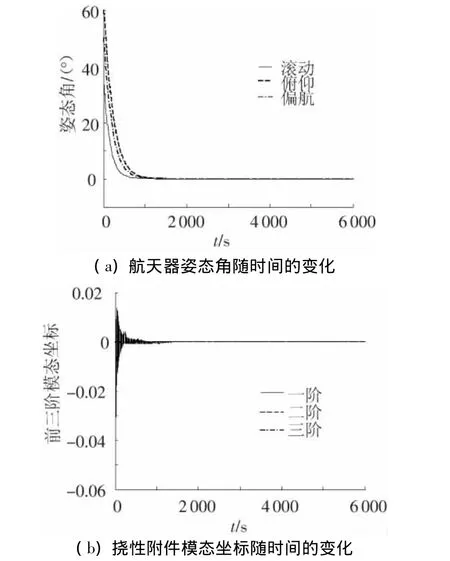
图4 航天器惯量增加20%时变论域分形控制器的控制效果

从运动学取2 000～6 000 s系统进入稳态后星体的实际姿态角及姿态角速率作为统计数据，计算出正常情况以及航天器惯量增加20%时两种控制器作用下的姿态控制精度和姿态稳定度的3σ值如表2所示.

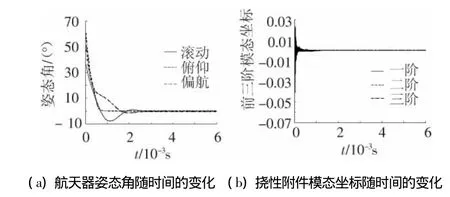
图5 固定论域控制器的控制效果

图6 航天器惯量增加20%时固定论域控制器的控制效果

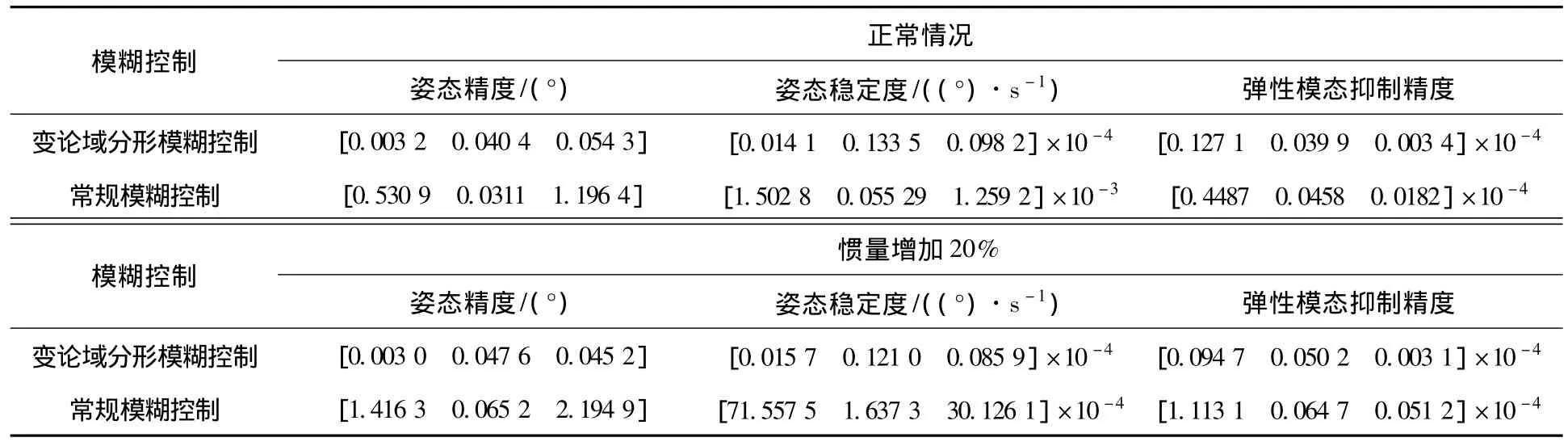
表2 姿态控制精度和姿态稳定度

从仿真结果中可以看出，变论域分形控制动态调节时间短，响应快，超调量小，稳态精度高，对惯量参数变化不敏感，能有效地抑制由于姿态机动引起的挠性附件振动，使航天器的姿态角得到较精确的控制，对航天器的模型不确定性具有良好的鲁棒性和适应性.

4 结论

本文针对柔性多体航天器大角度姿态机动问题，提出了一种变论域分形模糊控制方案.数值仿真结果表明，该方案回避了实时计算收缩因子所导致的论域范围实时收缩的缺点，有效的完成了对柔性多体航天器的大角度姿态机动控制，同时保证了航天器柔性附件的振动抑制，为柔性多体航天器姿态控制系统提供了一种有效、快速、稳定的控制方案.

［1］WIE B.Space vehicle dynamics and control［M］.Reston:American Institute of Aeronautics and Astronautics，1998:503 －583.

［2］YIGIT S A，ULSOY G A.Controller design for rigidflexible multibody systems［C］//Procceding of the 20 th Conference on Design and Control.Tampa，Florida:［s.n.］，1989:665 －673.

［3］NURRE G S.Dynamics and control of large space structures［J］.Guidance Control and Dynamics，1984，7(5):514－526.

［4］WANG L X.Stable adaptive fuzzy control of nonlinear systems ［J］.IEEE Transactions on Fuzzy Systems，1993，1(2):146－155.

［5］WANG L X，MATSUMOTO T.New time-domain stability criterion for fuzzy control systems［J］.IEICE Transactions on Fundamental of Electronic，Communications and Computer Sciences，1996，E79-A(10):1700－1706.

［6］WANG L X.Adaptive fuzzy systems and control，design and stability analysis［M］.Englewood Cliffs，New Jersey:Prentice-Hall，1994.

［7］司洪伟，李东旭.航天器刚柔耦合非线性系统的自适应变论域模糊控制［J］.航天控制，2007，25(5):28－32.

［8］CRASSIDIS J L，MARKLEY F L.Sliding mode control using modified rodrigues parameters［J］.Journal of Guidance，Control and Dynamics，1996，19(6):1381 －1383.

［9］李洪兴.从模糊控制的数学本质看模糊逻辑的成功［J］.模糊系统与数学，1995，9(4):1－13.

［10］潘湘飞，宋立忠.几种变论域模糊控制收缩因子有效性研究［J］.控制工程，2008，15(S1):106－108.

［11］徐静波，徐望人.变论域分形控制研究［J］.东华大学学报(自然科学版)，2004，30(4):4－7.

［12］KRUSE R，GEBHARDT J，KLAWONN F.Foundation of fuzzy systems［M］.UK:John Wiley＆ Sons，1994.

Variable universe fractal control of flexible multi-body spacecraft for large angle attitude maneuver

YANG Si-liang，XU Shi-jie

(School of Astronautics，Beijing University of Aeronautics and Astronautics，100191 Beijing，China，yangsiliang@sa.buaa.edu.cn)

The dynamic model of flexible multi-body spacecraft with topological tree configuration has been established based on the Lagrange＇s equations in terms of quasi-coordinates.The kinematics of the spacecraft is described by Modified Rodrigues Parameters(MRPs).For this time-varing uncertainty flexible multi-body spacecraft dynamic system，a modified fractal controller via variable universe of discourse was designed and the numerical simulation was done.The results show that this control scheme avoids the flaw caused by real-time calculating of shrinkable factors，realizes the effective control of flexible multi-body spacecraft for large angle attitude maneuver，and assures the vibration suppression of the spacecraft flexible appendages at the same time.

spacecraft guidance and control;flexible multi-body spacecraft;large angle attitude maneuver;variable universe of discourse;fractal control

V448.2

A

0367－6234(2011)11－0136－05

2010－05－19.

国家自然科学基金资助项目(10872028).

杨思亮(1983—)，女，博士研究生;

徐世杰(1951—)，男，教授，博士生导师.

(编辑 张 宏)