航天器姿态跟踪的几乎干扰解耦控制

李传江，郭敏文，2，马广富

(1.哈尔滨工业大学 控制科学与工程系，150001 哈尔滨，lichuan@hit.edu.cn;2.北京控制工程研究所，100190 北京)

航天器姿态跟踪的几乎干扰解耦控制

李传江1，郭敏文1，2，马广富1

(1.哈尔滨工业大学 控制科学与工程系，150001 哈尔滨，lichuan@hit.edu.cn;2.北京控制工程研究所，100190 北京)

研究了有界干扰力矩作用下航天器姿态跟踪的几乎干扰解耦控制问题.采用修正罗德里格参数(MRP)作为航天器的姿态描述.利用非线性系统中的微分几何理论，通过反馈线性化方法设计跟踪控制器，使得在实现姿态跟踪的同时，实现了对系统的几乎干扰解耦控制，即在L2增益意义下实现了从干扰到跟踪误差的影响任意小，并通过Lyapunov方法证明了干扰对跟踪误差的L2增益可以通过调节相关参数实现任意减小，同时保证了姿态跟踪误差系统是全局一致最终有界稳定的.最后进行数学仿真研究，验证了所设计的几乎干扰解耦控制器的可行性和有效性.

姿态跟踪;几乎干扰解耦;反馈线性化;Lyapunov方法;全局一致最终有界稳定

作为航天器系统诸多分系统的重要子系统之一，航天器姿态控制系统直接影响着卫星的工作性能和使用寿命.其实际在轨飞行时不可避免地受到空间各种环境力矩(如重力梯度力矩、太阳辐射力矩、气动力矩和地磁力矩等)和非环境力矩(如飞轮等执行机构的内部摩擦、航天器活动部件的转动以及执行机构的安装误差等)的作用.所有干扰力矩都会对航天器姿态控制性能产生一定影响，因此干扰力矩的抑制问题已经成为高精度高稳定度航天器姿态控制系统的重要研究内容之一.

干扰解耦控制，就是对给定的系统设计控制器，使得输出与干扰是无关的，但大多数的非线性系统不满足可干扰解耦的充要条件［1］，无法实现干扰解耦.针对此问题，相关学者提出了几乎干扰解耦控制［2］，即设计控制器使得在L2增益意义上干扰对输出的影响可以任意小.几乎干扰解耦问题首先在线性系统中提出并得到了基本解决，而在非线性系统中一直是研究的热点之一.国际上提出各种方法如逆最优控制［3］，非线性H∞控制［4-5］，H∞自适应模糊控制［6］以及反馈线性化和前馈神经网络相结合的控制方法［7］等，还有不少针对某些特殊的非线性系统［8-9］的研究方案，如文献［10］针对一类不确定时滞系统，根据线性矩阵不等式和代数Riccati方程设计了静态状态反馈控制器，实现系统的鲁棒H∞几乎干扰解耦，文献［2］则通过输出反馈实现了一类带不确定输入动态非线性系统的鲁棒几乎干扰解耦和镇定问题.

然而采用几乎干扰解耦控制思想解决航天器姿态控制问题的研究结果较少，几乎没有文献论述.本文基于非线性系统的微分几何理论中的相对阶概念，针对由修正罗德里格参数(MRP)描述的刚体航天器姿态跟踪误差运动模型，利用反馈线性化的方法设计跟踪控制器，实现了跟踪系统的几乎干扰解耦控制，即从有界干扰到姿态跟踪误差的L2增益可以通过调节相关参数实现任意地减小，并通过Lyapunov方法证明了姿态跟踪误差的全局一致最终有界稳定性.最后对姿态跟踪系统进行了数学仿真，结果表明了所提出方案是有效可行的.

1 航天器运动模型

刚体航天器的动力学方程为［11］

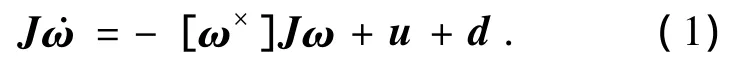
式中:ω=［ω1ω2ω3］T表示航天器本体坐标系相对于地心惯性坐标系且表示在本体坐标系上的姿态角速度向量;J∈R3×3为航天器的对称正定 转 动 惯 量 矩 阵;u=［u1u2u3］T、d=［d1d2d3］T分别表示航天器在轨飞行时的三轴控制力矩向量和所受干扰力矩向量;另外，对任意 l=［l1l2l3］T，定义叉乘算子［l×］如下:

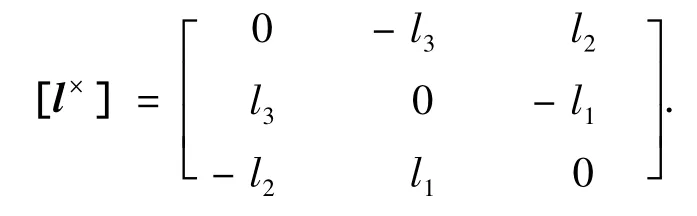
由MRP参数σ=［σ1σ2σ3］T描述的航天器非线性运动学方程为［12］

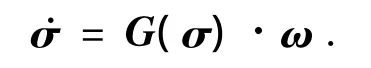
其中矩阵G(σ)∈R3×3定义如下:

式中In为n×n维单位矩阵，σ2=σT·σ.

G(σ)矩阵满足如下性质:

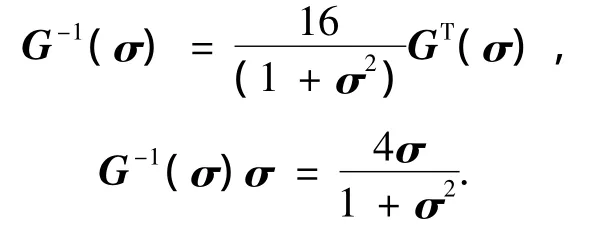
2 航天器姿态跟踪模型

令σd、σe分别表示惯性坐标系到期望坐标系的期望MRP向量和期望坐标系到本体坐标系的误差MRP向量.由σe表示的方向余弦矩阵R(σe)定义为

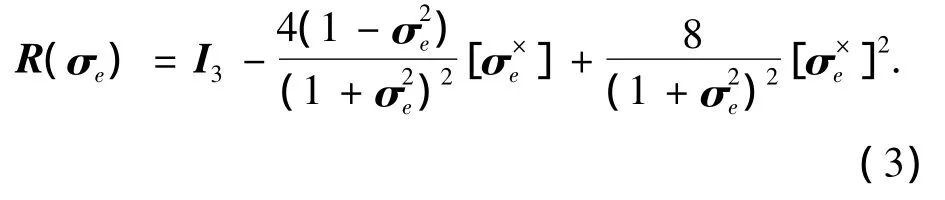
取ωd及ωe分别表示期望角速度向量和误差角速度向量，则在本体坐标系中有关系式

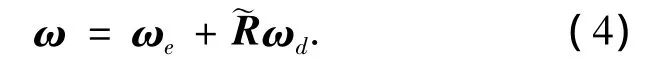
将式(4)代入式(1)，整理可得航天器的误差动力学方程为

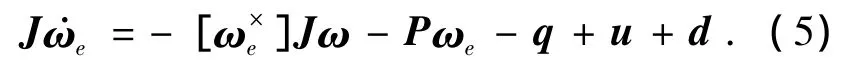
式中矩阵P和向量q定义如下:

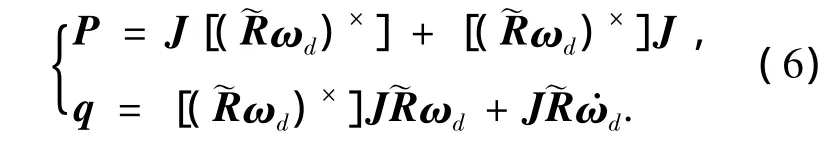
另一方面，由σe和ωe描述的误差运动学方程为

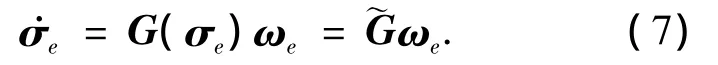
3 几乎干扰解耦控制设计

3.1 相关基础知识

定义1［12］(向量相对阶)仿射型m维输入m维输出非线性系统

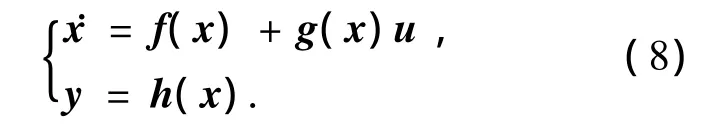
在x0处具有关于输入u的向量相对阶为{r1，r2， …，rm}，如果同时满足:

1)存在x0的一个邻域U，对其中所有x有ri-1，其中

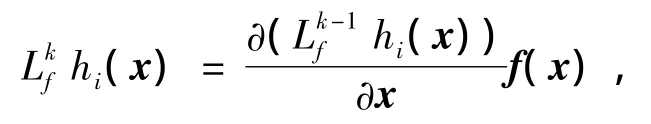
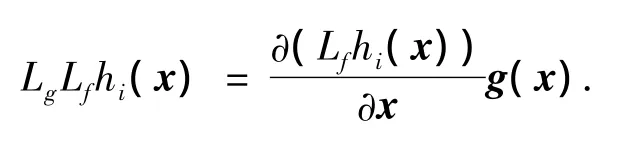
这里L为Lie导数.

2)m×m维矩阵

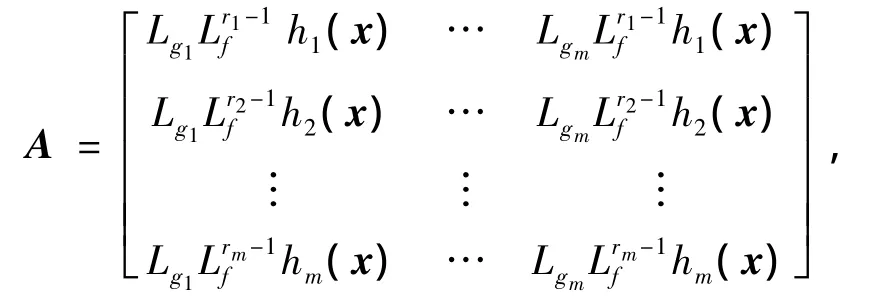
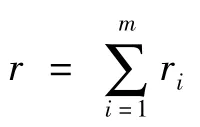
定义2［13］(K 类函数)连续函数 α:［0，a)→［0，∞)，如果满足:

1)α(0)=0;

2)α(p)＞0，∀p＞0;

3)α(·)是严格增函数;则称该函数为K类函数.

定义3［13］(KL类函数)连续函数β:［0，a)×［0，∞)，如果满足:

1)对于固定的s，β(γ，s)关于γ是K类函数;

2)对于固定的γ，β(γ，s)关于s为减函数;而且当s→∞ 时，有β(γ，s)→0成立，则称该函数β(·，·)为KL类函数.

定义4［13］(微分同胚映射)若存在1个连续可微的映射φ(x)，且对于所有的x∈U，其逆映射φ-1(φ(x))=x存在且光滑(也是连续可微的)，则称φ:U→Rn为U和Rn之间的1个微分同胚映射.

这里根据相对阶的概念，针对系统(8)定义1个全局微分同胚映射

为如下形式:

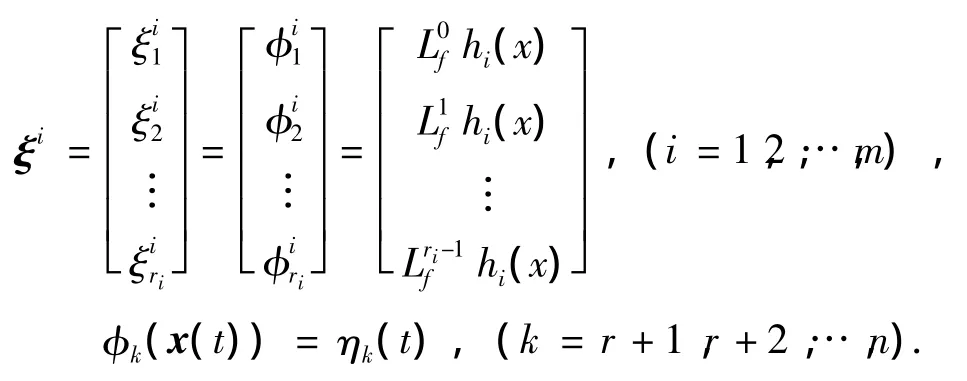
且满足

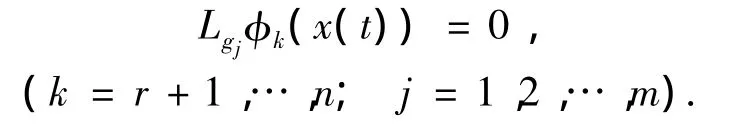
引理1［14］针对有界干扰d作用下的系统(8)，通过全局微分同胚映射(9)得到的误差系统，如果设计反馈控制器u满足如下要求:

1)系统是输入到状态稳定的;

2)对任意初始状态x(t0)，任意时刻t≥t0，有

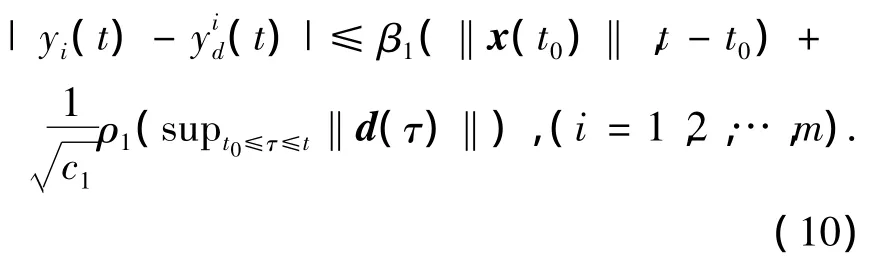
且

其中:c1、c2是正数;ρ1、ρ2是K类函数;β1是KL类函数;yd=［…］T为期望输出向量.那么称控制器u实现了输出跟踪和几乎干扰解耦控制.

3.2 控制器设计

取状态变量x=［］T，其中 x1=σe，x2=ωe，则航天器姿态跟踪方程(5)～(7)可写为如下三维输入三维输出方程:

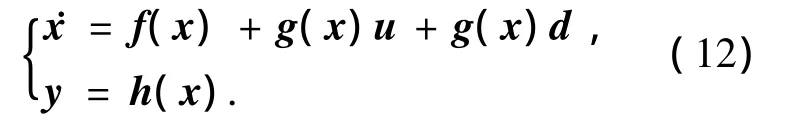
其中

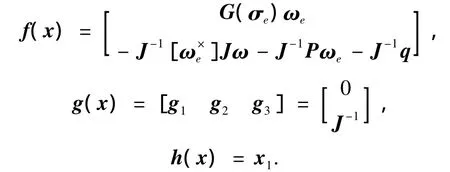
由定义1可以判定，系统(12)在平衡点x0=［0 0 0 0 0 0］T处具有向量相对阶{r1，r2，r3}={2，2，2}，进而可知跟踪系统总的相对阶为r=6，与跟踪系统的维数相等，因此系统可完全线性化，不存在内动态.

由映射(9)，引入如下坐标变换:

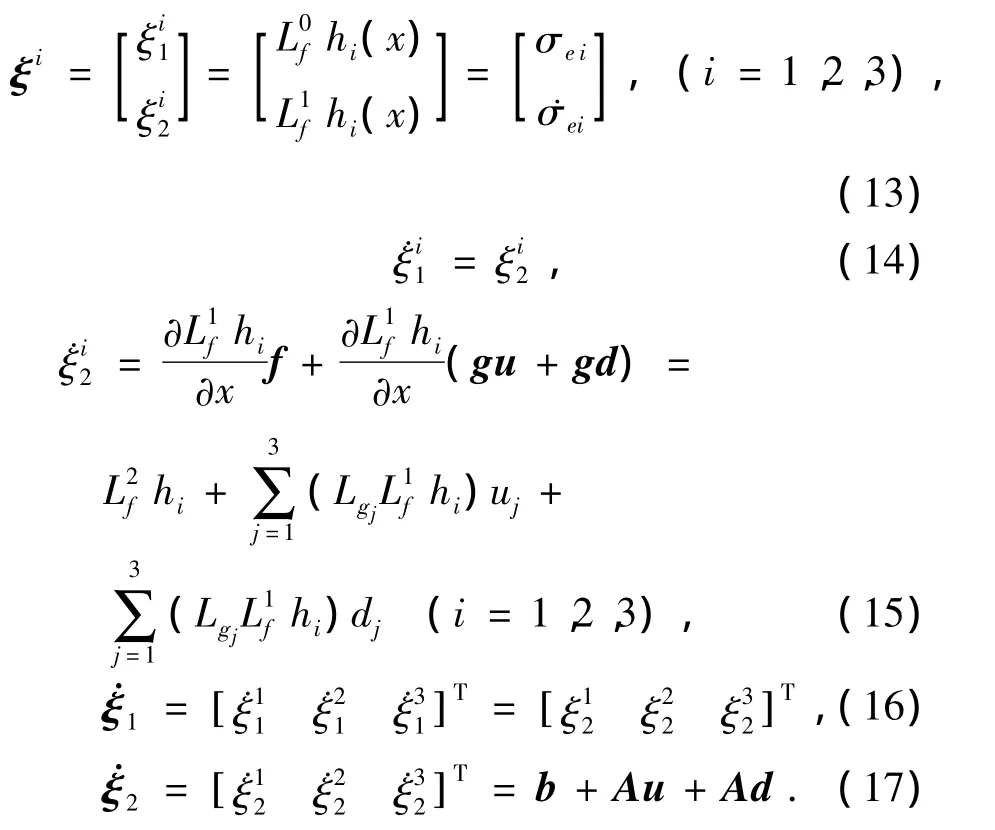
其中A，b定义如下:

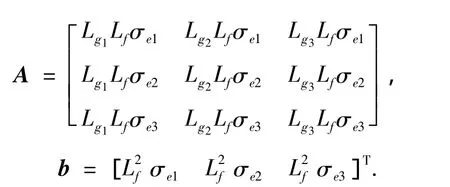
设计控制器u如下:

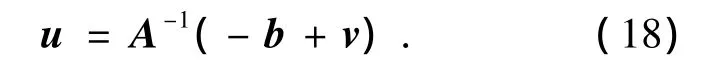
其中v=［v1v2v3］T为参考输入信号.

将式(18)其代入式(16)、(17)整理得到仿射型非线性系统(12)的线性化状态方程如下:

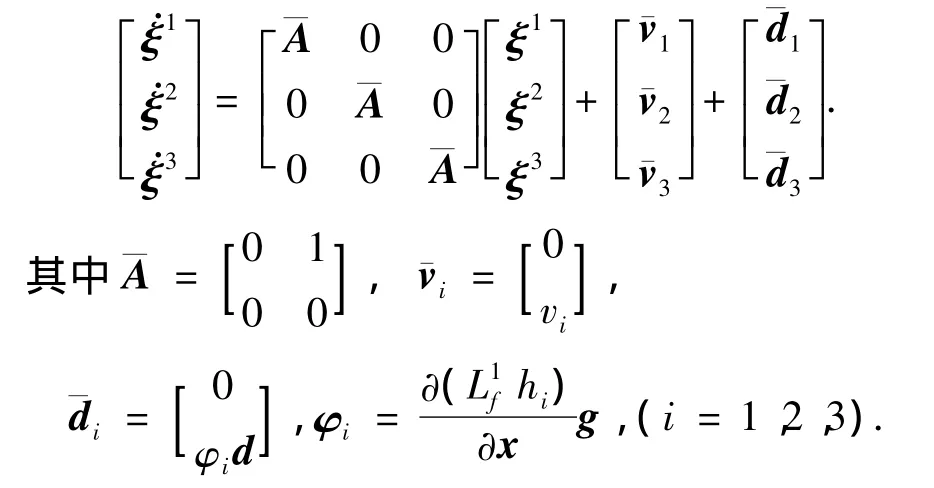
为分析问题方便，考虑第i(i=1，2，3)通道状态方程:

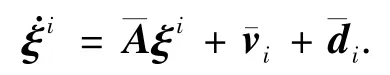
定义系统的姿态跟踪误差为:

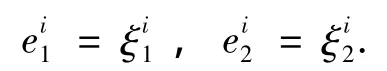
并将跟踪误差做如下变换:

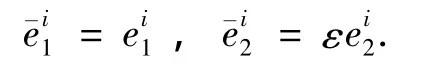
其中ε＞0为可调参数.同时令参考输入信号

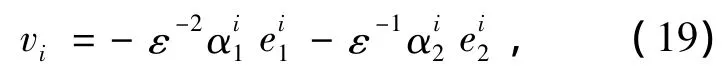
则得第i通道的线性化误差状态方程

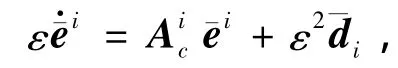
其中

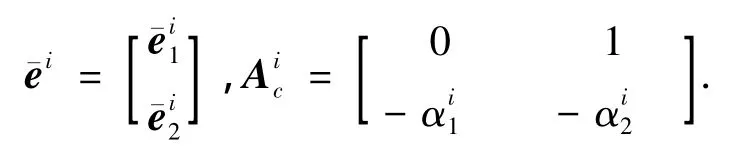
令λmin(Pi)、λmax(Pi)分别表示Pi的最小和最大特征值，取

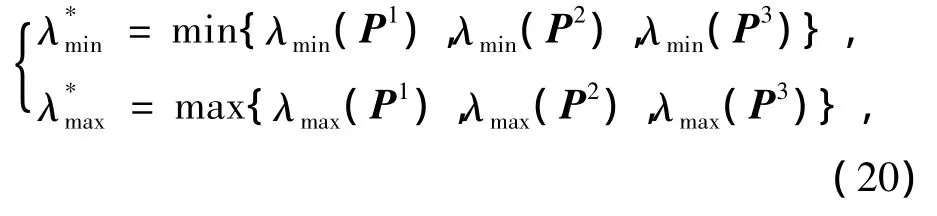
及正定Lyapunov函数V为

其中Vi=0.5(¯ei)TPi¯ei，k(ε)为R+→R+的任意连续函数，且满足

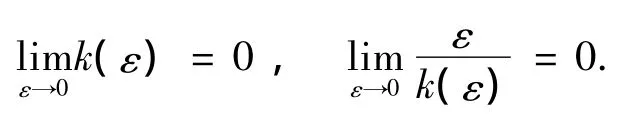
对式(21)求时间导数，可得

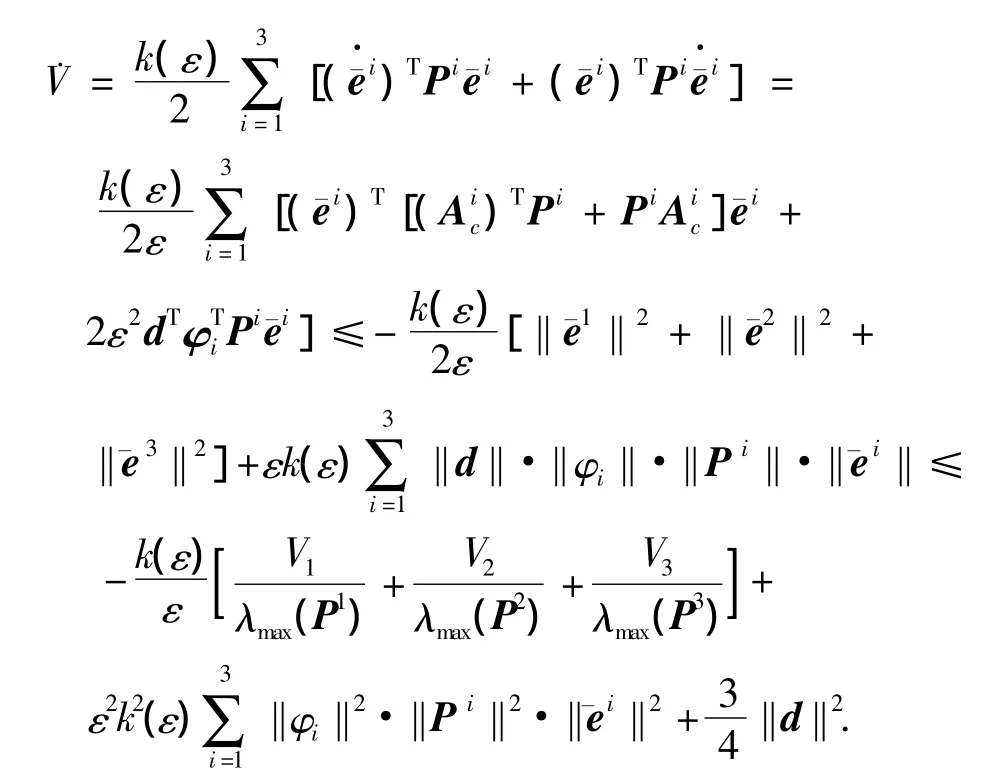
由式(20)、(21)易得

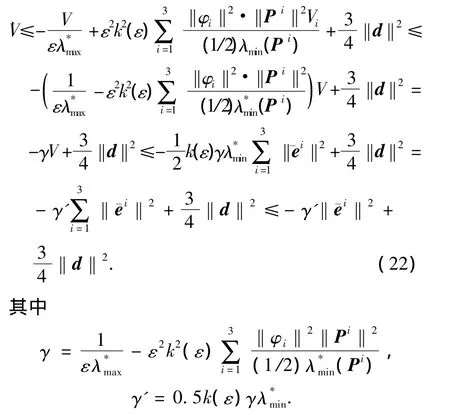
由上述结论可知

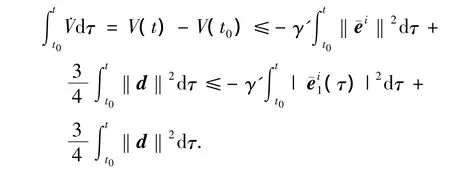
进而可得

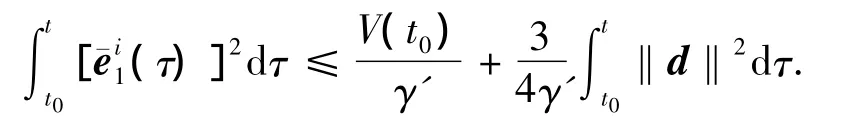
可见当γ＇＞0时满足式(11)，且可增大可调参数γ＇，实现跟踪误差任意减小.

另一方面，由式(22)可知

因此根据比较原理［15］得到

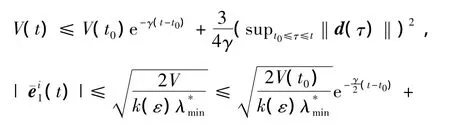
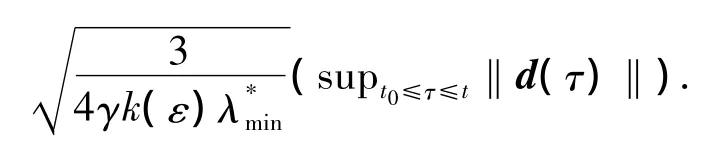
可见式(10)满足.

以上证明了干扰抑制下跟踪问题是全局可解的，最后，证明系统输出跟踪误差存在吸引域为球

由

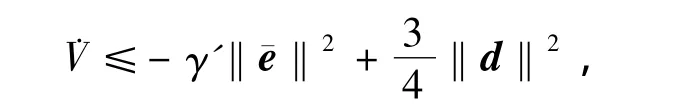
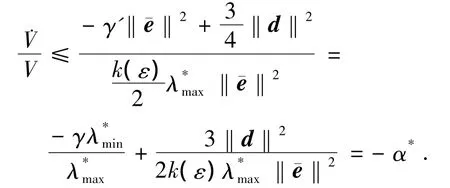
即˙V≤-α*V，根据比较原理［15］，得到V(t)≤V(t0)e-α*(t-t0)，因此

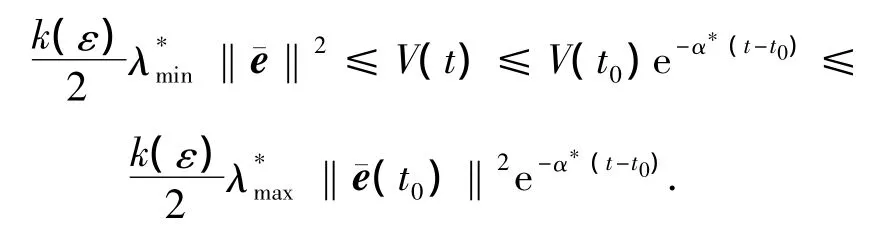
由此可得

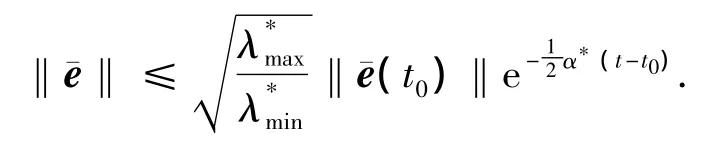
可见收敛至球域Br的收敛速率为0.5α*.整个过程证明了控制器实现了系统姿态跟踪的几乎干扰解耦控制.

为了得到关于误差状态ωe和σe反馈形式控制器，将控制器(18)进行如下的推导.由Lfh(x)=Lfσei=˙σei，可得

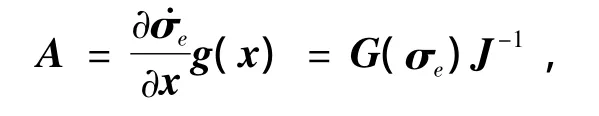
再由式(3)可得

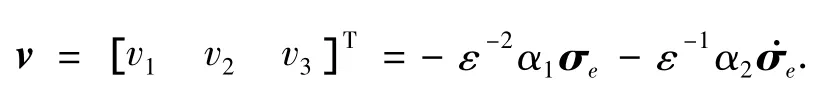
因此，

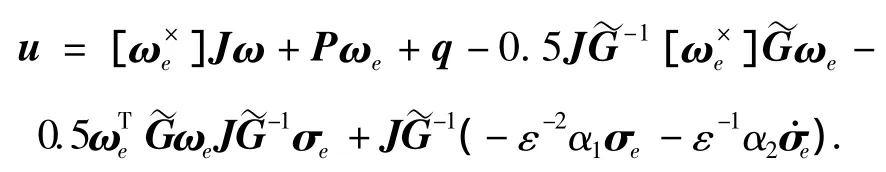
经过进一步推导，最终结果由如下定理给出.

定理1 考虑航天器姿态跟踪系统(5)～(7)，假设干扰d有界，那么如下跟踪控制器:

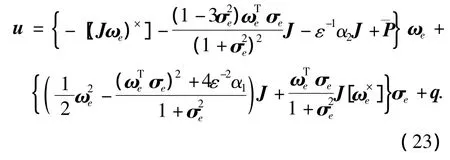
其中:ε，α1，α2均为正的常数，且

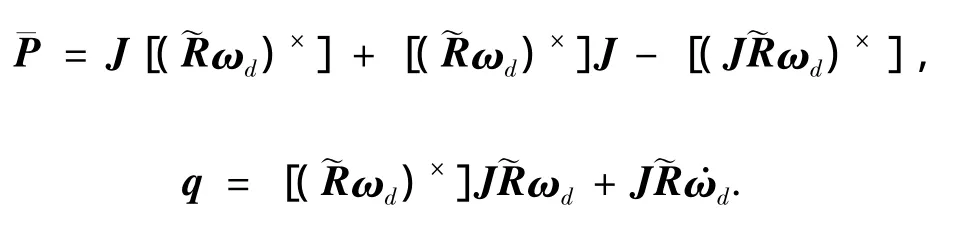
实现了闭环系统姿态跟踪的几乎干扰解耦控制，即干扰d对姿态跟踪误差的L2范数可通过调节控制参数任意地减小，同时保证了跟踪误差的全局一致最终有界稳定性.

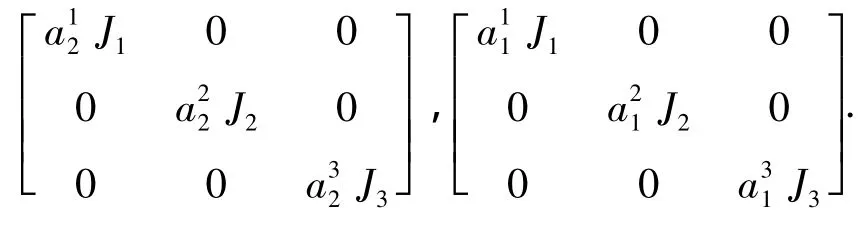
4 仿真分析

本节在Matlab/Simulink环境下对某航天器姿态跟踪系统进行了数学仿真，以验证所提出的几乎干扰解耦方案的可行性和有效性.

航天器的转动惯量取为

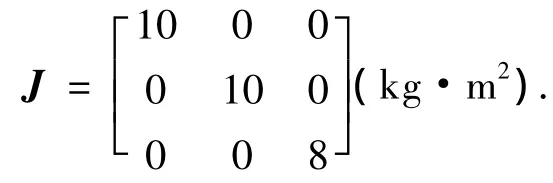
这里假设跟踪的目标角速度为

有界干扰力矩取为

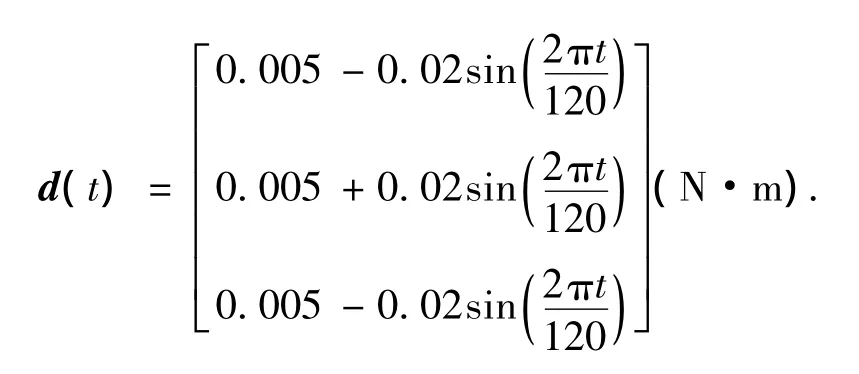
误差姿态的初始值取为

控制器参数取为

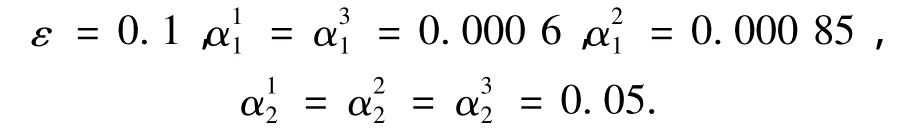
采用跟踪控制律(23)，得到仿真结果如图1～4所示.图1给出了实际姿态角速度和目标姿态角速度曲线;图2～3分别给出了角速度跟踪误差和姿态跟踪误差曲线;控制力矩变化曲线由图4给出.仿真结果表明，所设计控制器能较好地完成姿态跟踪任务，实现几乎干扰解耦，保证了闭环系统的跟踪误差是全局一致最终有界稳定的.

图5～图7给出了当控制器参数ε=0.05时的仿真结果，并将ε取不同值时的仿真结果进行比较分析.

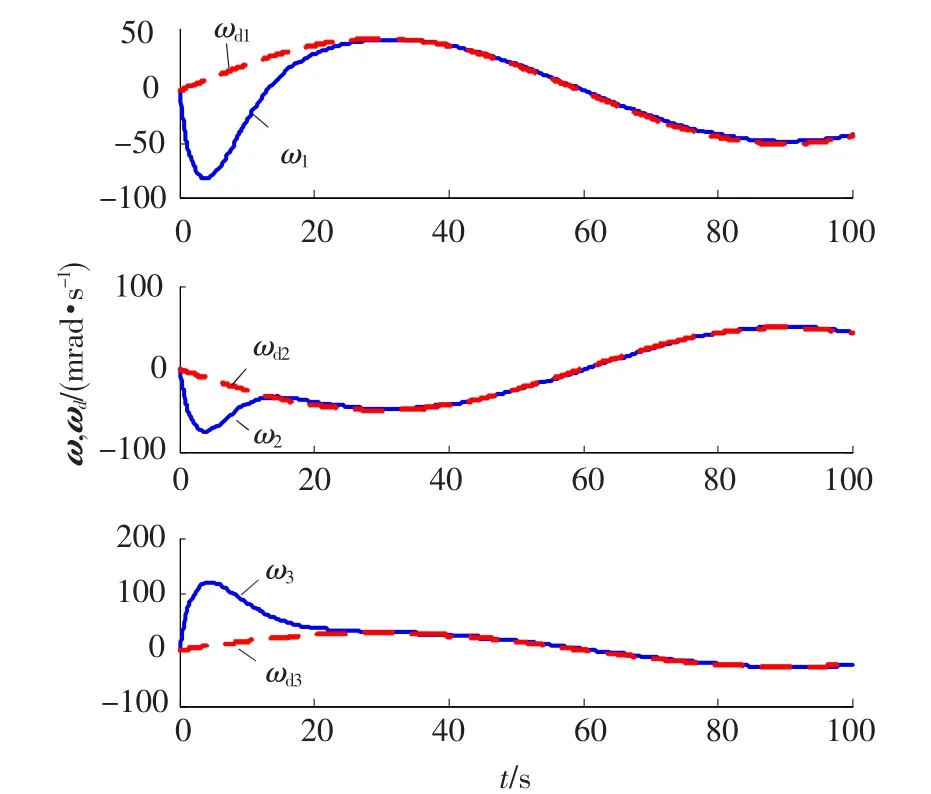
图1 实际角速度ω和目标角速度ωd(ε=0.1)

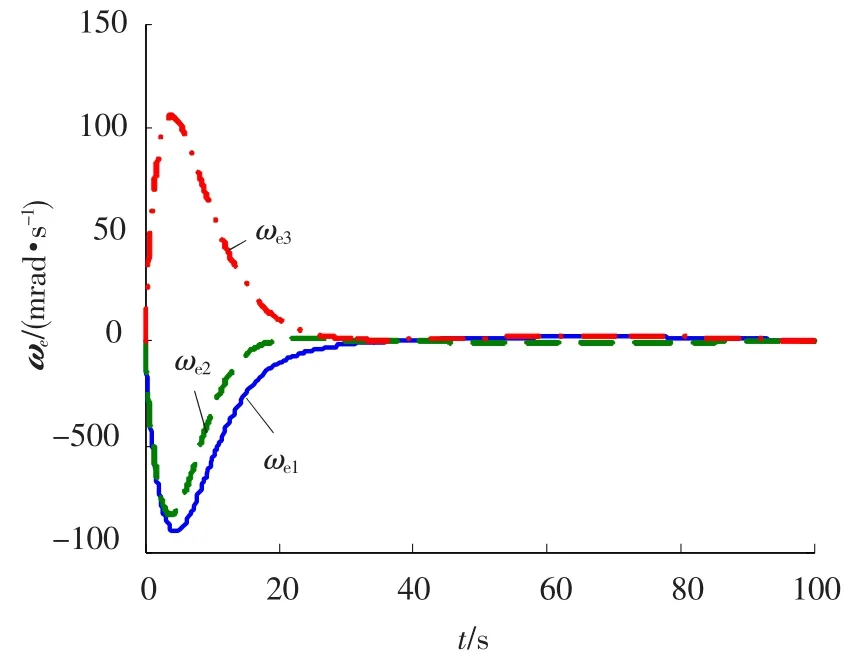
图2 角速度跟踪误差ωe(ε=0.1)

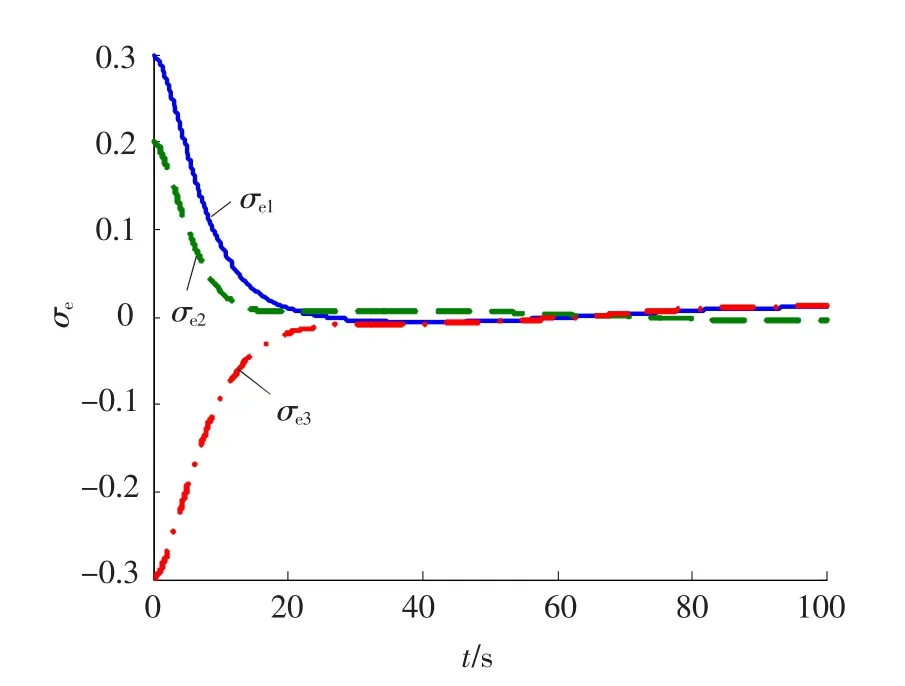
图3 姿态跟踪误差σe(ε=0.1)

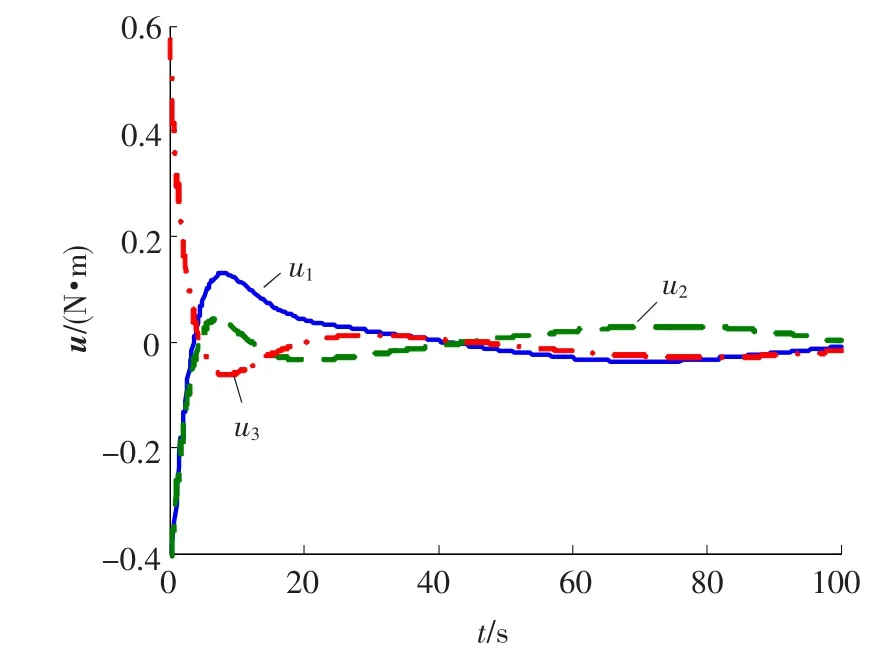
图4 控制力矩变化曲线(ε=0.1)

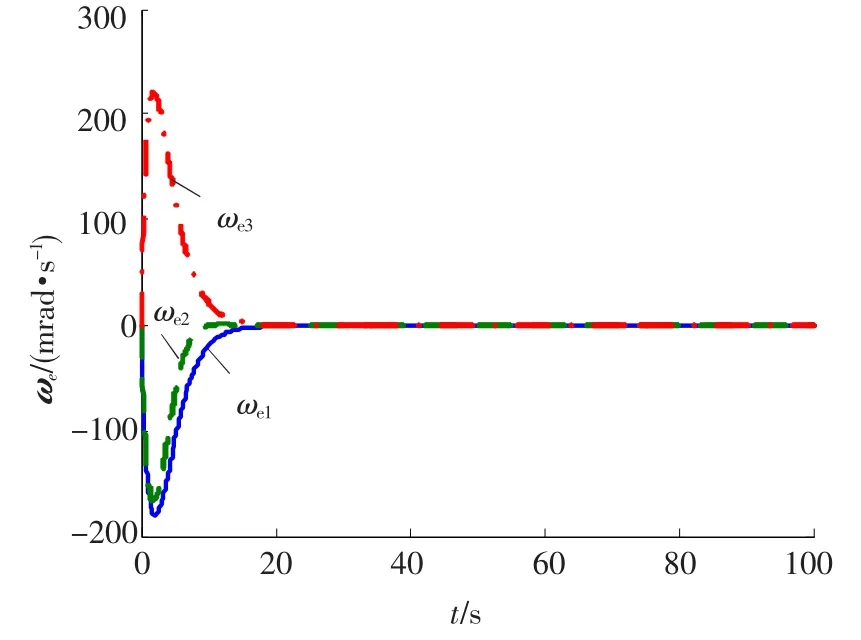
图5 角速度跟踪误差ωe(ε=0.05)

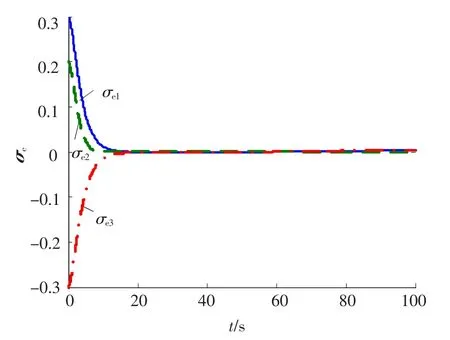
图6 姿态跟踪误差σe(ε=0.05)

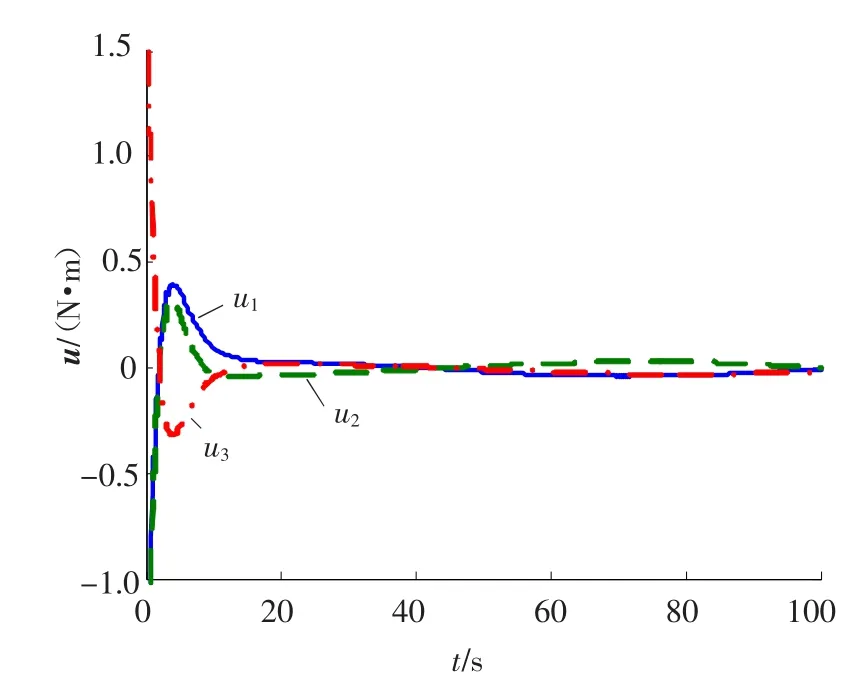
图7 控制力矩变化曲线(ε=0.05)

由图5～7可见，当ε减小为0.05时，姿态跟踪的角速度稳态误差和MRP稳态误差都较ε=0.1时有明显减小，但是相应的控制力矩u却随着ε的减小而增大，所以在实际系统中应根据执行机构所能提供力矩的能力，全面综合地选择控制器的参数，实现理想有效的姿态跟踪几乎干扰解耦控制.

5 结论

本文首先建立了带有干扰输入的航天器姿态运动误差模型，然后利用非线性微分几何理论中的反馈线性化方法设计控制器，并应用Lyapunov方法证明了该方法能够有效地实现系统的几乎干扰解耦控制，最终得到状态反馈形式控制器.根据系统输出跟踪误差的吸引域和收敛速度与调节参数ε之间的关系表达式，易知随着ε的减小，γ＇增大同时系统输出跟踪误差的吸引域减小，即稳态误差减小，且收敛速度也随着ε的减小而增大，这说明了干扰对跟踪误差的L2增益可以通过减小参数ε实现任意减小.仿真研究也通过比较两组不同的ε取值下的稳态误差值，验证了该结论.本文不足之处在于控制器依赖系统的转动惯量参数，因此设计自适应控制律实现对参数不确定性下姿态跟踪的几乎干扰解耦控制可作为后续的研究方向.

［1］王晓华，刘晓平.非线性广义时变系统的干扰解耦［J］.自动化学报，2000，26(6):798－802.

［2］王兴平，程兆林.输出反馈实现一类带不确定输入动态非线性系统的鲁棒几乎干扰解耦［J］.控制理论与应用，2004，21(2):183 －188.

［3］LUO Wengcheng，CHU Yunchung，LING Keck-Voon.Inverse optimal adaptive control for attitude tracking of spacecraft［J］.IEEE Transactions on Automatic Control，2005，50(11):1639 －1654.

［4］KANG Wei.Nonlinear H∞control and its applications to rigid spacecraft［J］.IEEE Transactions on Automatic Control，1995，40(7):1281 －1285.

［5］WANG Xinghu，JI Haibo.Stochastic H∞almost disturbance decoupling for a class of stochastic nonlinear systems［C］//Joint 48thIEEE Conference on Decision and Control and 28thChinese Control Conference.Shanghai:［s.n.］，2009:2887 －2892.

［6］CHEN B S，LEE C H，CHANG Y C.H∞tracking design of uncertain nonlinear SISO systems:adaptive fuzzy approach［J］.IEEE Transactions on Fuzzy System，1996，4(1):32－43.

［7］CHIEN Tingli，CHEN Chungcheng，HUANG Yichieh.Stability and almost disturbance decoupling analysis of nonlinear system subject to feedback linearization and feedforward neural network controller［J］.IEEE Transactions on Neural Networks，2008，19(7):1220 －1230.

［8］QIAN Chunjiang，LIN Wei.Almost disturbance decoupling for a class of high-order nonlinear systems［J］.IEEE Transactions on Automatic Control，2000，45(6):1208－1214.

［9］FU Yanming，WU Aiguo，DUAN Guangren.Almost disturbance decoupling for a class of inherently nonlinear systems［J］.International Journal of Control，Automation and Systems，2009，7(2):325 －330.

［10］陆国平，郑毓蕃.一类不确定时滞系统的鲁棒几乎干扰解耦问题［J］.控制理论与应用，2002，19(3):445－449.

［11］SIDI M J.Spacecraft dynamics and control［M］.Cambridge:Cambridge University Press，1997.

［12］宫清先，张化光，孟祥萍.一类MIMO非线性系统的稳定干扰解耦控制［J］.控制理论与应用，2006，23(2):199－203.

［13］ISIDORI A.Nonlinear control systems［M］.New York:Springer Verlag，1989.

［14］MARINO R，TOMEI P.Nonlinear output feedback tracking with almost disturbance decoupling［J］.IEEE Transactions on Automatic Control，1986，31:67 －69.

［15］KHALILl H.Nonlinear systems［M］.New York:Prentice Hall，2002.

Spacecraft attitude tracking based on almost disturbance decoupling

LI Chuan-jiang1，GUO Min-wen1，2，MA Guang-fu1

(1.Dept.of Control Science and Engineering，Harbin Institute of Technology，150001 Harbin，China，lichuan@hit.edu.cn;2.Beijing Institute of Control Engineering，100190 Beijing，China)

The problem of spacecraft attitude tracking under bounded disturbances is addressed based on almost disturbance decoupling.The modified Rodrigues Parameter(MRP)is adopted as attitude representation.A feedback linearization control scheme based on differential geometry for nonlinear systems is used to design the controller，by which the tracking and the almost disturbance decoupling performances can be easily achieved.Lyapunov theory is employed to prove that the influence of disturbances on theL2norm of output tracking error can be arbitrarily attenuated by changing some adjustable parameters in the controller，and that spacecraft attitude tracking system is globally uniformly ultimately bounded stable.Simulation results demonstrate the effectiveness and feasibility of the proposed control scheme.

attitude tracking;almost disturbance decoupling;feedback linearization;Lyapunov theory;global uniformly ultimately bounded stability

V448.22

A

0367－6234(2011)09－0007－07

2010－06－09.

国家自然科学基金资助项目(60774062);中国博士后科学基金资助项目(20070420858);哈尔滨工业大学优秀青年教师培养计划资助项目(HITQNJS.2008.006);哈尔滨市科技创新人才研究专项资助项目(2010RFQXG029).

李传江(1978—)，男，副教授;

马广富(1963—)，男，教授，博士生导师.

(编辑 张 宏)