高动态条件下改进的EKF载波跟踪环路

李思超，李金海，孙金海，汪峰，阎跃鹏

(中国科学院微电子研究所，北京100029)

高动态接收机主要涉及在高动态条件下对卫星导航信号进行捕获、跟踪及定位解算的技术．在高动态环境下，接收机的速度以及各阶导数值都较大，引起较大的多普勒频移，给伪码的捕获跟踪及后续的数据解调带来困难，为实现可靠通信，必须精确估计载波频移，并进行补偿．在未加辅助的条件下，高动态载波跟踪方法有最大似然估计(MLE)［1-2］、FLL/PLL［2-3］、自适应最小均方法(ALS)［4-5］、扩展Kalman 滤波器(EKF)［2，6］等．MLE 在 C/A 码延时 τ及多普勒频移ωd构成的二维坐标平面上求似然函数的最大值，以此来估计时延τ、多普勒频移ωd，估计精度高，但比较复杂，适用于超高动态目标的跟踪．FLL/PLL方法结构简单，计算量小，但是在高动态条件下需要采用高阶环路，将引起环路的稳定性问题［3］，在弱信号条件下，鉴别器的非线性将使得跟踪误差较大．ALS方法将接收信号进行泰勒展开得到观测方程，进而获得频率估计值，估计精度高，但结构也很复杂．EKF算法能够直接估计信号的相位、频率及其高阶导数，同时避免了鉴别器的非线性问题，跟踪性能好，灵敏度较高，高阶EKF计算量也较大，但是采用高性能处理器可以较好地解决这一问题．鉴于EKF的上述特点，本文以其为研究对象，对其环路带宽特性进行了理论分析，建立了相应的数学模型．根据分析结果，提出了一种改进的EKF载波跟踪算法．该算法比常规算法环路带宽窄，灵敏度更高．

1 EKF载波跟踪模型

EKF的跟踪过程与常规的DPLL类似，都是接收来自相关器的累加值，输出残差估计．图1为采用EKF的高动态GNSS跟踪环路，其中数据辅助模块为可选设置，为便于讨论，后续分析皆基于存在数据辅助．

图1 基于EKF的高动态跟踪环路Fig．1 High dynamic tracking loops based on EKF

为适应高动态条件，选择四阶EKF跟踪环路，其状态方程和量测方程为［2］

量测矩阵H可由下式得出［7］

EKF的迭代方程组为

式中:Q表示状态噪声协方差矩阵，α为加权系数，R为量测噪声协方差矩阵．

在NASA方案［2］中，每次迭代完成后，输入到载波NC0中的更新量为

式中:θk+1'、θk'为一步预测值．

2 EKF环路带宽特性分析

2．1 理论分析

由迭代方程组可知，EKF可以看作图2所示的负反馈环路．输入为量测值Yk，输出为状态估计值Xk，状态估计值的各个分量都来自相同的输入，具有相同的输入噪声功率谱密度．

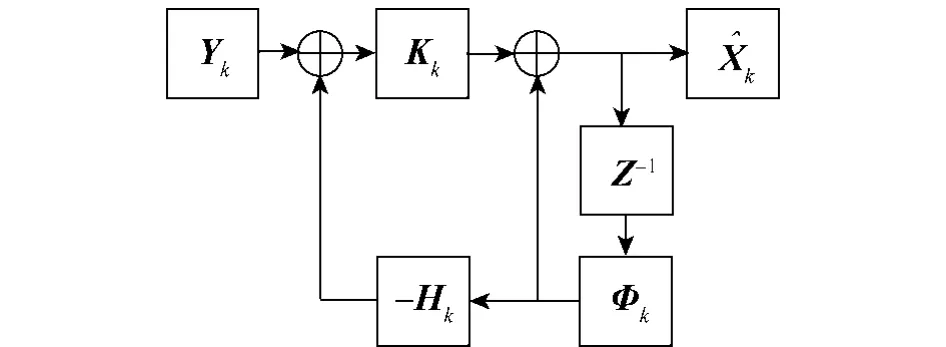
图2 EKF原理图Fig．2 Schematic diagram of EKF

NASA EKF方案的载波NC0更新量来自相位对于时间的导数，如式(3)所示．假设输入值的噪声功率谱密度为，对应相位一步预测值传输函数的等效环路带宽为Bp，则由相位差得到的频率更新量噪声功率为2Bp．若载波NC0的更新量由频率估计值提供(下称该方案 为 Modified EKF，即MEKF)，令对应频率估计值传输函数的等效环路带宽为Bf，则此时频率更新量噪声功率为Bf．若Bf＜2Bp，则以频率估计值更新NC0跟踪性能会有提高．

由EKF迭代方程组，得一步预测值为

对式(4)两端做Z变换，并整理得方程组:

式中:Mik(i=1，2，3，4)为在第 k次迭代时与 Pk'、a m^pk和a mpk有关的常量．

解方程组，得NASA方案中相位一步预测值的传输函数为

式中:aik、dik(i=1，2，3，4)为第 k 次递推时与Mik(i=1，2，3，4)有关的常量．

类似地，可得到MEKF方案中频率估计值的传输函数为

式中:aik、dik(i=1，2，3，4)为第 k 次递推时与 Pk'、am^pk和ampk有关的常量．

对于传输函数为H(z)的系统，其环路等效带宽为

将式(5)、(6)代入式(7)，可得NASA方案和MEKF 方案的等效环路带宽 BL，θ(k)、BL，ω(k)，其中的时间标度k表示第k次迭代时的值．显然，EKF的等效环路带宽与其参数有关，不是固定值．

由卡尔曼滤波器的稳定性原理［8］可知，无论滤波器初值如何设定，经过足够长的时间，卡尔曼滤波器都将达到稳态，此时Pk'→P'，并且满足Riccati方程［9］:

当EKF处于稳态时，等效环路带宽也趋于稳定．由Riccati方程可得 P'，代入式(5)～(7)，可得稳态环路带宽 BL，θ、BL，ω．EKF 的暂态过程存在不确定性，其解析解不易确定，可通过仿真得到暂态带宽．

2．2 仿真结果

采用文献［2］中提出的更为严格的高动态GPS信号，根据2．1节的分析结果，对2种方案的环路带宽特性做了仿真．中频频率的标称值为4．092 MHz，采样率为16．368 MHz，相干积分时间T=2 ms，采用2号卫星的PRN码进行扩频调制．

高动态信号的相对加加速度和相对加加速度特性示于图3．

可见，EKF的环路等效带宽经历暂态过程的波动后，逐渐趋于稳定，滤波器通过调整带宽完成了自适应滤波．稳态仿真带宽与通过Riccati方程计算的带宽差别极小，证明了理论分析是正确的．

图3 相对加速度和相对加加速度Fig．3 Relative acceleration and relative jerk

图4 环路带宽仿真值与理论值Fig．4 Loop bandwidth from simulation and theoreticalanalysis

图5(a)、(b)为在不同参数选择时2种方案的环路等效带宽．图5(a)α = 1．03分为108和107的2种情况;图5(b)=107，α 分为 1 ．02 和 1 ．03的2种情况．

图5 EKF稳态等效环路带宽Fig．5 Effective 100P banelwith of state of EKF

仿真时计算了NASA方案的2倍传输带宽2BL，θ．可见在各种条件下，MEKF的稳态传输带宽都满足BL，ω＜2BL，θ，MEKF 方案比 NASA 方案噪声功率要小．

此外，相比NASA方案，MEKF方案还可以减少两次向量相乘、一次减法和一次除法，计算量有一定的降低．

综上，选择MEKF作为高动态载波跟踪方案．

3 算法性能仿真结果

采用第2节的GPS高动态参数，对常规算法和MEKF算法进行了仿真测试．当频率误差超过奈奎斯特速率的1/2即250 Hz时认为系统失锁，失锁概率为10%的信噪比为门限信噪比［2］，可认为是跟踪灵敏度．

为便于比较，在仿真过程中取α=1．03、σ2j=4×104，与 NASA 方案［2］相同．图 6～8为载波频率及其一二阶导数的跟踪结果，信号强度为-150．5 dBm．可见，载波频率跟踪效果良好，频率的一、二阶导数跟踪结果抖动较大，但依然能够可靠地锁定．图9为改进前后2种方案频率估计均方根误差的仿真结果，图10为相应的失锁概率曲线，每一种测试条件进行了104次仿真，消除了随机性．表1列出了各种高动态载波跟踪算法在一定载噪比下的频率误差及各自的跟踪灵敏度［2］．

表1 性能统计Table 1 Cartogram of performance

图6 载波频率跟踪结果Fig．6 Tracking results of carrier frequency

图7 载波频率一阶导数跟踪结果Fig．7 Tracking results of first-order derivative of carrier frequency

图8 载波频率二阶导数跟踪结果Fig．8 Tracking results of second-order derivative of carrier frequency

当CN0≥24 dBHz时，2种算法的频率误差均方根相差不大，当CN0＜24 dBHz时，改进算法的性能较好;改进算法在失锁概率方面的优势是明显的．由表1可知，相同条件下MEKF算法的跟踪灵敏度比NASA算法提高了1．3 dB，频率误差也略有减小，其频率误差比其他方案小得多．这证明了MEKF算法的优越性及其理论分析的正确性．

图9 2种算法频率误差Fig．9 Frequency error of two algorithms

图10 2种算法失锁概率Fig．10 Probabilities of loss-of-lock of two algorithms

4 结束语

EKF的环路带宽具有自适应性，其稳态环路带宽是决定高动态跟踪性能的关键参数之一．通过对EKF环路带宽特性进行理论分析，建立了相应的数学模型，并进行了仿真，进而提出了一种改进的EKF高动态载波跟踪算法．与常规算法相比，改进后的算法减小了频率跟踪误差和失锁概率，提高了跟踪灵敏度．这对于提高高动态接收机性能有着重要的工程价值．下一步工作将研究如何充分利用EKF的所有状态估计值提高接收机的跟踪性能．

［1］HURD W J，STATMAN J I，VILNROTTER V A．High dynamic GPS receiver using maximum likelihood estimation and frequency tracking［J］．IEEE Transactions on AES，1987(4):425-436．

［2］HINEDI S，STATMAN J I．High-dynamic GPS tracking(final report)．JPL Publication 88-35［R］．［s．l．］，1988．

［3］STEPHENS S A，THOMAS J B．Controlled-root formulation for digital phase-locked loops［J］．IEEE Transactions on AES，1995(1):78-95．

［4］KUMAR R．Fast frequency acquisition via adaptive least squares algorithm［C］//Proeeedings of ITC．LasVegas，1986:155-160．

［5］HUMAR R．Differential sampling for fast frequency acquisition via adaptive extended least squares algorithm ［C］//Proceedings of the International Telemetering Conference．［s．l．］，1987:191-201．

［6］VILNROTTER V A，HINEDI S，KUMAR R．A comparison of frequency estimation techniques for high dynamic trajectories．JPL Publication 88-21［R］．［s．l．］，1988．

［7］李思超．高动态GPS接收机基带信号处理关键技术研究［D］．北京:中国科学院微电子研究所，2010:61．

LI Sichao．Research on key technology of baseband signal processing of HDGPS receiver［D］．Beijing:IME of CAS，2010:61．

［8］左启耀，袁洪，林宝军，等．基于Kalman滤波理论的高动态GPS信号跟踪系统仿真研究［J］．系统仿真学报，2009，21(8):2160-2164．

ZUO Qiyao，YUAN Hong，LIN Baojun，et al．Simulation research of high dynamic GPS signal tracking system based on Kalman filtering theory［J］．Journal of System Simulation，2009，21(8):2160-2164．

［9］SHALOM Y B，LI X R，KIRUBARAJAN T．Estimation with applications to tracking and navigation［M］．New York:John Wiley＆ SONS，inc，2001:349．