半监督聚类的匿名数据发布
杨高明,杨静,张健沛
(哈尔滨工程大学计算机科学与技术学院,黑龙江哈尔滨150001)
许多单位每天都在收集大量的个人信息,为从这些数据中得到有效的信息,需要应用数据挖掘技术.而数据挖掘技术的应用通常会导致个人隐私信息的破坏,为有效保护个人隐私,保留更多的有用数据信息,数据发布之前需要进行隐私保护[1-2].k-匿名[3]是隐私保护的数据发布技术常用模型,该模型把数据集划分成若干簇(组),使每个簇内至少包含k个元素,且簇内元组有相同的属性值.为使相同的簇内元组有相同的属性值,需要对元组进行概化/隐匿处理,该方法建立在预定义的域概化层次树结构和值概化层次树结构之上,因此会带来不必要的信息损失.为减少信息发布时的信息损失,不少学者研究使用聚类方法实现k-匿名[4-5].随着对k-匿名模型的研究深入,研究者发现k-匿名模型可以有效的抵御连接(link)攻击,但是不能抵御背景知识攻击和同质攻击[6].为防御背景知识攻击和同质攻击,学者研究了各种方法[6-8].其中l-多样性模型[6,9]要求每个簇类的敏感值要满足 l-多样性约束,以提高敏感值与其所属个体的链接难度,该模型使用概化/隐匿方法.王智慧等[10]提出使用聚类方法实现l-多样性隐私保护,他们首先对数据进行聚类,然后对聚类后的簇概化处理.p-敏感k-匿名模型[8]要求每个等价类中元组个数不少于k且敏感值种类不少于 p.(α,k)-匿名模型[7,11]通过控制等价类中敏感值出现的频率实现敏感值多样性.其中文献[11]提出(α,k)-匿名模型的概念,文献[7]使用概化方法予以初步完善.韩建民等[12]提出为(α,k)-匿名模型的每个敏感值设置一个α,这种方法适用于敏感值数目较少的情况,不适用敏感数值较多的情况,另外文献[12]不能处理数值属性,仅仅处理分类属性.
(α,k)-匿名模型目前有2种实现方法,即使用概化/隐匿方法[7]或者聚类方法[12].文献[7]给出了简单(α,k)-匿名和广义(α,k)-匿名概念和算法.聚类实现(α,k)-匿名方法[12]建立在文献[7]的基础上,扩展为每个敏感值设置一个比率上限α.对于敏感值较少的情况,文献[12]可以很好的实现隐私保护,若敏感值较多时,为每个敏感值设置上限就会变成费时费力的工作,而对于数据不断增长的情况则很难实现隐私保护工作.另外研究证明概化/隐匿方法实现k-匿名是NP难度的[13],且信息损失过大,数据效用(utility)低.为更好的实现隐私保护,降低信息损失,提高数据效用,提出半监督聚类的(α,k)-匿名模型,该模型为高敏感属性值提供较高的保护度,而低敏感属性值提供普通的保护度.
1 半监督(α,k)-匿名的相关概念
目前k-匿名及其演化的各种数据发布方法均把数据表属性分为3类:显式标识符属性、准标识符属性QI(quasi-identifier)以及敏感属性.显式标识符是惟一标识个体身份的属性,如用户身份证号码、姓名等.这些属性在数据发布前应被删除或加密;准标识符是通过这些属性的链接来标识个体身份的一组属性,如表1中属性组{Age,Sex,Country}.隐私保护的数据发布主要是改变准标识符属性,使个体的隐私信息不至于泄露;敏感属性指包含个体隐私信息的属性,如薪水、身体状况等,它们是数据发布中需要保护的属性.
定义1 给定数据表DT={A1,A2,…,Am,S},其中准标识符QI={A1,A2,…,Am},敏感属性为S.若存在一组元组,它们有相同的属性值{v1,v2,…,vm},则称它们为相对于准标识符 QI的等价类.
等价类包含元组数的多少标志着类中个体的身份保护强度,其包含的元组数越多,越难识别出等价类中的个体.如果一个数据集DT的每个等价类相对于QI包含的元组数大于或者等于k,则这个数据集是k-匿名的.例如表1中元组1、2、3、4关于{Age,Sex,Country}构成一个等价类,该数据表两个簇都满足4-匿名.满足k-匿名的数据表中每个元组被连接到具体个体的可能性减少了,个人的隐私信息得到保护.
k-匿名虽然可以很好的防止连接攻击,但是若攻击者发动同质攻击或者背景知识攻击,个人隐私依然会破坏.为提供更好的隐私保护效果,重新定义(α,k)匿名模型,即定义半监督(α,k)-匿名模型,同时避免了文[7,11-12]中的循环定义.
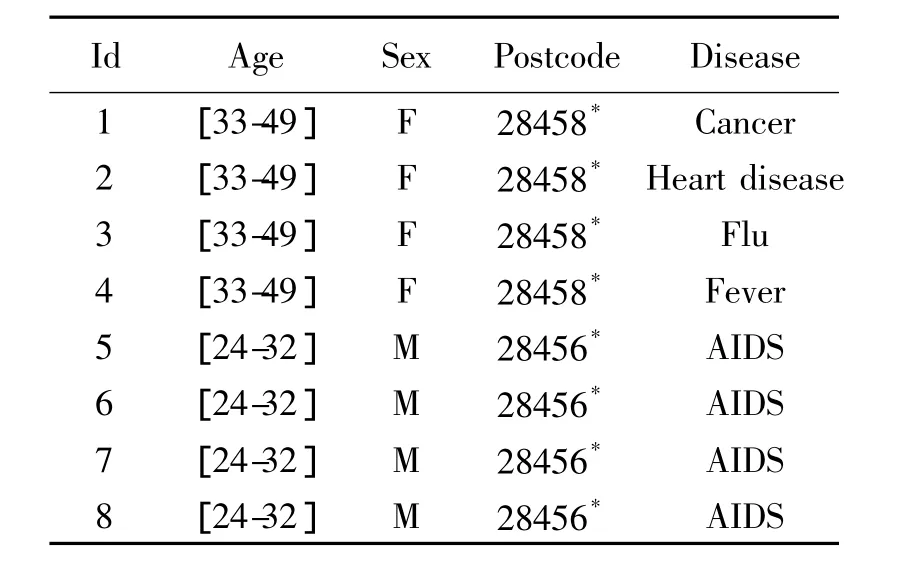
表1 匿名表Table 1 Anonymous table
定义2 给定数据表 DT={A1,A2,…,Am,S},其中准标识符QI={A1,A2,…,Am},敏感属性为S.设存在映射f(DT)→DT',使得DT'满足k-匿名.设Sh⊆S为需要保护的高敏感属性集合,设Sl⊆S为不需要特别保护的低敏感属性集合.若对∀s∈Sh,设(EC,s)为等价类EC中包含敏感值s的元组的集合,α(0<α<1)为用户指定的阈值.如果s在每个等价类中 的 频 率 都 不 大 于 α, 即 ∀EC, 都 有|(EC,s)|/|EC|≤α,则匿名数据表 DT'关于准标识符QI和敏感值s满足半监督(α,k)-匿名.
半监督(α,k)-匿名模型仅需为高敏感度值s设置一个频率约束α,要求等价类中高敏感值s∈Sh满足半监督(α,k)-匿名约束,而敏感度值s∈Sl不考虑其敏感保护度.敏感值s敏感性越强,则α值应越小.比如:AIDS的频率约束设为0.5,而Flu、Fever等常见疾病,它们的约束可以不考虑,则表2是满足这些参数的半监督(α,k)-匿名约束.
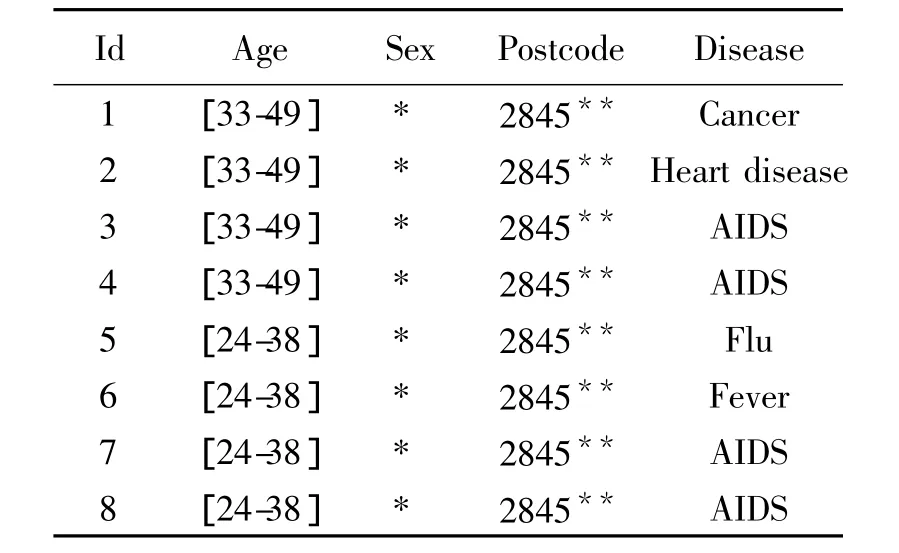
表 2(0.5,4)-匿名表Table 2 (0.5,4)-anonymous table
2 距离与数据效用度量
2.1 距离度量
数据集中的数据包含数值属性(连续型变量)和分类属性(离散型变量),处理这种数据最简单的方法是将这种混合型数据中的离散变量数值化;或者将连续型变量离散化,再分别利用相应的连续性或离散型聚类模型的建立方法来进行聚类分析.但是这2类方法都相应地抛弃了某些数据类型的特征,因而所得到的聚类效果并不好.更合理的混合型数据的聚类模型要充分考虑2类属性的特点,并能恰当地将两者结合起来.为达到更好的聚类效果,减少数据发布时的信息损失,本文引入度量空间映射方法,更详细的情况读者可以参考文献[14].
元组对象T在逻辑上可以表示为属性值对的逻辑“与”:[A1=x1]∧[A2=x2]∧…∧[Am=xm],此处 xj∈DOM(Aj),1≤j≤m.属性值对[Aj=xj]称为选择子,在不引起混淆的情况下以向量表示T.
假设数据集包含m个混合类型的变量,元组对象i和j之间的相异度d(i,j)定义为m
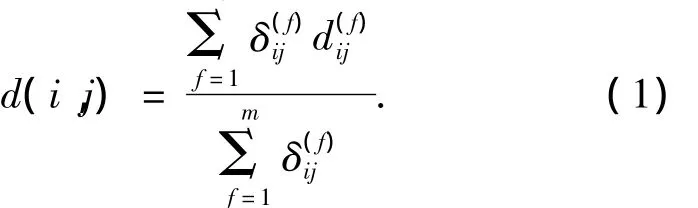
式中:如果xif或xjf缺失(即对象i或对象j没有变量f的度量值),或者xif=xjf=0,且变量f是非对称二元变量,则指示项=0;否则,指示项变量f对i和j之间相异度的贡献根据它的类型计算:
2)如果f是二元或者分类变量:如果 xif=xjf,
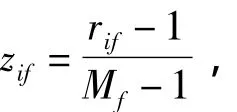
4)如果f是比例标度变量:要么进行对数变换,并且把变换后的数据作为区间标度的;要么把f当作连续的序数数据,计算rif和zif,然后把zif当作区间标度的数据来处理.
上面的步骤与各种单一变量类型的处理相同.惟一的不同就是基于区间的变量,其中规格化使得变量值映射到区间[0.0,1.0].这样,即便描述对象的变量具有不同类型,对象之间的相异度也能够计算.
2.2 匿名效用度量
聚类实现隐私保护的匿名化数据发布有2种发布方式:一种是发布簇中心和簇内的元组数和半径信息[4];一种是对每个簇进行概化/隐匿操作,并发布概化/隐匿以后的数据[10].本文采用概化/隐匿方法.
2.2.1 数值属性失真度
设数据表DT={A1,A2,…,Am,S},其中准标识符QI={A1,A2,…,Am}.元组t=(x1,…,xm)概化为 t'=([y1,z1],…,[ym,zm]),yi≤xi≤zi(1≤i≤m),则数值属性Ai的信息损失为

2.2.2 分类属性失真度
分类属性的概化通常伴随着分类层次系统树,它为属性值指定不同的粒度.设元组t在属性Ai上的值为v,概化为一系列值v1,v2,…,vm.它们在层次树上的公共祖先表示为ancestor(v1,v2,…,vm),则分类属性值的失真度为
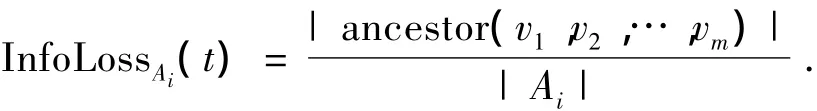
式中:|Ai|为在分类层次树上叶子结点数.
图1是分类属性Job和数值属性Age的分类层次系统树,依据分类层次系统树可以很容易计算出每个属性概化以后的信息损失.
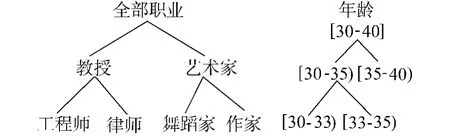
图1 Job和Age值泛化层次Fig.1 Value generalization hierarchies of Job and Age
2.2.3 元组和数据表的失真度
即包含数值属性又包含敏感属性的元组t,其信息损失为
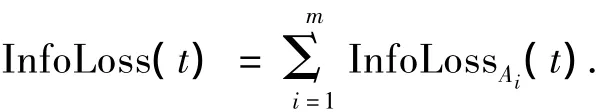
整个数据表的信息损失为

3 匿名模型的聚类算法
3.1 频率约束α的设置原则
设置敏感值的频率约束α应遵守以下2个原则:1)敏感性高的敏感值α应相对低些,敏感性低的敏感值,α应相对高些;2)α应该不小于该敏感值在原始数据表中的频率且α·k≥1,否则不能生成满足半监督(α,k)-匿名约束的匿名表.设DT为匿名表,|DT|为表中元组个数,E为一等价类,S为敏感属性,vs为一敏感值,α为vs的频率约束,则α应满足式:

3.2 算法描述
半监督(α,k)-匿名算法基本思想是:首先利用式(1)计算数据表的相异矩阵,由相异矩阵得到元组之间的两两距离,然后计算每个元组到其他元组的距离和,根据距离和选择质心点,距离和的计算使用式(2).由于相异矩阵中d(i,j)=d(j,i),所以相异矩阵是上(下)三角矩阵,根据该元组所在的对角线位置计算每个元组的距离和,把行和列上的距离相加即可.而选择距离最小的点做为质心主要是避免选择离群点做为质心点.利用质心点vi构造簇Ci并寻找距离簇Ci质心最近的个元组,若符合加入条件则加入簇Ci,直到簇Ci中元组数达到k.算法循环结束后在步骤10),若还有小于k的元组没有分配到等价类,则需要把这些元组分配到距离它们最近且满足(α,k)-匿名的等价类.算法描述见图2.
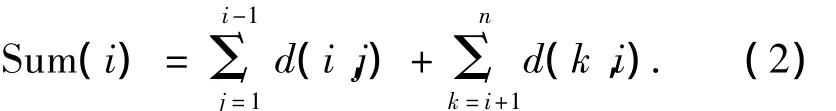
3.3 算法复杂度分析
算法步骤2)计算相异矩阵,其时间代价为O(n2).步骤4)计算每个元组的距离和Sum(i),其时间代价为O(n2).步骤5)~9)是一个循环过程,假设每个等价类都不小于k,则簇的个数至少为n/k.生成第1个簇的代价是O(k(n-(k+1)/2)),生成第2个簇的代价是O(k(n-(3k+1)/2)),生成第3个簇的代价是O(k(n-(5k+1)/2)),以此类推,直到第n/k个簇,所以聚类的平均时间花销为:O(O(k(n-(k+1)/2))+O(k(n-(3k+1)/2))+O(k(n-(5k+1)/2))+…+O(k(n-((2n/k-1)k+1)/2))=O(n2).算法步骤10)代价为O(k),k为剩余不能生成簇的元组.所以总的时间花销为 O(O(n2)+O(n2)+O(n2)+O(k))=O(n2).

图2 半监督(α,k)-匿名算法Fig.2 Algorithm of semi-supervised(α,k)-anonymity
4 实验数据及结果分析
4.1 实验数据及参数
实验主要分析半监督(α,k)-匿名的信息损失和执行时间.实验使用Adult标准数据集中的训练数据集,该数据集去除空值之后有30 162个记录.实验的硬件环境为 Intel Pentium IV 3.0GHz CPU,1GB RAM,操作系统为Microsoft Windows XP,编译环境是C++.为表示方便把半监督聚类(α,k)-匿名简称为 SemiAnony,把文献[7]的广义(α,k)-匿名简称为GeneAnony.本文比较它们的信息损失与时间代价.
4.2 信息损失分析
图3给出了k=25时,准标识符维数|QI|变化对GeneAnony和SemiAnony信息损失的影响,其中GeneAnony设置α=0.3,SemiAnony设置高敏感度属性α=0.3,低敏感度属性α=0.4.当准标识符维数|QI|增加时,GeneAnony和SemiAnony的信息损失均随之增加,在初始阶段增长较慢,随着|QI|数目的增加,GeneAnony明显比SemiAnony增长快.这主要是由于GeneAnony所有敏感值的α设置相同,且α大于所有敏感值在整个数据集的分布,所以其信息损失主要是由于随着|QI|的增加,需要概化更多的元组属性导致信息损失增大.由于每个属性值域大小不同,所以其信息损失幅度不同.随着|QI|的增加,SemiAnony需要处理更多的准标识符属性,因此其信息损失也呈增加趋势,但比起使用Apriori剪枝算法的GeneAnony增加趋势要小.在同等条件下,即当α、k和|QI|均相同时,SemiAnony的信息损失要远小于GeneAnony.这是因为GeneAnony使用Apriori剪枝概化策略,每次|QI|增加时,其上次的最优选择对下次选择来说不能保证仍然是最优的.而SemiAnony把属性值映射到相同的度量空间,采取聚类策略,同一个簇内的元组在相同度量空间上的距离一定最近,因此其信息损失也一定最小.

图3 准标识符维数|QI|变化下的信息损失Fig.3 Information loss when varying the size of|QI|
图4为|QI|=7,α=0.3,k值变化时,2种(α,k)-匿名模型信息损失量的比较.当k值较小时,等价类内的元组相似性较高信息较小,但此时的信息损失主要受α的限制,为满足(α,k)-匿名同一个等价类内的元组不一定是相似性最高的,因此总的信息损失仍然较大.随着k值的增大,α·k也随着增加,更容易生成满足(α,k)-匿名的等价类,这时α的影响减弱,k值影响增强.k的增加要求每个等价类中的元组数变多,要对元组进行更高层次的概化,所以信息损失会增大.由图4以及以上分析可知,总的信息损失先减少后增大.

图4 k变化下的信息损失Fig.4 Information loss when varying the size of k
由图3和图4以及上面的分析可知,相同情况下GeneAnony的信息损失量大于SemiAnony,因此SemiAnony匿名模型数据效用更强.
4.3 执行时间分析
图5给出了k=25,准标识符维数|QI|变化时对GeneAnony和SemiAnony执行时间的影响,其中GeneAnony设置α=0.3,SemiAnony设置高敏感度属性α=0.3,低敏感度属性 α =0.4.随着|QI|的增加,它们的执行时间都有所增加.但是GeneAnony的执行时间增长呈明显加速趋势.SemiAnony的执行时间初始状态大于GeneAnony,随着准标识符属性的增加,GeneAnony的执行时间逐渐超越SemiAnony.这主要是由于GeneAnony通过递增地考察准标识符子属性集上的概化属性值组合来寻找可实现广义(α,k)-匿名保护的概化方案,在最坏情况下广义(α,k)-匿名的执行时间随着准标识符维数增加将呈指数式增长,每个属性的维数和数据分布不同,所以增长的趋势不同,有增长快慢差异.而半监督(α,k)-匿名通过考察元组与类之间以及类与类之间的距离寻找合适的概化方案,以较小的信息损失来满足匿名保护的需求,其执行时间随着准标识符维数的增加而呈线性增长趋势.另外半监督(α,k)-匿名并不调整全部敏感属性值,仅调整高敏感属性值,k变大,聚类的次数变多,所以时间花销就会变大.
图6给出了当准标识符维数|QI|和固定,k值变化时对广义(α,k)-匿名和半监督(α,k)-匿名执行时间的影响.广义(α,k)-匿名模型随着k的增加执行时间增大,而半监督随着k值的增加反而减少.这种现象主要是由于广义(α,k)-匿名在准标识符QI的每个子属性集上采取Apriori剪枝概化策略.随着k值的增加,它需要作更多次概化尝试,直到概化处理结果满足广义(α,k)-匿名模型需求,所以k值增加使其执行时间有增加的趋势.对于半监督(α,k)-匿名来说,初始阶段需要计算相异矩阵和每个元组的距离和,簇质心点的生成和调整以及簇的生成,所花费的时间较短.而随后加入元组到类中,则需要多次进行距离计算来找到距离最小的元组或类,因此所花费的时间较长.因此当k较小时,半监督(α,k)-匿名的总体执行时间随着k值的增加而减少.
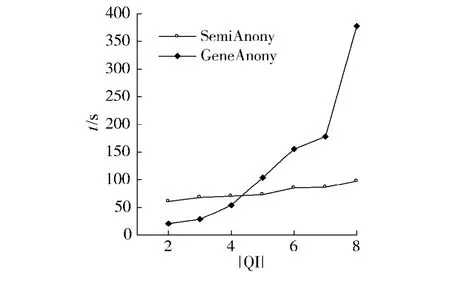
图5 准标识符维数|QI|变化时执行时间Fig.5 Execution time when varying the size of QI
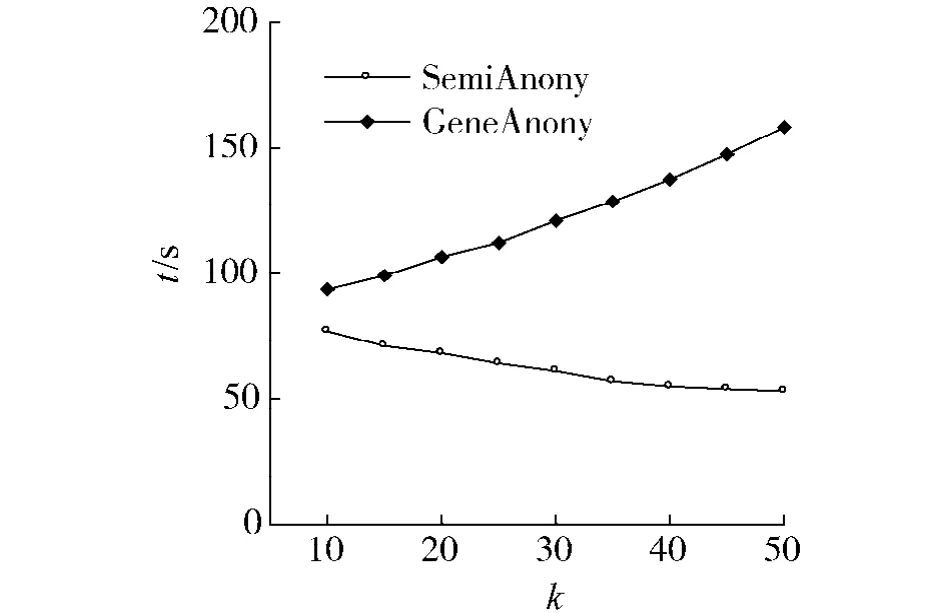
图6 k值变化下的执行时间Fig.6 Execution time when varying the size of k
由图5和图6以及上面的分析可知,在相同情况下,半监督(α,k)-匿名算法时间花销比广义(α,k)-匿名小.所以半监督(α,k)-匿名模型在时间代价提升的同时获得更好的隐私信息保护.
5 结束语
本文提出一种半监督聚类的(α,k)-匿名模型.针对数据集包含数值属性和分类属性的特点,为实现半监督聚类引入数据映射方法,使数值属性和分类属性在一个共同的度量空间运算.通过把敏感值分为高敏感度和低敏感度,实现了敏感值的个性化保护.实验结果表明,半监督(α,k)-匿名模型能够以与其他(α,k)-匿名模型近似的信息损失量和时间代价,获得更好的隐私信息保护.
[1]FUNG B C M,WANG K,CHEN R,et al.Privacy-preserving data publishing:a survey of recent developments[J].ACM Comput Surv,2010,42(4):1-53.
[2]CHEN B,KIFER D,LEFEVRE K,et al.Privacy-preserving data Publishing[J].Found Trends databases,2009,2(1):1-167.
[3]SWEENEY L. k-anonymity:amodelforprotecting privacy[J].International Journal of Uncertainty Fuzziness and Knowledge Based Systems,2002,10(5):557-570.
[4]AGGARWAL G,PANIGRAHY R.Achieving anonymity via clustering[J].ACM Trans Algorithms,2010,6(3):1-19.
[5]LIN J,WEN T,HSIEH J,et al.Density-based microaggregation for statistical disclosure control[J].Expert Systems with Applications,2010,37(4):3256-3263.
[6]MACHANAVAJJHALA A,KIFER D,GEHRKE J,et al.l-diversity:privacy beyond k-anonymity[J].ACM Transactions on Knowledge Discovery from Data,2007,1(1):1-52.
[7]WONG R,LI J,FU A,et al.(α,k)-anonymous data publishing[J].Journal of Intelligent Information Systems,2009,33(2):209-234.
[8]CAMPAN A,TRUTA T M,COOPER N.P-sensitive k-anonymity with generalization constraints[J].Transactions on Data Privacy,2010,3(2):65-89.
[9]MACHANAVAJJHALA A,GEHRKE J,KIFER D,et al.ldiversity:privacy beyond k-anonymity[C]//22nd International Conference on Data Engineering.Atlanta,GA,US,2006:24.
[10]王智慧,许俭,汪卫,等.一种基于聚类的数据匿名方法[J].软件学报,2010,21(4):680-693.
WANG Zhihui,XU Jian,WANG Wei,et al.Clusteringbased approach for data anonymization[J].Journal of Software,2010,21(04):680-693.
[11]WONG R,LI J,FU A,et al.(α,k)-anonymity:an enhanced k-anonymity model for privacy preserving data publishing[C]//Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.[s.l.],2006:754-759.
[12]韩建民,于娟,虞慧群,等.面向敏感值的个性化隐私保护[J].电子学报,2010,38(7):1723-1728.
HAN Jianmin,YU Juan,YU Huiqun,et al.Individuation privacy preservation oriented to sensitive values[J].Acta Electronica Sinica,2010,38(7):1723-1728.
[13]BAYARDO R J,AGRAWAL R.Data privacy through optimal k-anonymization[C]//Proceedings of the International Conference on Data Engineering.Tokyo,Japan,2005:217-228.
[14]HUANG Z.Extensions to the k-means algorithm for clustering large data sets with categorical values[J].Data Mining and Knowledge Discovery,1998,2(3):283-304.

