Sobolev方程各向异性非协调混合元的超逼近分析

白春阳,石东伟

（河南科技学院,河南新乡453003）

Sobolev方程在流体穿过裂缝岩石的渗透理论、土壤中湿气的迁移、不同介质的热传导等许多物理问题中有广泛的应用[1-6].其中文献[1]建立了特征混合元方法,并分别讨论了收敛性和误差估计.文献[2]仅对一维Sobolev方程提出了位移有限元法.文献[4]提出了相应的最小二乘混合元方法,该方法虽然不要求有限元空间满足LBB稳定性条件,但计算量大.文献[5]提出H1-Galerkin混合有限元方法,虽不要求有限元空间满足LBB条件,但对通量函数的光滑性要求更严格.文献[6]研究了几组简单的低阶协调元,给出了半离散格式和全离散格式的误差估计.但是以上研究都是针对协调元进行的,而且要求剖分满足正则条件,即,其中是单元K的最大直径单元K的最大内切圆直径.然而当问题定义在窄边区域时,如果采用传统的正则剖分计算量将会非常大,这时如果采用各向异性网格剖分可以用较少的自由度而得到同样的估计结果.在这种情况下,传统的引理在插值误差分析中已不再适用,而且对于非协调元来说传统边界估计技巧也不再适用,因为此时对单元K的长边F误差值估计将出现一个因子,它可能趋于无穷,无法达到收敛结果.本文给出了与以上文献不同的Sobloev方程的非协调混合有限元格式,在各向异性网格下进行了收敛性分析,并利用单元自身的一些特殊性质得到了超逼近结果,同时利用插值后处理技巧导出了超收敛结果.

1 单元构造

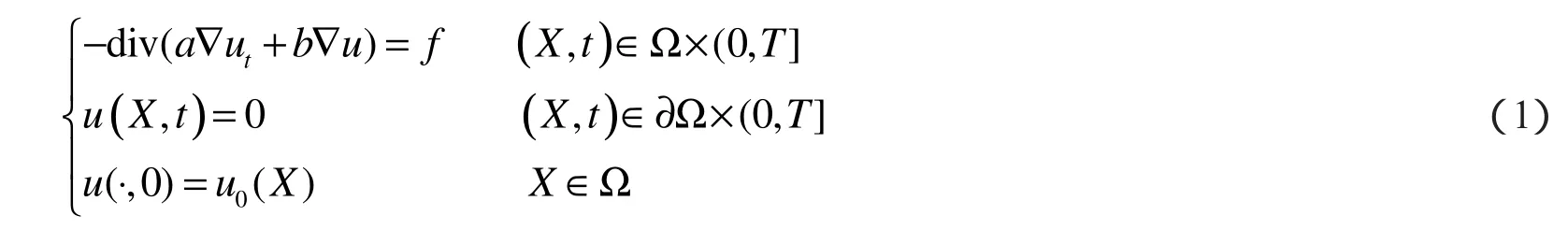
使得

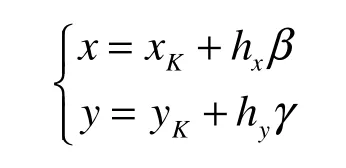
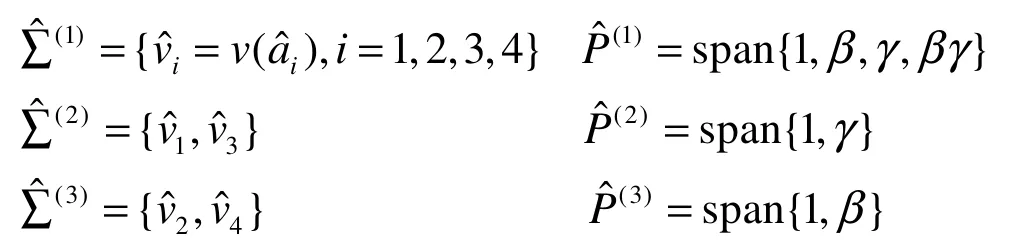
由文献[7]不难验证上述插值具有各向异性.

2 误差估计

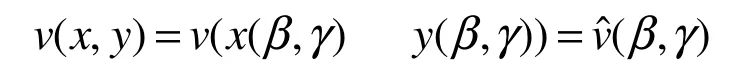
相应的有限元空间为：

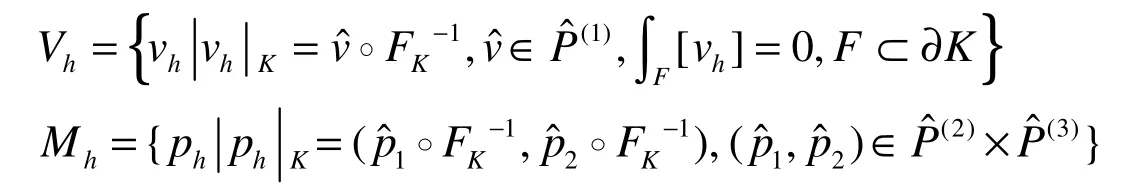
定义插值算子

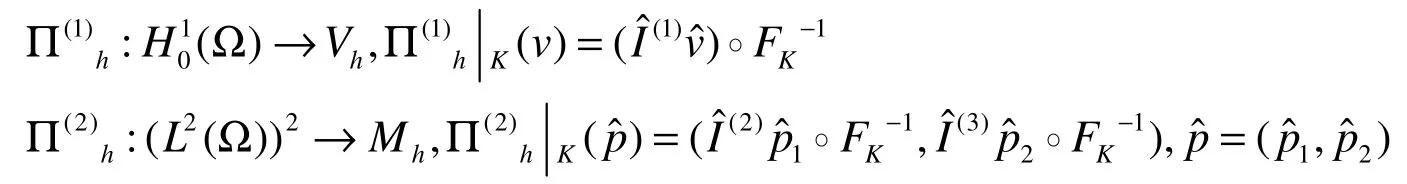
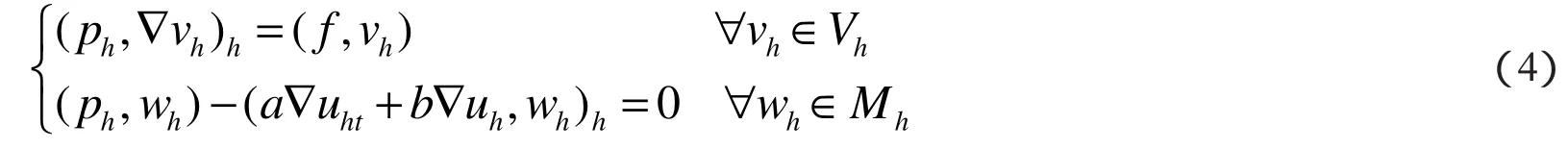
并且逼近问题（4）的解唯一.

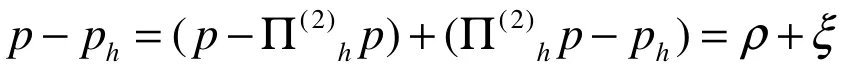
对非协调元来说由式（3）和式（4）可得误差方程

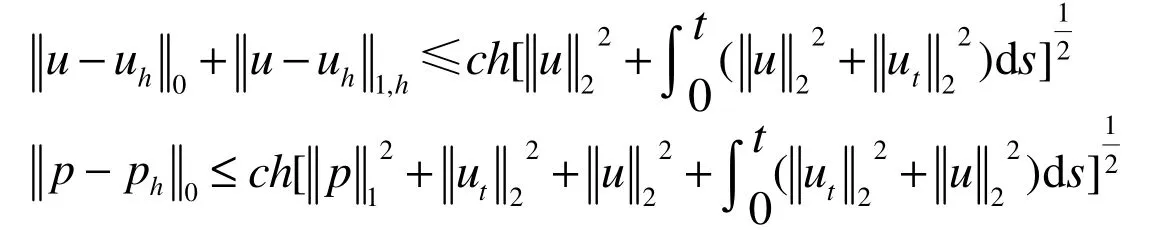
3 超逼近分析

所以有

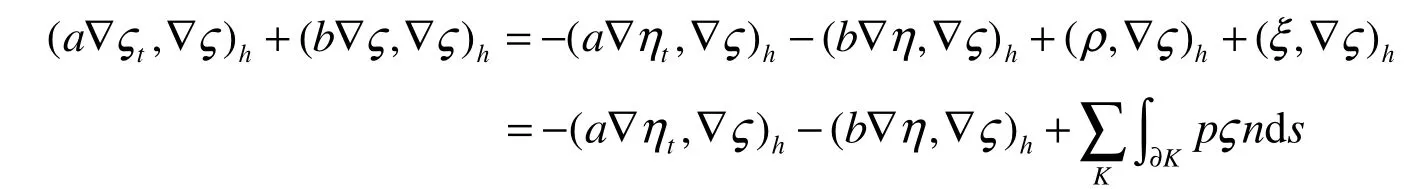
整理得

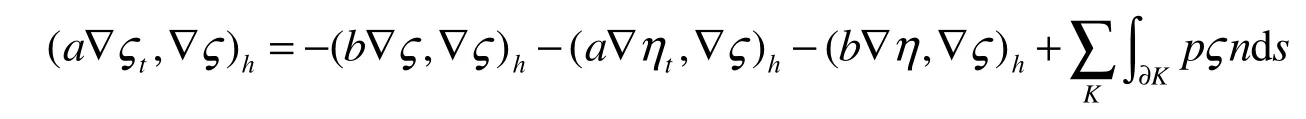
记

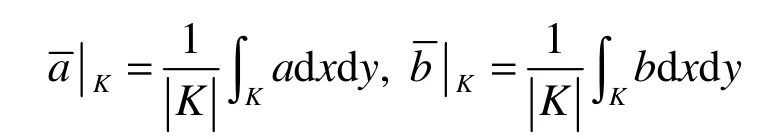
由Vh的构造知

则上式可化为

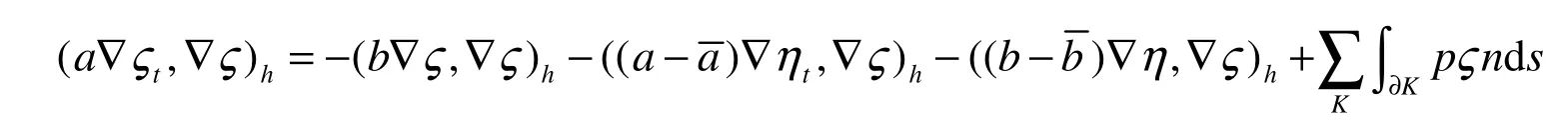
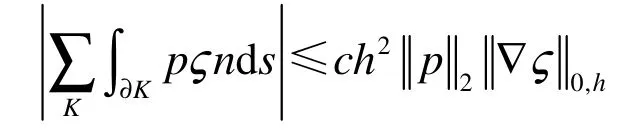
所以有

两边积分得

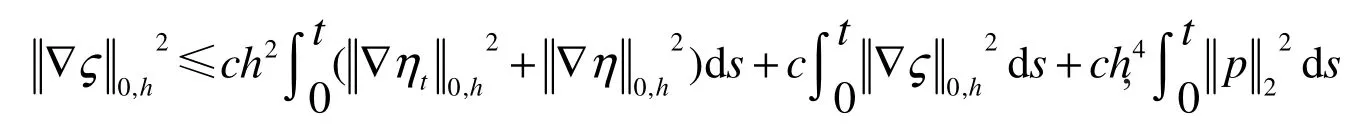
由Gronwall引理得

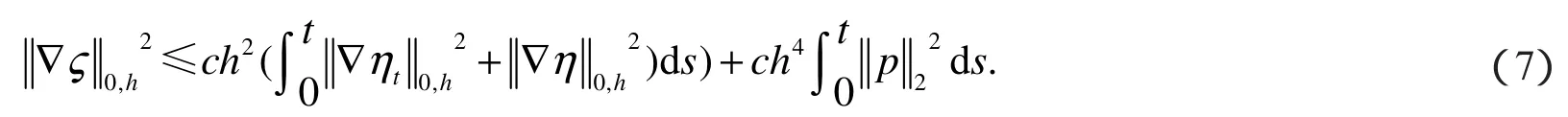
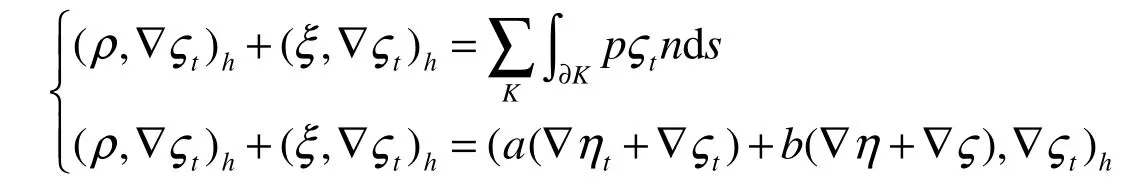
所以有

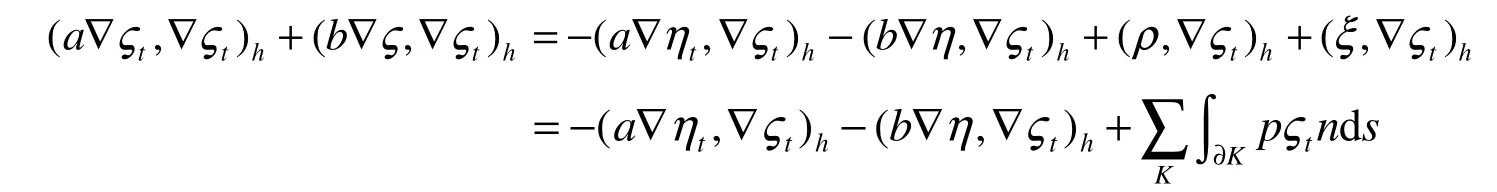
移项得

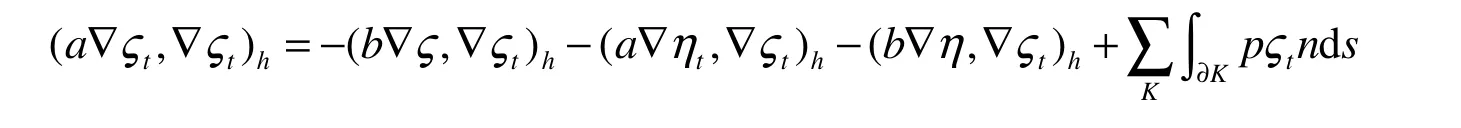
由Cauchy和ε不等式类似（8）有

把式（7）代入式（8）得

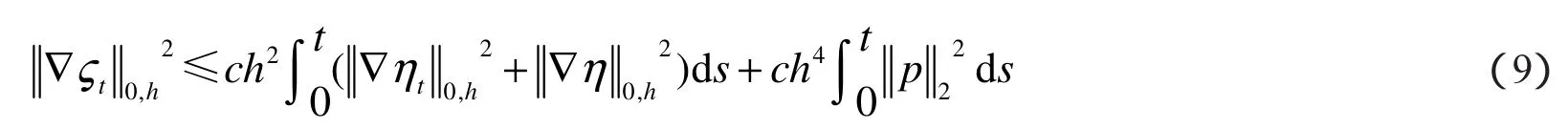
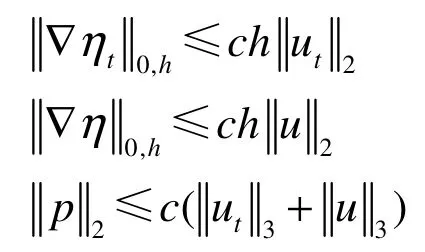
由式（7）和式（9）得

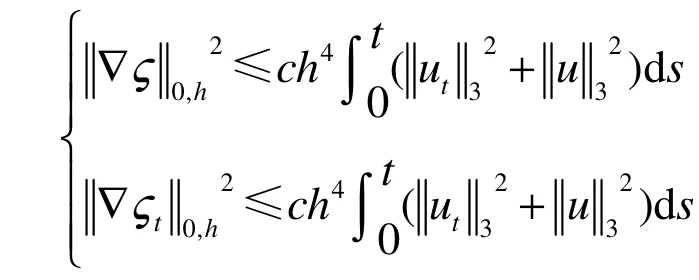
故

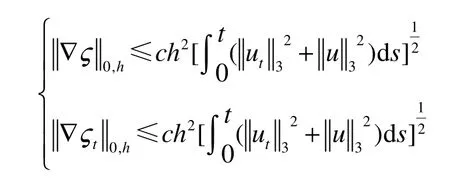
所以

综合上述,估计定理结论成立.

4 结论

本文给出了一个非协调混合有限元格式,在各向异性网格下进行了收敛性分析,对Sobolev方程进行了Galerkin逼近,并且利用单元的特殊性质在不需要Ritz投影情况下得到了超逼近性,最后利用插值后处理技巧给出一类新的混合元格式的收敛性分析和超逼近结果.对求解在流体穿过裂缝岩石的渗透理论,土壤中湿气的迁移,不同介质的热传导等许多物理问题中有广泛应用的Sobolev方程提供了一定思路.

[1]赵培,陈焕贞.Sobolev方程的特征混合有限元法[J].应用数学,2003,16（4）：50-59.

[2]Nakao M T.Error estimates of a Galerkin method for some nonlinear Sobolev equations in one space dimension[J].Numerische Mathematik,1985,47（1）：139-157.

[3]Jiang Z W,Chen H Z.Error estimates for mixed finite element methods for Sobolev equation[J].Northest.Math.,2001,17（3）：301-314.

[4]Gu H M,YangDP.Least-squaresmixed finiteelementmethodsforSobolevequation[J].IndiaJ.Appl.Math.,2003,31（5）：505-517.

[5]郭玲,陈焕珍.Sobolev方程的H1-Galerkin混合有限元方法[J].系统科学与数学,2006（3）：301-314.

[6]郑克龙.Sobolev方程的混合有限元方法[D].成都：四川大学,2005：1-39.

[7]Chen S C,Hai D Y,Zhao Y C.Interpolation and Quasi-Wilson element for narrow Quadrila-teral meshes[J].IMA.J.Numer.Anal.,2004,24：77-95.