改进LS-SVM的直吹式制粉出力软测量建模
冯磊华, 桂卫华, 杨锋
(1.中南大学信息科学与工程学院,湖南 长沙 410083;2.长沙理工大学“可再生能源电力技术”湖南省重点实验室,湖南 长沙,410114;3.湖南江河机电自动化工程有限公司,湖南 长沙 410013)
0 引言
目前,国内外大型火电机组较多采用直吹式制粉系统。由于双进双出钢球磨煤机的煤种适应性强、可靠性高等优点,使其较多的应用于我国南方大部分地区。双进双出钢球磨直吹式制粉系统是大滞后、多变量、强非线性系统,其制粉出力较难直接测量,且很难建立其精确的数学模型[1]。
近年来出现的支持向量机(support vector machine,SVM)是系统回归辨识的强有力工具[2],并且已有基于 SVM的非线性模型预测控制研究[3-5]。标准的支持向量机是一个有约束的二次规划问题,并且约束数目等于样本数量,导致训练消耗时间较长,不利于实现在线控制。为提高SVM的训练效率,Suykens改变了标准SVM的约束条件和风险函数,导出了最小二乘支持向量机(least squares support vector machine,LS - SVM)[6-7]。
LS-SVM的训练只要求解一个线性方程组,使SVM易于实现,并极大地提高了SVM的训练效率。但另一方面,在标准SVM中,只有部分训练数据作为支持向量,具有较好的“稀疏性”;而在LS-SVM中,几乎所有的训练数据作为支持向量,丧失了“稀疏性”[8]。在这种情况下,每一个样本数据都出现在回归模型中,使模型结构复杂,运算量增加。为解决该问题,Suykens率先提出了一种较为有效的LS-SVM稀疏化算法。
在火电厂制粉系统的工业过程中,从生产过程采集的样本数据都存在噪声等多种因素的干扰,在经过数据预处理后难免还有些样本不符合建模要求,这些坏样本对模型的影响很大。因此,本文在Suykens的LS-SVM稀疏算法基础上提出了一种新的改进方式,并将其应用在火电厂双进双出钢球磨制粉出力软测量建模中。
1 最小二乘支持向量机原理及其改进
1.1 LS-SVM原理
设训练样本集{(xi,yi)|i=1,2,…,l},xi∈RN是第i个样本的输入模式,yi∈R是对应于第i个样本的期望输出,l为训练样本数。利用高维特征空间的线性函数
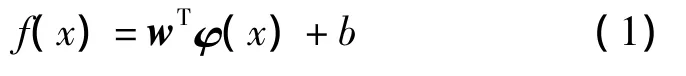
来拟合样本,非线性映射φ(x)将输入数据映射到高维特征空间。LS-SVM回归可以表示为约束优化问题[9-10]为

式中:权向量w∈RNC;误差变量ei∈R;b为偏差量;γ为正规化参数。为求解上式的优化问题,定义其拉格朗日函数为

式中拉格朗日乘子 αi∈R,i=1,2,…,l。根据 KKT条件最终可求得LS-SVM回归模型为

式(4)中核函数项数较多,用其进行泛化时计算量较大,缺乏稀疏性。
1.2 LS-SVM算法的改进
由于火电厂各种干扰因素众多,从而导致从现场采集的有些数据误差较大。因此,对于火电厂制粉系统这一特殊过程,本文在Suykens的LS-SVM稀疏算法基础上进行了如下改进:在删除一些|αi|很小和|αi|过大的训练样本的同时,对于|αi+1|相对于|αi|变化率很大的数据也删除,直到模型性能指标明显下降,这样有助于避免坏样本对LS-SVM模型的影响,简化LS-SVM模型结构。其中,性能指标定义为均方根误差ERMSE,即
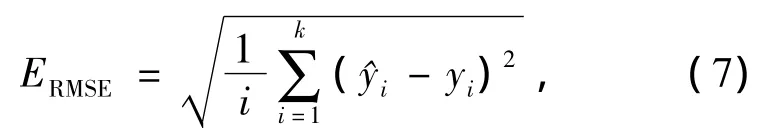
式中:k为预测样本个数,yi为真实值为模型的估计值。
LS-SVM改进的具体步骤如下:
1)将样本数据集分成训练样本和测试样本两组;
2)选择正规化参数和核函数参数,根据训练样本数据训练标准LS-SVM,得到LS-SVM回归模型,计算模型性能指标ERMSE;
3)获取LS-SVM模型的拉格朗日乘子αi;
4)删除一些|αi|过大和|αi|很小的样本数据点及相对于前一点变化率很大的样本数据;
5)剩余的样本数据点作为新的训练样本数据,并转到2),若性能急剧变差(ERMSE急剧增加),算法终止。
2 制粉出力软测量模型的建立
在正常情况下,影响制粉出力的因素较多,主要有:通风量、通风温度、磨内存煤量、煤粉细度、钢球装载量、钢球直径大小及配比、煤的性质、磨煤机长度、筒体直径、磨煤机转速等。具体的影响过程参见文献[11]。
若将以上所有影响因素均作为模型的输入变量,将严重影响学习速度。因此,通过对各因素相对于制粉出力的灰关联排序,选择其中5个因素作为输入参数,分别是:热风门开度、磨煤机电流、磨出口温度、煤粉细度、磨煤机转速[11]。
选取泛化能力较好的径向基核函数:K(xi,x)=,σ为核宽度。
在对制粉出力进行最小二乘支持向量机建模时,有2个参数的选择是非常重要的,即:正规化参数C、核带宽σ。
一般而言,参数C和σ的取值与学习样本和实际问题有关。参数C是在结构风险和样本误差之间做出折衷,参数C的取值与可容忍的误差相关,较大的C允许较小的误差,较小的C则允许较大的误差。核宽度σ与学习样本的输入空间范围或宽度相关,样本输入空间范围越大,σ取值越大,反之,样本输入空间范围小,其取值一般与噪声水平成比例。
基于LS-SVM的模型属黑箱模型,其模型输入/输出之间的非线性函数关系由LS-SVM实现。以各种辅助变量为输入,以制粉出力为输出的预测模型如图1所示。
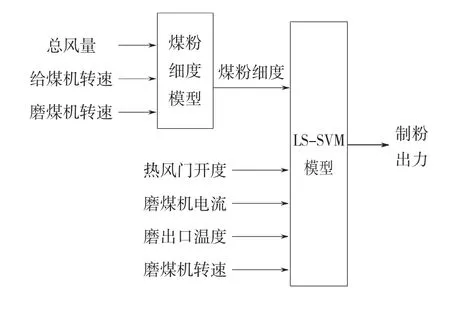
图1 制粉系统出力的LS-SVM模型Fig.1 LS-SVM model of mill output in pulverizing system
在输入层,磨煤机电流用来表示磨内存煤量,有两个测点,分别布置在双进双出钢球磨的两侧,对两值取平均值作为料位信号;煤粉细度较难在线直接测量,但由于其主要跟送风量、给煤量和磨煤机转速有关,因此可将其用关系式表示。模型的输出即为制粉出力,通过预测下一时刻制粉出力的数值进而调整参数,达到预测控制的目的。
3 仿真研究
对某电厂双进双出钢球磨直吹式制粉系统进行连续采样,采样周期为10s。针对LS-SVM算法改进前后分别获得100组实测数据,且数据均经过了归一化处理。将其中50组数据作为训练样本,另50组数据作为测试样本,选择调整参数和径向基核参数分别为C=98、σ=1.2。
分别对改进前后的LS-SVM模型进行仿真,结果如图2所示。
图2(a)为LS-SVM算法改进前,制粉出力的预测值与实测值对比结果;图2(b)为LS-SVM算法改进后,制粉出力的预测值与实测值对比结果。图3为两种模型的仿真结果相对于实测值的误差对比,误差的统计分析结果如表1所示。

图2 LS-SVM算法改进前后仿真结果对比Fig.2 Simulation results comparison before and after LS-SVM algorithm improvement
通过对以上仿真结果分析可得如下结论:
1)采用改进LS-SVM算法建立的软测量模型,学习训练速度较快。图2(a)中,采用标准LSSVM建立的模型,训练时间t=380 s左右时才基本收敛,可以作为预测输出;而图2(b)中,采用改进LS-SVM算法建立的软测量模型,当训练时间t=150 s左右时已经与实测值相差无几,能够表示实际磨煤出力,说明改进 LS-SVM算法的学习速度较快。
2)采用改进LS-SVM算法建立的软测量模型,收敛性更好。采用标准LS-SVM算法建立模型的输出与实测值相差较大,最大绝对误差为20,平均相对误差为0.0760,均方误差为0.0346;而采用改进LS-SVM算法建立模型的输出与实测值相差较小,最大绝对误差仅为9,平均相对误差为0.0231,均方误差为0.0227,均比之前有所降低,收敛性更好。
3)基于改进LS-SVM算法的制粉出力软测量建模,为制粉系统在线学习及优化控制打下了良好的基础。

图3 LS-SVM算法改进前后误差对比结果Fig.3 Error comparison before and after LS-SVM algorithm improvement

表1 预测误差的统计分析结果Table 1 Statistical results of prediction error
4 结语
本文针对火电厂双进双出钢球磨煤机制粉系统这一大滞后、多变量、干扰因素多的特殊工业过程,对标准LS-SVM算法进行改进,在删除一些过大或过小的训练样本的同时,也将变化率过大的数据删除,避免了坏样本对模型的影响,简化了LS-SVM模型。通过采用改进前后的LS-SVM算法分别对制粉软测量模型的仿真结果对比分析可知,改进后的LS-SVM算法学习收敛速度更快,误差更小,改进了标准LS-SVM缺乏“稀疏性”的缺陷,且其泛化性能也有一定提高,更加适用于在线学习,并为制粉系统的在线优化控制打下了良好的基础。
[1]潘维加,邓沙.双进双出球磨机料位控制系统[J].电站系统工程,2009,25(6):61-62.PAN Weijia,DENG Sha.Coal level control system of double-in and double-out ball mill[J].Power System Engineering,2009,25(6):61-62.
[2]VAPNIK V.The Nature of Statistical Learning Theory[M].New York:Springer,1995:38 -76.
[3]KAMBHAMPATI C,MASON J D,WARWICK K.A stable onestep-ahead predictive control of non-linear systems[J].Automatica,2000,36(4):485 -495.
[4]YANG Chihchieh,SHIEH Mengdar.A support vector regression based prediction model of affective responses for product form design[J].Computers & Industrial Engineering,2010,59(4):682-689.
[5]LI Lijuan,SU Hongye,CHU Jian.Generalized predictive control with online least squares support vector machines[J].Acta Automatica Sinica,2007,33(11):1182 -1188.
[6]SUYKENS J A K,VANDEWALLE J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[7]SUYKENS J A K,LUKA L,VAN DOOREN P,et al.Least square support vector machine classifiers:a large scale algorithm[C]//Proceedings of the European Conference on Circuit Theory and Design,August 29 - September 2,1999,Stresa,Italy.1999:839-842.
[8]周欣然,腾召胜,易钊.构造稀疏最小二乘支持向量机的快速剪枝算法[J].电机与控制学报,2009,13(4):626 -630.ZHOU Xinran,TENG Zhaosheng,YI Zhao.Fast pruning zlgorithm for designing sparse least squares support vector machine[J].Electric Machines and Control,2009,13(4):626 -630.
[9]WANG Hu,LI Enying,LI Guangyao.The least square support vector regression coupled with parallel sampling scheme metamodeling technique and application in sheet forming optimization[J].Materials and Design,2009,30(5):1468 -1479.
[10]LI Yankun,SHAO Xueguang,CAI Wensheng.A consensus least squares support vector regression(LS-SVR)for analysis of near-infrared spectra of plant samples[J].Talanta,2007,72(1):217-222.
[11]冯磊华,桂卫华,杨锋.基于一种改进灰关联分析的双进双出钢球磨制粉出力软测量建模[J].仪器仪表学报,2010,31(9):2062-2067.FENG Leihua,GUI Weihua,YANG Feng.Soft sensor modeling for mill output of duplex inlet&outlet ball pulverizer system based on an improved grey relational analysis[J].Chinese Journal of Scientific Instrument,2010,31(9):2062 -2067.

