集值信息系统中基于证据理论的规则提取
田 冉,王国胤,陶春梅
(重庆邮电大学计算机科学技术学院,重庆 400065)
0 引言
证据理论又称为D-S(Dempster-Shafer)理论[1],最初由Dempster在1967年提出,后经Shafer在1976年加以扩充和推广。证据理论是信息融合技术中一种有效的不确定性推理方法,它将概率论中的单点赋值扩展为集合赋值,因此可以看作一种广义概率论。证据理论和传统的概率论相比,能更好地把握问题的未知性和不确定性。证据理论通过对不同的证据进行合成,从而要比仅通过单一证据进行判定的准确性更高。但是证据理论本身也存在了很多问题,比如证据冲突、证据理论的积化性、敏感性等。
粗糙集(rough set)理论[2]是由 Pawlak教授于1982年提出的一种能够定量分析处理不精确、不一致、不完整信息与知识的数学工具,与证据理论存在相似性和互补性,目前关于证据理论和粗糙集之间的关系已经有很多研究[3-4]。经典的粗糙集理论最初主要用于对完备数据集的研究,然而随着近年来的不断发展,粗糙集已经扩展到对不完备数据集的研究。张文修等[5]提出了集值信息系统的概念,并对经典粗糙集理论做了进一步的完善和扩充。集值信息系统与传统意义上的信息系统主要差别在于,其属性值由取单个元素扩展到多个元素的集合,即“集值”[5-8]。
决策规则在很多应用领域都有重要意义,尤其在决策辅助支持领域,能否正确地提取决策规则就显得尤为重要。因此我们可以利用粗糙集理论进行条件属性约简,进而得到决策规则。对于不完备的信息系统,Kryszkiewicz[9-10]定义了容差关系,提出了广义决策和相对约简的概念,并使用不可分辨函数与布尔推理方法得到了每个对象的相对约简和优化决策规则;官礼合[11]则在王国胤教授等人提出的限制容差关系的基础上进一步提出了限制容差关系的改进方法;Leung和Li[12]使用极大一致块方法给出了相对约简的计算方法;Yan和Hong[13]则基于容差关系和极大一致块方法讨论了集值信息系统上的规则知识获取和属性约简;Yu等[14]通过条件信息熵讨论了粗糙集的属性约简;Wu和Mi[15]在相似关系上讨论了证据理论在不完备信息系统中的属性约简。本文中我们主要是将证据理论应用到集值信息系统中,提出了一种基于证据理论的广义决策规则提取方法,和传统的广义辨识矩阵来获取广义决策规则的方法相比,可以更为简单有效地提取最优广义决策规则,并且获得的规则集更小,且降低了在集值信息系统中提取规则的时间复杂度。
1 证据理论
D-S理论是经典概率论的一种推广,它把命题的不确定性问题转化为集合的不确定问题,其中的辨识框架 θ={θ1,θ2,θ3,…,θn}表示一个问题可能答案的论域集合,在θ内的元素间是互不相容的。D-S证据理论基于2θ中进行的元素运算和推理,其中重点是基本概率分配(basic probability assignment,BPA)和信任函数(belief function,Bel)及似然函数(plausibility function,Pl)的确定,得出基本概率赋值后进行证据组合。
定义1 对辨识框架θ,若函数m:2θ→[0,1]满足,则称m(A)是A的基本概率赋值,表示对命题A的精确信任程度。
由基本概率分配函数,可定义相应的信任函数Bel。

Bel(A)则表示A的所有子集的可能性度量之和,即表示对命题A的总信任度。
对辨识框架θ上2个独立的证据信息A={Ai}和B={Bj},m1(Ai)和m2(Bj)分别表示各自的基本概率赋值,则其在θ上的组合可以通过Dempster合成规则对其进行组合。

2 集值信息系统
在集值信息系统中,属性值是用集合的形式表述的。根据集合之间的基本关系是“相交”或者“包容”,从而可以用其属性域中的各个集合间的关系来定义论域U上的相应关系。基于这种思想,张文修等[5]在集值信息系统中定义了2种不同的关系:相似关系和优势关系。
定义 4[7]称 (U,A,F)是集值信息系统,若U={x1,x2,…,xn}为对象集,每个xi(1≤i≤n)称为一个对象;A={a1,a2,…,am}为属性集,每个aj(1≤j≤m)称为一个属性为对象属性值映射,其中fl:U→P0(Vl)(1≤l≤m),Vl是属性al的值域,P0(Vl)表示Vl的非空子集全体。
设(U,A,F)是集值信息系统,在任意属性子集B(B⊆A)上定义二元关系,称这个关系为优势关系,并记为优势类。
定义5[6]设(U,A,F)是集值信息系统,对于任意对象子集X⊆U,记
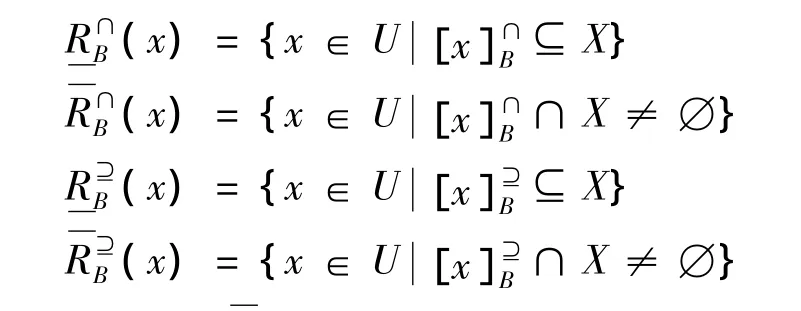
定义 6[6]称 (U,A,F,d)是集值决策信息系统,d为决策属性。有B⊆A,则关于相似关系的广义决策函数定义为;关于优势关系的广义决策函数定义为
如果card(∂B(x))=1,则该集值决策信息系统是协调的,否则称为不协调的。
定义7[6]称B⊆A是集值决策信息系统(U,A,F,d)关于相似关系(或者优势关系)下关于对象 x的广义决策约简,若满足,且对任意)(或者

隐藏在决策信息系统中的命题知识可以表示为决策规则的形式t→s,其中 t=∧(c,v),c∈A,v∈Vc,s=∨(d,w),w∈Vd,t和s分别称为规则的条件部分和决策部分,任何一个集值决策信息系统都可以看做是广义决策规则规则的集合。
3 证据理论在集值决策信息系统上的扩展
定义8[8]由信息系统 (U,A,F)中的一个或者多个属性组成证据理论中的辨识框架θ,属性的值域对应θ中的元素,形式为
定义9[8]对给定的信息系统 (U,A)有规则R(B,C):B1=b1∧B2=b2∧…∧Bi=bi→C1=c1∧C2=c2∧…∧Cj=cj,其中B={B1,B2,…,Bi},C={C1,C2,…,Cj},且B,C⊆A,B∩C= ∅,b1∈,b2∈,..,bi∈,c1∈,…,cj∈。
定义10[8]在给定集合B的属性值的基础上,定义规则R(B,C)的基本概率分配函数为

由此定义规则的信任函数为

规则的似然函数为

则规则的置信区间为[Belr(R(B,C)),Plr(R(B,C))]。
由于本文是在集值决策信息系统上进行讨论,所以下面对属性值和规则的基本概率分配函数在相应的关系上进行扩展。根据定义4中相似类和优势类的定义,有如下扩展定义。
定义11 对于集值信息系统(U,A,F),其中A为条件属性集合,定义Ρ(U)为U的幂集,在Ρ(U)上建立辨识框架m:Ρ(U)→[0,1],对于B⊆A,则定义基本概率分配函数为
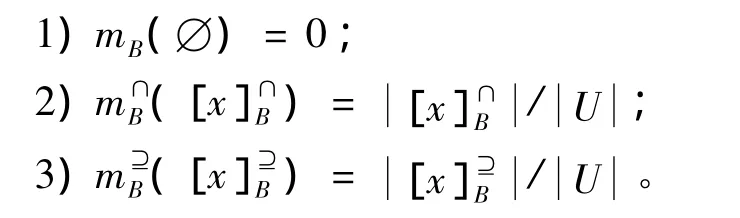
定义12 对于集值决策信息系统 (U,A,F,d),定义 Ρ(U)为 U 的幂集,()为在属性A的相似关系下的广义决策,其中A为条件属性集合,在 Ρ(U)→ ∂上建立辨识框架 m:(Ρ(U)→∂)→[0,1]。
对于B⊆A,则其基本概率分配函数为
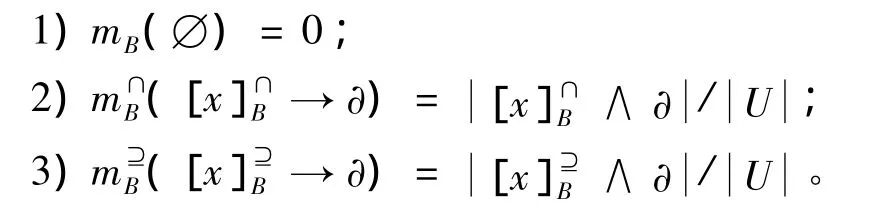
4 集值决策信息系统中的规则提取
利用集值决策信息系统和证据理论的特点,本文提出一种基于证据理论的决策规则提取算法。
第1步:在一个给定的集值决策信息系统中,首先利用文献[15]中的方法,分别在相似关系或者优势关系上进行属性约简。
第2步:如果在相应关系上的属性约简是一个析取式,则把析取式中的每个合取式中的属性分别作为约简属性进行计算,在第4步得出了各自的决策规则后再进行合并。对约简后的每个条件属性建立辨识框架,并求出相应的基本概率分配函数;再对每个属性和相应的广义决策规则建立辨识框架,求出相应规则的基本概率分配函数。根据定义10,如果规则的基本概率分配函数为1,即代表对这条规则的精确信任程度为1,则将这条规则纳入决策规则集。这时得出的规则都为单个条件属性的决策规则。看此时得出的规则能否覆盖整个样本空间,如果能覆盖整个样本空间,则此时的规则集就是我们所需要的决策规则集合。如果不能,则进行第3步。
第3步:从对样本空间覆盖最大的属性值开始算起,即找到拥有最大的m值和次大的m值的条件属性及其属性值。如果2个属性在样本空间上的交集不为空,则进行第4步,否则再次寻找和拥有最大m值的条件属性有交集的条件属性。因为可以覆盖实例最大的属性值相对其他属性值来说最有可能得到决策规则,所以将规则的基本概率分配函数按降序排列后,从最大的开始算起。
第4步:利用第3步得到的条件属性进行两两组合,即对2个属性上建立辨识框架,求出相应的基本概率分配函数。如果结果为1,则把这2个属性及其属性值进行合取作为规则的前件,此时决策规则的后件为相应关系上的广义决策。看这时得出的规则能否覆盖整个样本空间,如果能覆盖整个样本空间,则此时的候选规则集就是我们所需要的规则。如果不能,则返回第3步重复进行直到条件属性两两组合完毕。如果此时仍然不能覆盖整个样本空间,则在3属性组合的基础上继续添加其他条件属性进行证据合成直到可以覆盖整个样本空间为止。
5 实例分析
这里以文献[15]中的不完备信息系统为例(MAX如表1所示),表1中的不完备信息系统可以转化为表2所示的集值信息系统。

表1 不完备信息系统Tab.1 Incomplete information system

表2 集值信息系统Tab.2 Set-valued information system
这里利用文献[13]中的方法进行条件属性约简,可得条件属性约简为 (Price,Size,Max-speed)。
对于约简集合 B1=(Price,Size,Max-speed),由定义4可以得到

由定义6可以求出基于关系R∩B的广义决策函数值,如表3所示。

表3 广义决策函数值∂∩BTab.3 Generalized decision function value
对于属性(Price),建立辨识框架θPrice={high,low},且 [price(x)=high]∩={x1,x3,x4,x5},[price(x)=low]∩={x2,x3,x5,x6},则由定义 11得:(将 [price(x) = high]∩简 写 为high∩)m(high∩)=4/6;m(low∩)=4/6。
对于属性(Size),建立辨识框架 θSize={full,compact},同理得:m(full∩)=5/6;m(compact∩)=1/6。
对于属性(Max-speed),建立辨识框架 θMax-spd={low,high},得:m(low∩)=4/6;m(high∩)=3/6。
将每个条件属性和决策属性相对应,再建立相应的辨识框架。
将条件属性(price)和其对应的广义决策∂建立辨识框架:θprice,∂={(high,low),(good,poor,excel)},则其相应的基本概率分配函数为:m(high∩,good)=1/6;m(high∩,poor)=1/6;m(high∩,good ∨excel)=2/6;m(low∩,good)=1/6;m(low∩,poor)=1/6;m(low∩,good∨excel)=2/6。
将条件属性(size)和对应的决策属性d建立相应的辨识框架:θsize,d={(full,compact),(good,poor,excel)},则其相应的基本概率分配函数为:m(full∩,good)=2/6;m(full∩,good ∨ excel)=3/6;m(compact∩,poor)=1/6 。
将条件属性(Max-Speed)和对应的广义决策∂建立相应的辨识框架:θMax-spd,d={(low,high),(good,poor,excel)},则其相应的基本概率分配函数为:m(low∩,good)=2/6;m(low∩,poor)=1/6;m(low∩,good ∨ excel)=1/6;m(high∩,good∨excel)=3/6。
根据定义10可以求出相应规则的基本概率分配函数,对于规则price→d有:
当price=high∩时:
r1:mr(high∩→ good)=m(high∩,good)/m(high∩)=1/4 。
同理计算可得:

等于1的规则为:r9,r13,它们覆盖的实例分别为{3},{4,5,6}。拥有最大m值的条件属性及其属性值为m(size,full)=5/6,因此从size=full开始和其他条件属性及其属性值进行合成,计算取2个条件属性时规则的基本概率分配函数为

可以得出规则r14,r15,其覆盖的实例分别为{1,2},{4,5,6}。由于 r13已经覆盖{4,5,6},且此时得出的规则已经可以覆盖整个样本空间,因此此时的决策规则为r9,r13,r14。如果未能覆盖整个样本空间,则同理计算其他的组合规则。最终可以得出决策规则为:

且R1,R2,R3均是最优决策规则。
而利用文献[6]中的方法,在相似关系下建立广义决策辨识矩阵:

矩阵中S和X分别代表表1中的属性Size和Max-Speed。
由此得到的决策规则如下。
对象1,2支持的最优决策规则为:R'1:fullSize∧ lowMax-speed→ good 。
对象3支持的最优决策规则为:R'2:compactSize→poor。
对象4,5支持的最优决策规则有2个,分别为:R'3:fullSize→good∨excel和R'4:highMax-speed→good∨excel。
对象6支持的最优决策规则为:R5':fullSize→good∨ excel。
综合以上的决策规则可以可以得出决策规则集为 {R'1,R'2,R'3,R'4}。
本文的方法所求得的广义决策规则和文献[6]中用广义决策辨识矩阵的方法求得的广义决策规则相比,R1,R2,R3和R'2,R'1,R'3相同,都是最优广义决策规则,且没有冗余规则R'4,规则集规模更小,因此可以说明这种提取规则的方法是有效的。从实现方法上来看,本文方法不用对整个决策表建立辨识矩阵,实现起来更为简单方便。从时间复杂度上来看,广义决策辨识矩阵的方法需要对整个决策表建立辨识矩阵,然后从辨识矩阵中提取规则,而本文方法则从单个属性开始计算,直到规则集能覆盖整个样本空间为止,时间上是优于辨识矩阵的,而且就获得规则本身来说,相应关系上的规则可以更好地体现不确定属性之间的关系,且不受缺省值的影响。
同样的,可以求在关系R⊇A下的属性约简为{Price,Milage,Size,Max-speed},求出其决策规则为
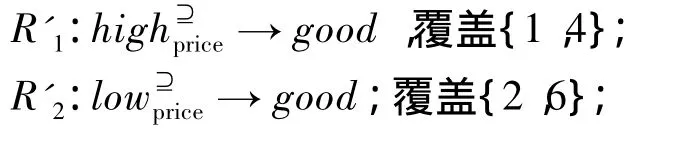

由于在相似关系和优势关系下求出的决策规则是在不同关系下求得的决策规则,计算上并无关联,得到的最优广义决策规则也并无关联[6]。
6 结论
证据理论作为一种处理不确定性信息的有效方法,是当前国内外人工智能领域的热点研究课题,经过多年的讨论研究,其理论和技术都得到了很大的发展。本文提出了基于证据理论的在集值信息系统中的规则提取方法,和传统的规则提取方法相比,有效降低了在集值决策信息系统中的时间复杂度,并用实例说明了这种方法的可行性。
[1]CLENN Shafer.A Mathematical Theory of Evidence[M].Princeton:Princeton University Press,1976:100-248.
[2] 王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001:34-128.
WANGGuo-yin.Rough set theory and knowledge acquisition[M].Xi'an:Xi'an Jiaotong University Press,2001:34-128.
[3]YAO Y,LINGRASP.Interpretations of belief functions in the theory of rough sets[J].Information Sciences,1998,104(1-2):81-106.
[4] WU W,LEUNG Y,ZHANG W.Connections between rough set theory and Dempster-Shafer theory of evidence[J].International Journal of General Systems,2002,31(4):405-430.
[5] 张文修,姚一豫,梁怡.粗糙集与概念格[M].西安:西安交通大学出版社,2006:308-322.
ZHANGWen-xiu,YAO Yi-yu,LIANG Yi.Rough set and concept lattice[M].Xi'an:Xi'an Jiaotong University Press,2006:308-322.
[6]宋笑雪,解争龙,张文修.集值决策信息系统的知识约简与规则提取[J].计算机科学,2007,34(4):182-191.
SONG Xiao-xue,XIE Zheng-long,ZHANG Wen-xiu.Knowledge Reduction and Rule Extraction in Set2valued Decision Information System[J].Computer Science,2007,34(4):182-191.
[7] 张文修,梁怡,吴伟志.信息系统与知识发现[M].北京:科学出版社,2003:78-94.
ZHANG Wen-xiu,LIANG yi,WU Wei-zhi.Information Systems and Knowledge Discovery[M].Beijing:Science Press,2003:78-94.
[8] ANAND S,BELL D,HUGHES J.EDM:a general framework for datamining based on evidence theory[J].Data and Knowledge Engineering,1996,18(3):189-223.
[9]KRYSZKIEWICZM.Rules in incomplete information systems[J].Information Science,1999,113(4):271-292.
[10] KRYSZKIEWICZ M.Rough set approach to incomplete information systems[J].Information Sciences,1998,112(1):39-49.
[11]官礼和.基于粗糙集理论的不完备信息处理方法研究[J].重庆邮电大学学报:自然科学版,2009,21(4):461-466.
GUAN Li-he.Processing incomplete informationmethods based on rough set[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition,2009,21(4):461-466.
[12] LEUNG Y,LI D.Maximal consistent block technique for rule acquisition in incomplete information systems[J].Information Sciences,2003,153(6):85-106.
[13] GUAN Yan-yong,WANG Hong-kai.Set-valued information systems[J].Information Sciences,2006,176(5):2507-2525.
[14] YU Hong,YANG Da-chun,WANG Guo-yin,et al.A Knowledge Reduction Algorithm Based on Conditional Entropy[J].The Journal of China Universities of Posts and Telecommunications,2001,8(3):140-149.
[15] WU Wei-zhi,MI Ju-sheng.Knowledge Reduction in In
complete Information Systems Based on Dempster-Shafer Theory of Evidence[J].Information Sciences,2008,178(5):1355-1371.

