基于粗糙集理论的两类离散化方法研究
张文波
(重庆邮电大学计算机科学与技术研究所,重庆 400065)
0 引言
信息系统连续型属性值的离散化对决策规则或决策树的学习具有非常重要的意义,它能够提高系统对样本的聚类能力,增强系统抗数据噪音的能力,减少机器学习算法的时间和空间开销,提高其学习精度。由于最优离散化问题是NP(non-deterministic polynomial)困难的,因此在实际应用中通常采用启发式算法来计算次最优结果。粗糙集是一种有效的数据离散化工具,基于这一模型已发展了很多典型的启发式离散化方法,但研究结果表明,没有一种绝对好或绝对差的通用的离散化方法[1],因此,需要研究不同离散化算法的特性,以便为不同的数据集选择合适的算法。
大部分现有的基于粗糙集理论的启发式离散化方法都是建立在一种辅助矩阵基础之上[2]。由此我们可以将离散化方法大致分为2类:一类是基于辅助矩阵的算法;另一类算法在离散化过程中则没有建立和利用辅助矩阵。基于信息熵的离散化算法就是后一类算法的典型代表。本文通过系统实验研究,分析比较了基于辅助矩阵和基于信息熵的典型算法的性能。结果表明:基于辅助矩阵的方法性能比较稳定,通用性相对较强,但复杂度较高,较适合于处理小容量数据集;信息熵类算法的识别率虽低于辅助矩阵类算法,但是在正确识别率方面有一定优势且计算时间短,适合于处理较大容量数据集。
1 两类启发式离散化算法思想
粗糙集研究和处理的对象通常是决策系统,记为S=(U,V,f,C∪{d}),其中:U 是有限样本集合,称为论域;C是描述样本的条件属性集合,d是决策属性,C∩{d}= ∅;Va=[la,ra]是属性 a∈C∪{d}的值域,V=∪Va;f:U→C∪{d}是从样本空间向属性空间的映射函数。
样本x∈U在属性a∈(C∪{d})上的取值通常记为a(x),即f(x,a)=a(x)。若S中存在取值连续的属性,则需对S进行离散化。
一般说来,基于粗糙集理论的启发式离散化算法都是以相邻属性值的平均值为候选断点[3],然后根据某种启发式标准,从候选断点集合中选择一个能保证原系统的样本分辨关系、且足够小的子集来对系统进行离散化。不同启发式算法最核心的区别就在于它们采用不同的启发式方式来度量候选断点的重要性。
1.1 基于辅助矩阵的离散化算法
这类算法根据决策系统及其候选断点集合来构造一个辅助矩阵,并通过考察矩阵的特征来计算候选断点的重要性。
定义1 给定S=(U,V,f,C∪{d})及其候选断点集合R*,S*=(U*,R*)是其辅助矩阵,其中:是属性a的第r个候选断点
S*表达了与S相同的样本分辨关系。显然,它能直观地、比较全面地反映候选断点的特征:从列方向看,各列上值为1的元素数目能够直接描述该候选断点对样本的分辨能力;从行方向看,各行上值为1的元素个数反映了能够分辨相应样本对的候选断点的多寡,因而能间接地反映候选断点的重要程度。基于辅助矩阵的各种典型算法就是从不同的角度,按不同的方式来利用S*的行、列方向的特征,计算候选断点的相对重要性,并以之作为选择断点的启发式依据。
1.2 基于信息熵的离散化算法
这类算法通过计算信息熵值来判断断点的重要性,不同的算法对信息熵概念的定义不同。典型的定义断点信息熵的方式有两类。
一类[4-6]是给定属性a∈C上断点q,q将U划分为2个子集(Pj是S中决策值为j的样本的概率分布,r(d)为S的决策种类总数)分别计算E(S1)和E(S2),于是q的熵为
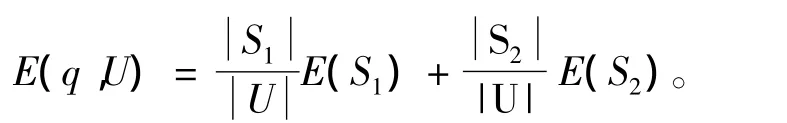
另一类[7-11]方法计算断点信息熵的思路与第一类相似,但不是考虑整个样本空间,而是仅考虑断点两侧属性值区间内的样本分布。这类方法的计算结果通常用于删除最次要的候选断点,合并其两侧的属性值区间。
2 两类离散化算法性能的实验研究
为了分析比较两类离散化方法的性能,我们进行了一系列仿真实验研究,从UCI机器学习数据库①http://www.fmt.vein.hu/softcomp/ucidata/dataset/中选取典型的连续型数据集,测试比较典型离散化算法的性能。实验环境为:Intel(R)Pentium(R)Dual E2180@2.00 GHz 2.00 GHz,960 MB 的内存。实验所用数据集特征如表1和表2所示。

表1 测试数据集的特征Tab.1 Character of Database for test
表1中,No为数据集所对应的序号,Name为数据集的名字,NI为数据集的实例数,NC为数据集的决策属性数。
基于辅助矩阵类算法中我们选择改进的贪心算法 1[12]、列先行后法[13]、行先列后法[13]、改进贪心算法 1 进一步完善算法[14]、二进制矩阵变换[15]5 种方法(分别对应M1-M5);基于信息熵类算法中选择断点信息熵[16]、启发式信息熵[5]、区间类信息熵[7]、区间距离信息熵[10]、EADC[9]5 种方法(分别对应E1-E5)。每组数据集采用5折交叉法进行实验,训练样本经不同的离散化算法处理之后,再进行属性约简和值约简,得到分类规则,最后分别用得到的分类规则对测试样本进行测试。其中,属性约简和值约简均采用现成的算法,我们尝试过多种算法组合,均得到了完全相似的结果。表2—6给出了实验结果,其对应的属性约简算法是信息熵属性约简,值约简算法是归纳值约简[17]。
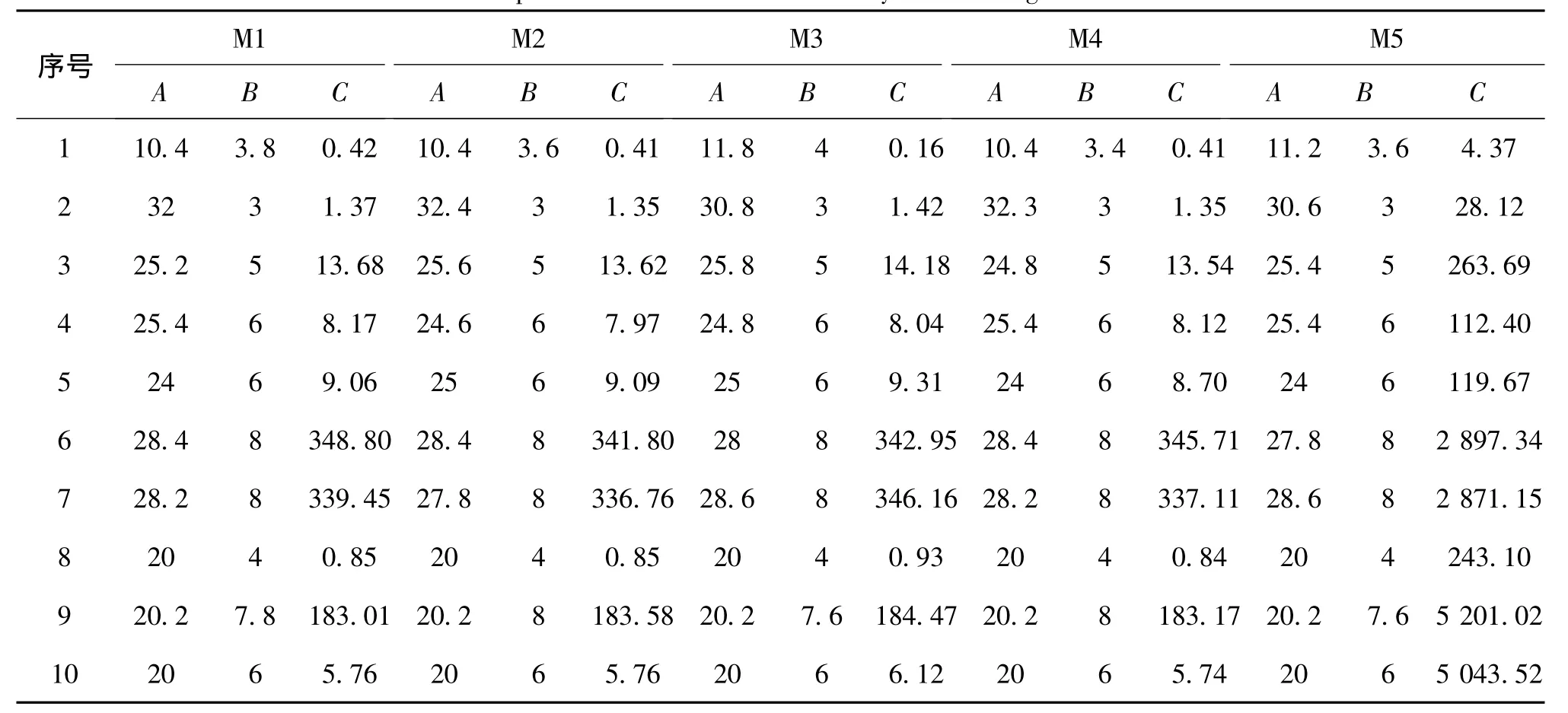
表2 5种基于辅助矩阵的离散化算法结果的简洁性与运行时间比较Tab.2 Concision comparisons of discretized Results by different algorithms of the first kind

表3 5种基于辅助矩阵的离散化算法的识别结果比较Tab.3 Learning accuracy comparison of different algorithms in the first kind

表4 5种基于信息熵的离散化算法结果的简洁性与运行时间比较Tab.4 Concision comparisons of discretized Results by different algorithms of the second kind

表5 5种基于信息熵的离散化算法的识别结果比较Tab.5 Learning accuracy comparison of different algorithms in the second kind
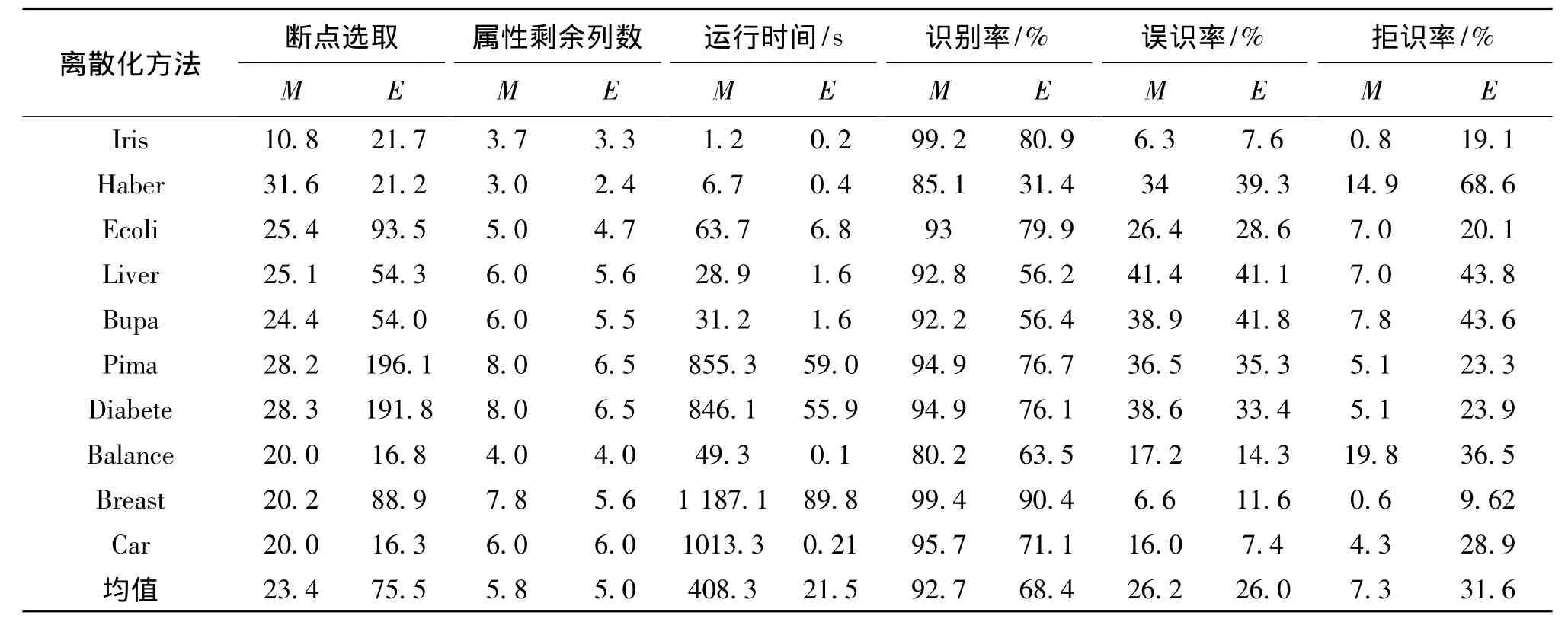
表6 两类离散化算法断点选取个数、属性约简剩余列数、运行时间、识别精度的比较Tab.6 Comparisons of discretized Results by different algorithms of the two classes
2.1 基于辅助矩阵离散化算法结果分析
由表2和表3可以看出,对于同一个数据集:
1)5 种基于辅助矩阵的离散化方法在断点选取、属性约简剩余个数、识别率方面都大致相同;
2)在运行时间方面,前4种算法的运行时间大致相同,而第5种算法的运行时间显著延长。
对一个给定的数据集,这类方法都是依据同一个辅助矩阵来选择断点,只是衡量列和行特征的先后顺序和统计方法不同,相互之间不存在本质性的差异,所以算法的性能大致相当,其中,第5种算法在计算结果断点子集之前,需要先对辅助矩阵进行变换,因而增加了时间开销,使算法运行时间显著延长。
2.2 基于信息熵的离散化算法结果分析
由表4和表5可以看出:即使是对于同一个数据集,5种基于信息熵的离散化方法在断点选取、属性约简剩余个数、运行时间、识别率方面差别都很大。该类方法虽然都是基于一个信息熵的概念,但是衡量标准有很大不同,一类是以计算断点的信息熵为准,一类是以计算区间的信息熵为准(选择阈值),而且计算公式和阈值的选择各异。该类方法与数据的分布有很大关系,比如对于方法E3(或E4),适合一个数据集的阈值在处理另一个数据集时效果往往不好(E4对于数据集8的处理结果)。
2.3 两类离散化算法的比较分析
对基于辅助矩阵类算法中的5种方法结果求平均值,对基于信息熵类的离散化方法结果做相同处理,然后针对所有的数据集求取平均值(见表6最后一列)。由表6可看出:从平均值结果来看,在绝大多数情况下,信息熵类算法所选取的断点要多于辅助矩阵类算法;信息熵类算法能够约简相对较多点的属性,其计算时间要远短于辅助矩阵类算法;依据本实验结果,两类算法相比,辅助矩阵类算法具有更高的样本识别能力,两类算法在正确识别率方面结果大致相同。
为了对结论加以验证,在原有离散化结果的基础上又采用了MIBARK属性约简和一般值约简进行实验,统计实验结果,方法同上(见表7最后一列)。从表7可以看出,实验结果对上述结论得到了很好地支持。
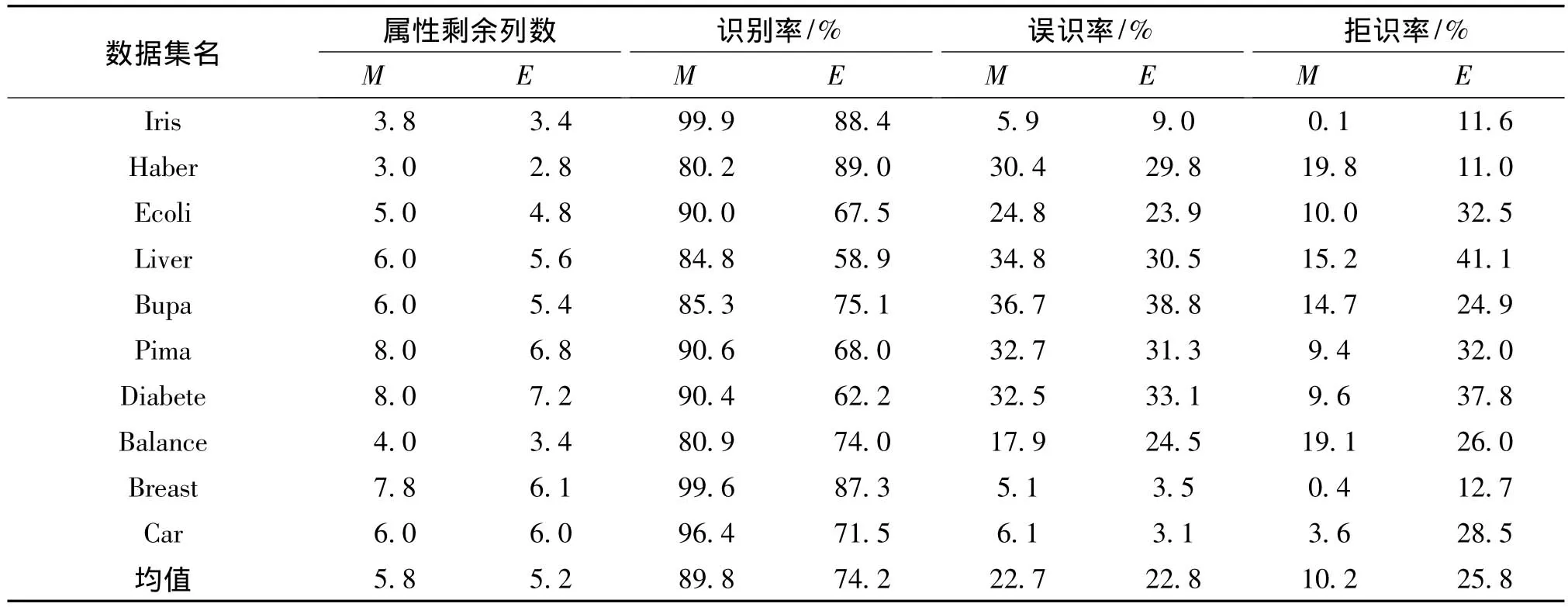
表7 两类离散化算法属性约简剩余列数、运行时间、识别精度的比较Tab.7 Comparisons of discretized Results by different algorithms of the two classes
3 结束语
本文中我们对基于辅助矩阵和基于信息熵的两类离散化方法进行了说明,分析它们的特征且对两类算法中几种比较典型的方法分别进行实验,对实验结果求平均值进行比较。结果表明:辅助矩阵类方法能得到较少的断点、识别率高,但因其空间复杂度和时间复杂度都较大,适合于处理小容量数据集;信息熵类算法的识别率虽低于辅助矩阵类算法,但是在正确识别率方面有一定优势且计算时间短,在样本分布均匀和阈值选择合适的情况下该类方法适合于处理较大容量数据集。所以如何提高信息熵类算法的识别率成为今后有待研究的课题。
[1]PIOTR Blajdo,JERZY W Grzymala-Busse,ZDZISLAW SHippe,et al.A comparison of six approaches to discretiz-ation—A rough set perspective[C]//WANG guoyin,LI Tianrui,JERZY W Grzymala-Busse,et al.RSKT'08 Proceedings of the 3rd international conference on Rough sets and knowledge technology,Beijing:Springer-Verlag,2008:31-38.
[2] FOMINA Marina,KULIKOV Alexey,VAGIN Vadim.The development of the generalization algorithm based on the rough set theory[J].Information Theories & Applications,2006,13(3):255-262.
[3]DAI Jian-hua,LI Yuan-xiang.Study on discretization based on rough set theory[C]//Proceedings of the First International Conference on Machine Learning and Cyberntics,Beijing:[s.n.],2002,1371-1373.
[4]白银柱,裴志利,王建.基于粗集理论和信息熵的属性离散化方法[J].计算机应用研究,2008,25(6):1701-1703.
BAIYin-zhu,PEIZhi-li,WANG Jian.Discreti-zation algorithm ofattributes based on the rough set theory and information entropy[J].Computer application and research,2008,25(6):1701-1703.
[5]李春贵,王萌,原庆能.基于启发式信息熵的粗集数值属性离散化算法[J].广西科学院学报,2007,23(4):235-237.
LIChun-gui,WANG Meng,YUAN Qing-neng.Disc-retization algorithm of attributes based on the rough set theory and heuristic information entropy[J].Guangxi academy of sciences ,2007,23(4):235-237.
[6]沈永红,王发兴.基于信息熵的粗集属性离散化方法及应用[J].计算机工程与应用,2008,44(5):221-224.
SHEN Yong-hong,WANG Fa-xing.Discretization algorithm of attributes based on the rough set theory and information entropy[J].Computer engineering and application,2008,44(5):221-224.
[7]阙夏,胡学钢,张玉红.基于区间类信息熵的连续属性离散化[J].计算机技术与应用进展,2006,236-239.
QUE Xia,HU Xue-gang,ZHANG Yu-hong.Discret-ization algorithm of Continuous attributes based on the rough set theory and interval class information entropy[J].Computer techn-ology and application progress,2006,236-239.
[8]张葛祥,金炜东,胡来招.粗集理论中连续属性的广义离散化[J].控制与决策,2005,20(4):372-376.
ZHANG Ge-xiang,JINWei-dong,HU Lai-zhao.The generalized discretization algorithm of Continuous attributes based on the rough set theory[J].Control and decision,2005,20(4):372-376.
[9]贺跃,郑建军,朱蕾.一种基于熵的连续属性离散化算法[J].计算机应用,2005,25(3):637-639.
HE Yue,ZHENG Jian-jun,ZHU Lei.Discretizat-ion algorithm of Continuous attributees based on entropy.Computer application,2005,25(3):637-639.
[10]徐如燕,鲁汉榕,郭齐胜.基于信息论的连续属性离散化[J].空军雷达学院学报,2001,15(2):20-23.
XU Ru-yan,LUHan-rong,GUOQi-sheng.Discreti-zation algorithm of Continuous attributes based on information theory[J].The air force radars of journals,2001,15(2):20-23.
[11]王国胤,刘静,胡峰.基于断点辨别力的粗糙集离散化算法[J].重庆邮电大学学报:自然科学版,2009,21(3):388-392.
WANG Guo-yin,LIU Jing,HU Feng.Discretiza-tion algorithm of Continuous attributes based on Breakpoint discrimination and rough set theory[J].Cqupt journal,2009,21(3):388-392.
[12]侯利娟,王国胤,聂能,等.粗集理论中的离散化问题[J].计算机科学,2000,27(12):89-94.
HOU Li-juan,WANG Guo-yin,NIE Neng,et al.Discretization question based on rough set theor-y[J].Computer science,2000,27(12):89-94.
[13]赵军,王国胤,吴中福,等.基于粗集理论的数据离散化新算法[J].重庆大学学报,2002,25(3):18-21.
ZHAO Jun,WANG Guo-yin,WU Zhong-fu,et al.New method of data discretization based on rough set theory[J].Chongqing university journal,2002,25(3):18-21.
[14]高赟,侯媛彬.改进贪心算法的完善与应用[J].仪器仪表学报,2004,25(4):727-729.
GAO Bin,HOU Yuan-bin.Perfection and application of improved greedy algorithm[J].Instrumentation journal,2004,25(4):727-729.
[15]侯利娟,颜宏文.基于二进制可辨识矩阵变换的离散化算法[J].计算机工程与设计,2008,29(9):2330-2332.
HOU Li-juan,YAN Hong-wen.Discretization algorithm based on Binary discernibility matrix transformation[J].The computer engineering and design,2008,29(9):2330-2332.
[16]谢宏,程浩忠,牛东晓.基于信息熵的粗集连续属性离散化算法[J].计算机学报,2005,28(9):1570-1574.
XIE Hong,CHENG Hao-zhong,NIU Dong-xiao.Discretization algorithm of Continuous attributes based on the rough set theory and information entropy[J].Computer Journal,2005,28(9):1570-1574.
[17]王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001.
WANG Guo-yin.Rough set theory and Knowledge acquisition[M].Xi'an Jiaotong University Press,2001.
——以大庆长垣萨尔图油田为例

