BP-马尔科夫组合预测方法在光伏发电量预测中的应用

姜侨娜，陈 中

（东南大学 电气工程学院，南京 210096）

传统的日调度计划的制定，主要考虑日负荷预测和传统旋转机组（火力、水力发电等）能力的平衡，并在此基础上进行电力系统优化调度。光伏发电系统的出力抵消了一部分配电网负荷，当发电规模积累到一定数量级后，势必会影响其他传统旋转机组的调度，因此光伏电站日发电量预测对于电网日调度计划有重要的影响。光伏电站日发电量预测的意义在于：①光伏电站的日发电量具有随机波动特点，进行预测可以减少对传统机组的冲击，同时也可以减轻电网对备用的要求；②通过日发电量预测，可以优化新能源与传统能源之间配合，提高电网运行经济性；③合理安排发电容量，充分利用太阳能资源，获得更多的经济效益和社会效益。

光伏电站出力波动性较大，而且目前并网型大规模光伏电站运行时间较短，历史资料和数据都较为有限，因此光伏预测工作具有一定的难度。文献[1]研究基于历史发电量和天气信息的神经网络光伏发电预测，文献[2]、文献[3]对神经网络进行改进光伏预测，文献[4]基于支持向量机算法建立光伏出力预测模型，文献[5]应用人工神经网络多层感知器预测太阳辐射，取得了一定成果，使得基于神经网络模型的光伏发电预测目前有了新的应用。光伏出力预测对历史数据样本要求较高，如果训练样本数据不够充分，训练后的网络结构有时不完全稳定，预测数据通常会在一定范围内随机波动，尤其是面对随机波动较大的情况，其精度会明显降低[6]。

马尔科夫链预测是根据某些变量的现在状态及其变化趋向，预测其在未来某一特定期间内可能出现的状态，适合描述随机波动性较大问题。文献[7]采用加权马尔科夫模型进行负荷预测，得到负荷所属区间，预测精度得到了提高。

本文提出马尔科夫残差对神经网络的预测结果进行修正的方法对光伏电站发电量进行预测，契合光伏发电特点，将二者进行优势互补，从而得到更为准确的预测结论。

1 光伏电站输出功率特性

影响太阳能发电功率的因素很多，例如：太阳辐射强度、阵列的转换效率、安装角度、大气压、温度以及其他一些随机因素。图1为光伏电池的功率电压特性随温度变化曲线图，图2为光伏电池的功率电压特性随太阳辐射变化曲线图。可以看出，光伏电池的输出功率受光伏电池温度T以及太阳辐射强度S的影响。，温度T的增加使得光伏电池的输出功率产生减小的趋势，辐射强度S的增加使得光伏电池的输出功率产生增大的趋势，光伏电池的实际输出功率正是这些趋势相互作用的结果。

图1 功率电压特性随温度变化曲线

图2 功率电压特性随光照变化曲线

对于光伏阵列来说，一个明显的特征就是发电量时间序列本身高度自相关[1]。对于发电量预测模型来说，预测日的发电量是在前一两天的发电量基础上变化的。由于受到天气类型、温度、云层等因素的影响，发电量的变化是一个非平稳的随机过程，但同时又呈现出明显的周期性变化。

2 BP-马尔科夫组合预测模型

2.1 BP神经网络模型

神经网络方法由于实用性强，被广泛应用于各个领域，尤其对具有周期相似性系统预测精度高。光伏发电量的变化呈现出明显的周期性变化特点，契合了神经网络预测的特点。

神经网络模型的精度受到神经网络结构、样本的选取以及数据的预处理方式等诸多因素的影响，在光伏预测建模过程中需对这些细节进一步处理。

预测光伏发电量的拓扑结构，采用典型的3层BP网络，如图3所示。Xi,i=1,2，…，5为输入量（包括历史发电量、日类型、气象因素），Y为输出量。应用BP网络预测光伏发电一般包括4个基本步骤：①收集光伏发电训练和测试样本；②确定光伏预测神经网络结构形式；③进行网络模型训练；④采用训练后的网络完成光伏发电预测应用计算。

图3 BP光伏预测结构

神经元的输出通常被限制在一定的范围，为了消除输入数据因量级相差过大而导致网络不收敛，模型设计好后需要对样本数据进行归一化处理，如公式（1）所示

式中：P为归一化后的光伏样本数据；p为光伏样本数据；pmax、pmin分别为p的最大值和最小值。

光伏阵列发电预测除与历史发电量高度相关外，还与预测日当天的天气情况密切相关，在预测模型中考虑天气信息，会大大提高预测精度。天气预报中给出的天气信息是晴、阴、晴到多云、阴有小雨等模糊日类型描述，为将气象台预测天气的状况应用到光伏发电预测模型中，可采用模糊技术对它们进行模糊化及反模糊化处理[8]。

隐层节点数的选择是建立网络模型的关键，直接影响网络的容量、泛化能力、学习速度和输出性能，隐层节点数与问题的要求、输入输出层节点数的多少都有直接的关系。隐层

式中：m为输出神经元数；a为区间[1,10]内的常数。

输出节点数由预测的内容决定，光伏发电量预测是预测一天的发电总量，该预测量整合至调度系统，得到可行的优化日调度计划。

2.2 马尔科夫链预测模型

光伏电站出力波动性较大，是一个非平稳的随机过程，有限样本训练的BP神经网络结构往往不完全稳定。由于状态概率转移矩阵具有追踪变量随机波动的能力，加之的“无后效性”，因此，与BP模型有机结合，挖掘出发电数据序列的宏观变化与微观波动规律，从而提高模型的预报精度。将神经网络预测值与实际值的相对误差δ所处的不同上下阈值作为状态划分值域。

马尔科夫预测中，最关键的一步是求状态转移概率矩阵。在状态概率的求解过程中，状态的分级显得至关重要，常用的方法有均值-均方差分级法、聚类分析法以及最优分割法。为了简单起见，采用均值-均方差分级法。

根据马尔科夫链理论，考虑一组光伏发电预测误差数据δ，每一试验有多个状态可能发生，若事件Ei发生，则事件处于状态Ei。状态Ei经过k步变为Ej的概率

式中：Nij(k)为样本状态从 Ei到 Ej的转移次数；Ni为状态出现的总次数。则k步状态转移矩阵

利用状态概率转移矩阵，确定光伏预测误差数列中变量所处的状态及其最大概率值maxPij(k)，从而确定变量的下一步转向，然后根据转向概率对光伏预报相对误差值进行修正。

马尔科夫链预测模型可表示为

式中：X(k)为k时刻的状态概率向量；X(0)为初始时刻的状态概率向量；P(k)为状态转移概率矩阵。

2.3 BP-马尔科夫预测模型

预测的基本思想：首先建立光伏发电神经网络预测模型，再对由神经网络预测得到的结果运用模型，分析其误差的波动幅度与波动发展趋势，获得误差的状态转移概率矩阵，并据此矩阵对神经网络预测结果进行修正。

具体步骤如下：

（1）构建光伏发电神经网络，预测样本数据，得出预测相对误差δ;

（2）将测试样本预测值的相对误差δ所处的不同上下阈值作为状态划分值域，建立状态划分标准；

（3）根据残差状态求出状态转移矩阵P(k);

（4）确定初始状态向量X(0);

（5）根据状态转移公式X(k)=X(0)P(k)求出第k步的状态转移结果;

（6）预测值被修正为O=OS（1-δ*）δ*=（δdown+δup）/2，式中：OS为神经网络的预测结果；δdown、δup为所处误差状态区间的上下阈值。

3 BP-马尔科夫预测模型应用

以徐州协鑫光伏发电厂为研究对象建立预测模型，以光伏监控系统数据库2010年10月历史发电数据和气象数据为参考。将数据分组，选择数据的前21组作为神经网络的学习样本，最后将10月31日—11月1日数据组作为检验样本，其它数据作为测试样本。

3.1 建立BP神经网络模型

模型采用预测日及其前一天的日类型、预测日及其前一天的最高气温和预测日前一天的发电量5个输入元素，输出是预测日当天的发电量。

根据公式（2）对隐层节点数进行试算，通过训练次数和总体误差确定最佳的隐层神经元个数。最终建立网络结构为5—10—1，设定学习参数为0.1，学习精度为0.0001，训练次数为1000。

使用构建好的神经网络对测试样本进行预测，通过计算得到δ，结果如表1所示。模型采用均值-均方差分级法将预测的相对误差按照大小分为4种状态：E1[-20%，-10%]，E2[-10%，0]，E3[0,10%]，E4[10%，20%]，建立马尔科夫状态集。

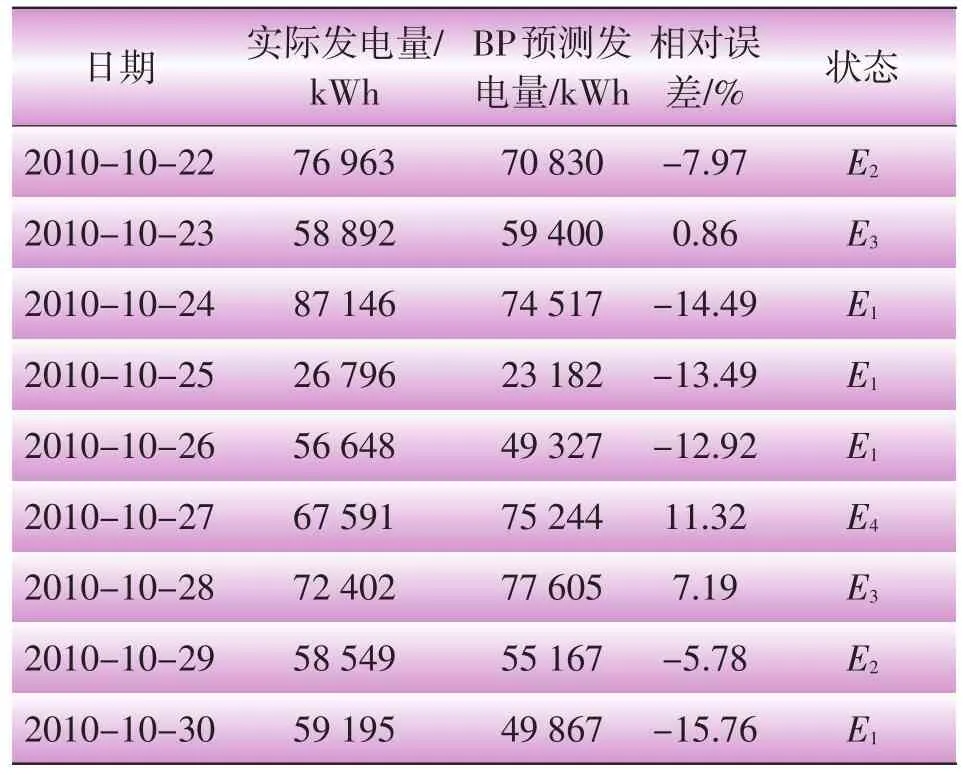
表1 发电量BP拟合结果

3.2 马尔科夫残差修正

根据上述状态区域的划分，可获得BP预测结果状态转移情况，如表2所示。

由表2可确定马尔科夫状态转移概率矩阵

表2 马尔科夫状态转移

应用训练好的BP神经网络对10月22日—10月30日的发电量进行预测，使用马尔科夫方法对其进行修正，结果如表3所示。

经过修正，BP预测的误差有了较大的改善,修正值更接近于实测值。图4为10月22日—10月30日发电量BP预测值和经过马尔科夫修改的预测值。

图4 实际发电量和预测发电量及修正发电量

10月30日所处的状态向量为（1，0，0，0），分别与P（1）、P（2）相乘即得10月31日、11月1日的状态向量（1，0，0，0）、（1，0，0，0），相对误差所处区间都是E1。BP-马尔科夫预测10月31日、11月1日的发电量如表4所示，结果表明经马尔科夫残差修正可以有效的修正神经网络预测值。

表3 马尔科夫修正结果

表4 BP预测结果与马尔科夫修正结果

4 结论

为提高光伏发电预测的精度，本文提出一种以马尔科夫方法进行修正误差的BP神经网络预测模型，模型契合光伏发电功率特点，兼具BP神经模型及模型优点，既能利用较少数据建模，预报总体趋势，又适合于波动性较大的随机序列预报。运用该模型对徐州协鑫光伏电站进行预测，计算结果表明新建模型预报精度高于BP神经网络模型，且该模型简单、计算量小，具有较好的可行性。

［1］陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的设计[J].电工技术学报,2009,24(9)：2-6.

［2］Almonacid F,Rus C,Pérez P J,et al.Estimation of the energy of a PV generator using artificial neural network[J].Renewable Energy,2009,34（12）：2743-2750.

［3］Adnan Sozen,Erol Arcakhoglu,Mehmet Ozalp.Forecasting based on neural network approach of solar potential in Turkey[J].Renewable Energy,2005,30(7)：1075-1090.

［4］粟然,李广敏.基于支持向量机回归的光伏发电出力预测[J].中国电力,2008,41(2)：1-3.

［5］Adel Mellit,Alessandro Massi Pavan.A 24 h forecast of solar irradiance using artificial neural network：Application for performance prediction of a grid-connected PV plant at Trieste,Italy[J].Solar Energy,2010,84(5)807-821.

［6］张树冬,李伟光,南军,等.北方某水库总氮浓度预测的神经网络改进方法[J].计算机技术,2009,35(8)：3-4.

［7］董继征,王桓,何怡刚,等.加权马尔科夫链在负荷预测中的应用[J].继电器,2006,34(3)：1-3.

［8］林星春,曹家枞,陈洁.应用模糊技术的递归小波神经网络太阳日总辐射预测[J].东华大学学报，2007(5)：4-6.