基于非理想维修的状态维修决策模型研究＊

信燕杰 岳冬梅 高 松 张曦霞

（海军大连舰艇学院装备自动化系1） 大连 116018）（海军大连舰艇学院研究生管理大队2） 大连 116018）（武汉军械士官学校3） 武汉 430033）

非理想维修第j个寿命周期可用度的通式为：

1 引言

状态维修的维修决策主要包括最佳维修时机和所应当采用的最佳维修方式。在状态维修中，经常使用的维修方式有大修和中修。中修的优点是维修方便迅速，每次的维修费用低，但是维修效果不理想，同一设备经过多次中修后两次维修之间的运行时间迅速减少，造成装备可用度下降；设备大修的优点是效果理想，达到了修复如新的效果，对下一寿命周期没有影响，但是每次的维修时间较长，不利于装备可用度的提高。

王英［1］依据随机滤波理论和延迟时间的概念建立了以单位时间维修费用最小为优化目标的状态维修决策模型，但维修方式只考虑了设备更新，并不能说明这种维修方式的单位时间平均维修费用最小；胡海军等［2～3］利用比例役龄消减的理论建立了包含非理想维修的延迟时间模型，讨论了不同提高因子下单位时间费用的特性，但是文中的维修时机发生在每次检测到故障时，不符合状态维修只在必要时机对装备维修的准则，造成了维修过剩，以致产生新的缺陷并更快导致故障。

本文根据比例役龄消减（PAR）模型的假设，提出了一种基于非理想维修［4］的状态维修决策优化模型。首先假设对设备进行中修效果是非理想的，对设备进行大修效果是理想的。非理想维修会影响下一个寿命周期两阶段的概率分布及两次维修间的运行时间，进而影响装备的可用度。在此基础上假设对该型设备的维修次数为无穷，建立不同维修方式下装备可用度模型，研究装备可用度随维修提高因子与维修次数的变化规律，对不同寿命周期应采用的维修方式进行优化。

2 非理想维修

在实际维修中，由于维修技术、资源和时间的限制，维修活动并不能理想地修理所有缺陷，大部分维护活动难以使系统真正地修复如新，经过维护后的系统更多地处于一种介于“全新”和“如旧”之间的状态。通常用ρ［5～6］示非理想维修对设备状态的提升程度或改善因子。当ρ＝1时，设备状态达到全新，一般为设备的大修；当0＜ρ＜1时，一般为设备的中修。

3 模型假设与符号

1）假设设备每两次维修间的运行时间称为一个寿命周期，一个寿命周期由正常运行阶段和潜在故障阶段组成。

2）假设一个正常寿命周期的两阶段持续时间分别表示为l1、l2则l1、l2相互独立。

3）假设在离散时刻对被监测设备进行监测，且监测时刻预先确定为T，用tij（i＝1，2，…，n，j＝1，2，…，m）表示第j个寿命周期的第i个监测点，也是当前的状态监测时刻，t0j表示第j个寿命周期的初始时间，令t0j＝0（j＝1，2，…），即每个寿命周期的初始时刻记为0。

4）假设在时刻tij的状态监测信号为yij。

5）假设第j寿命周期的缺陷发生时刻为uj，故障时刻为vj，则有uj＜vj。

其他相关符号的含义如下：

f1（l1）：表示第一个正常寿命周期正常阶段持续时间的概率分布函数；

f2（l2）：表示第一个正常寿命周期潜在故障阶段持续时间的概率分布函数；

p（xij｜Yij）：表示第j个寿命周期各监测点状态关于检测信号的条件概率密度；

p（yij｜xij）：表示第j个寿命周期各监测点检测信号关于潜在状态的条件概率密度；

ζ1，j：表示第j个寿命周期正常阶段的初始役龄，且ζ1，1＝0；

ζ2，j：表示第j个寿命周期潜在故障阶段的初始役龄，且ζ2，1＝0；

Cf：表示对设备进行更新一次的费用：

Cp：表示对设备进行一次非理想修理的平均费用；

Cm：表示对设备进行一次状态监测的平均费用；

Cs：表示设备故障后进行修理造成的经济损失。

4 比例役龄消减模型

PAR模型认为第k次非理想维修并没有使得设备的状态达到全新，假设提高因子［7］为ρ，则相当于状态为全新的ρ倍，也等效为在全新的基础上相当于在该点对设备进行更新的基础上附加了一个初始役龄。根据状态维修具有两阶段性的理论，假设新装备寿命周期的缺陷发生时刻为u，故障时刻为v，则第k个寿命周期正常运行阶段和潜在故障阶段的初始役龄分别为：

4.1 各寿命周期缺陷发生时刻预测模型

假设两阶段的持续时间分别服从威布尔分布，分布函数如下：

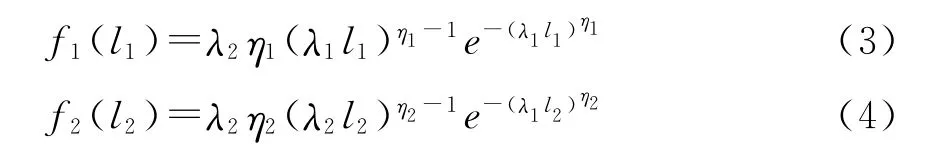
假设经过维修后，新的寿命周期的初始状态重新变为1，且第j个寿命周期初始状态可表示为x0，j，则有p（x0，j＝1）＝1（j＝1，2，…，m）。

各寿命周期内的监测点的状态转移服从马尔科夫过程，则有：

由于缺陷发生时刻在介于正常阶段与潜在故障阶段，所以本文不考虑xij＝3的情况。

每个寿命周期中设备运行过程都具有两阶段性：在阶段1，检测信号随机波动，各寿命周期检测信号独立同分布；在阶段2，检测信号出现异常。第j个寿命周期两阶段检测信号关于所处状态的条件概率分布函数可以表示为：

正常阶段：

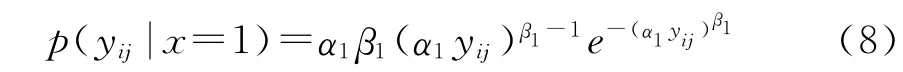
潜在故障阶段：

根据随机滤波理论及贝叶斯公式，各寿命周期内各监测点的状态预测方程如下式：

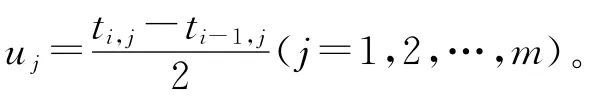
4.2 各寿命周期故障发生点预测模型

［1］利用随机滤波理论来建立新设备在第一个寿命周期内的剩余寿命分布函数如式：

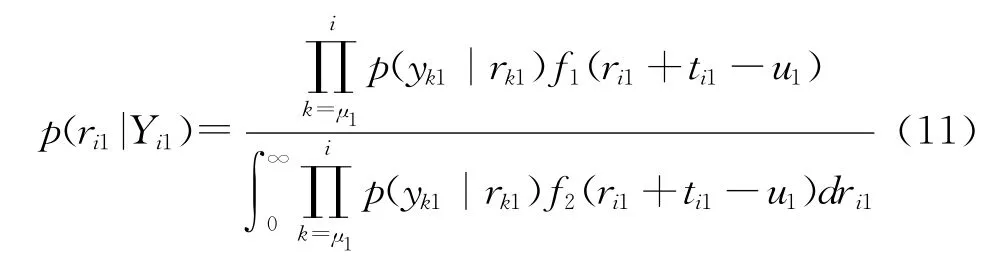
由于第j个寿命周期潜在故障阶段有一个初始役龄ζ2，k＝（1－ρk－1）（v1－u1），所以p（rij＋ζ2，j｜Yij）与P（ri1｜Yi1）独立同分布。即：

式（13）即为非理想维修下的各寿命周期内潜在故障阶段各监测点的剩余寿命预测模型。

各寿命周期潜在故障阶段监测信号关于剩余寿命的条件概率密度函数服从威布尔分布，如式：

5 维修方式的选择

5.1 非理想维修下的可用度［8］模型

非理性状态维修维修费用由每个状态监测点的检测费用和每个寿命周期的修理费用及故障后修理造成的经济损失组成。

假设Tij表示在第j个寿命周期第i个监测点做出的维修时机，则该寿命周期平均停机时间的期望值为：

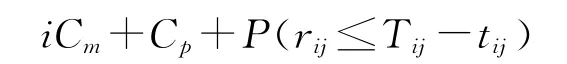
该寿命周期内运行时间的期望值为：

非理想维修第j个寿命周期可用度的通式为：

5.2 理想维修（大修）与非理想维修（中修）的选择

假设理想维修时一个寿命周期的最大可用度为为A，则：在第j个寿命周期内对设备进行非理想维修（中修）的条件为：

在第j个寿命周期内对设备进行理想维修（大修）的条件为：

6 计算机仿真

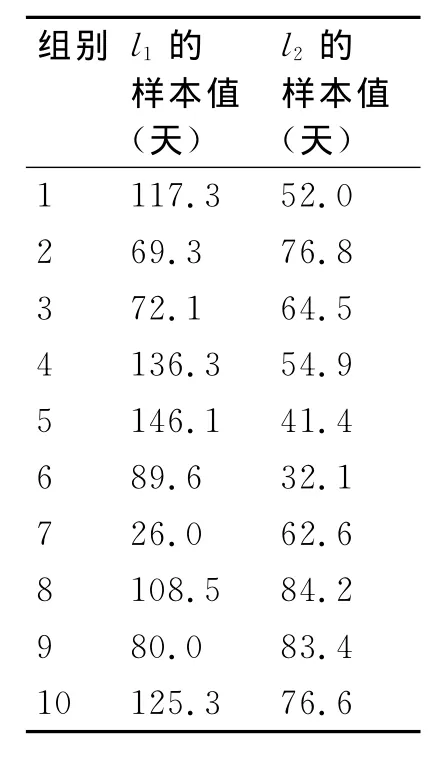
表1 l1、l2 的样本

本实验所涉及的正常寿命周期两阶段的长度样本由数据发生器仿真产生，样本值如表1。

由第一个寿命周期的两阶段持续时间l1与l2的样本值，利用极大似然估计，可以得到l1的l2分布函数的参数λ1＝0.0095，η1＝2.287，λ2＝0.0141，η2＝4。

本实验基于非理想维修对设备进行信息监测，四个寿命周期的监测信息如图1所示。

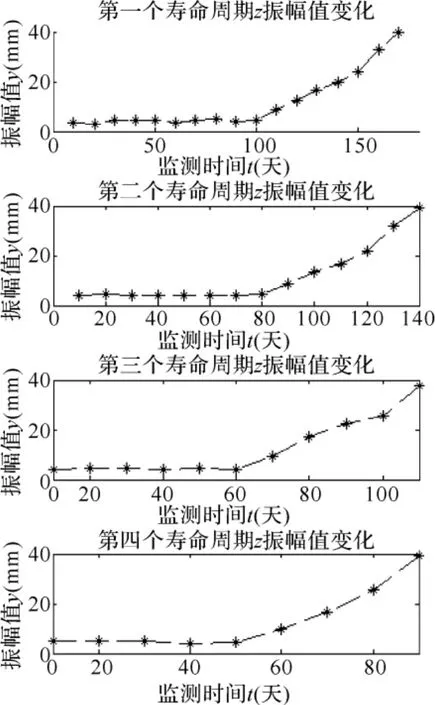
图1 非理想维修下个寿命周期状态检测值

模型中的参数可通过最大然估计得出，假设各参数值如下：

通过计算机仿真，可以维修模型中各寿命周期内缺陷发生时刻及故障时刻，如表2所示。

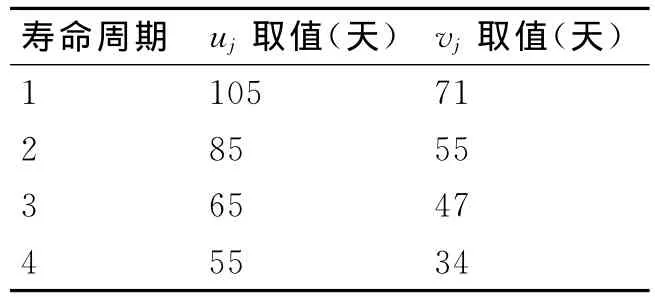
表2 非理想维修各周期缺陷时刻及故障时刻

本文中假设理想维修（大修）、非理想维修（中修）、故障延误时间、一次状态监测的时间分别为（单位：天）：Cf＝60，Cp＝35，Cs＝50，Cm＝0.5。

将时间参数带入式（15），得出理想维修在寿命周期潜在故障阶段各监测间隔期内可靠度随时间的变化曲线，如图1。非理想维修在各寿命周期潜在故障阶段各监测间隔期内可靠度随时间的变化曲线，如图2所示。

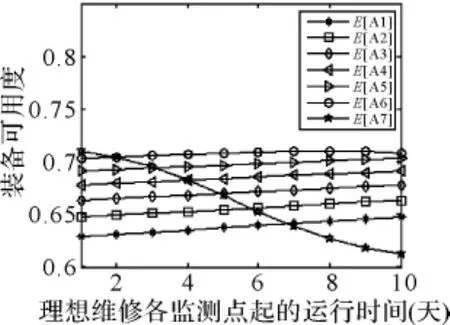
图2 理想维修可用度变化曲线

由图1和图2可知，状态维修在理想维修及非理想维修的四个寿命周期内的最佳维修时机及其所对应的装备可靠度如表3所示。

表3 两种维修方式最佳维修时机及最大可靠度

由图1、图2及表3，可知理想维修的最大可用度A＝71.2%，maxE（A（Ti4））≤A；maxE（A（Tij））≥A，（j＝1，2，3），则一部新装备在不同寿命周期内维修方式的选择方式应按照“中修”—“中修”—“中修”—“大修”的顺序进行排列，才能使该设备在整个运行时间内的可用度达到最大。如图3所示。

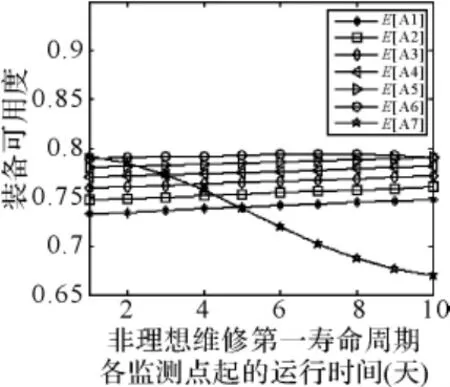
图3（a） 非理想维修第一寿命周期可用度变化曲线

图3（b） 非理想维修第二寿命周期可用度变化曲线

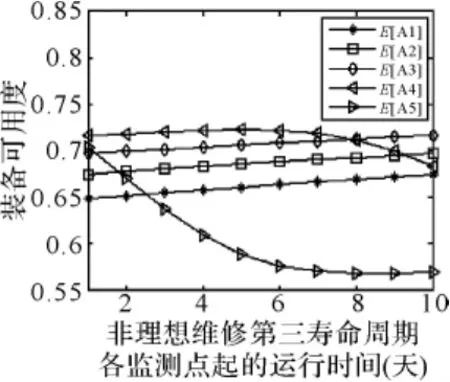
图3（c） 非理想维修第三寿命周期可用度变化曲线

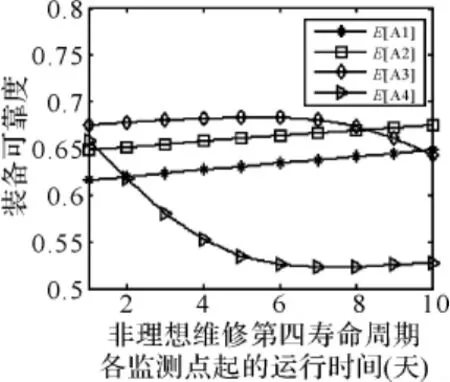
图3（d） 非理想维修第四寿命周期可用度变化曲线

图4 不同寿命周期装备维修方式的选择

7 结语

本文通过建立状态维修的比例役龄消减模型，得出了装备在非理想维修下各寿命周期内的最大可用度，并与理想维修进行比较，发现非理想维修在一定的维修次数内，装备的可用度比理想维修要高，但随着维修次数的增加快速减小。维修次数超过一定的界限后，可用度小于理想维修。因此，在对装备进行维修方式的选择时，将大修与中修有机结合，可得最大的装备可用度。

参考文献

［1］王英.设备状态维修系统结构与决策模型研究［D］.哈尔滨工业大学博士论文，2007（12）：92～109

［2］胡海军，程光旭，段权，等.一种包含非理想维修的延迟时间模型［J］.西安交通大学学报，2009（6），第43卷第6期

［3］SHIN I，LIM T J，LIE C H.Estimating Parameter of intensity function and maintenance effect for repairble unit［J］.Reliability Engineering and System Safty，1996，54（1）：1～10

［4］PHAM H，WANG H.Imperfect maintena-nce［J］.Eropean Journal of Operational Research，1996，94：3425～4385

［5］左洪福，蔡景，王华伟.维修决策理论与方法［M］.北京：航空工业出版社，2008

［6］王禄超，贾希胜，程中华，等.不完全维修策略的产品保修期研究［J］.军械工程学院学报，2010，22（4）

［7］曲玉祥，王剑钊，吴甦，等.基于改善因子的单部件不完全维护优化模型［J］.清华大学学报，2010，50（12）

［8］单志伟.装备综合保障工程［M］.北京：国防工业出版社，2008（10）：154～159