无源双基地脉冲雷达频率同步误差影响分析＊

刘 永 张财生 何 友

（海军驻南京地区航天机电系统军事代表室1） 南京 210006）

（海军航空工程学院信息融合技术研究所2） 烟台 264001）

其中ti表示相参积累时间，上标＊表示取共轭。

1 引言

无源双基地雷达接收系统为了能够利用非合作雷达发射机协同工作，须独立解决在时间、频率和空间上的同步问题［1，3］。而只有保持收、发平台间的频率同步，才能实现对目标回波信号的有效接收和放大。一般情况下，非合作双基地接收系统需要利用其他测频传感器的测量结果或者通过对直达波信号的频率分析结果来调整本振频率。由于直达波信号起伏的影响以及测频传感器精度的限制，难以实现对发射信号频率的准确估计，收、发平台之间总是存在频率同步误差（FSE）。在脉冲多普勒雷达中，对于目前数字中频正交器所能达到的设计精度，一般将忽略其幅相不平衡引入的镜像频率。然而，由于中频正交器的幅相不平衡度是关于频率的函数，在FSE较大时，相对于标称的理论设计值，实际的幅相不平衡度较差，这将导致镜频分量的幅度增大。由于收、发平台之间的频率同步误差，非合作接收机的工作频率可能没有调谐在发射信号的实际载频上，导致多普勒滤波处理之后，静止杂波的频谱不是出现在零多普勒单元上及其附近单元内，目标回波也不是出现在其实际多普勒频率处。而一般无源双基地雷达都是采用广义互相关处理算法来实现目标检测和参数估计［4，7］，此时由于镜像频率分量幅度较大，使得广义互相关处理的输出引入了多个新的干扰频率分量，从而影响模糊平面多个单元的检测和参数估计，因而需要讨论FSE的影响。

本文将从理论上分析无源接收系统的频率同步误差对广义互相关检测算法性能的影响。

2 FSE对PBR中频正交输出的影响

无源双基地雷达接收机（PBR）的主要任务是把截获的射频信号下变频到基带。典型的数字中频正交处理的原理框图如图1所示［8］，输入的中频信号经AD采样后分别与正交本振混频、FIR低通滤波、放大后输出到信号处理机。

图1 中频正交处理原理框图

假设输入基带接收机的数字中频信号为～s（n）cos（（ω＋ω0）n＋φ（n）），其中～s（n）为信号幅度，ω0为信号的中心频率，ω为FSE的大小，即由于对发射信号频率估计不准确而引入的频偏，且ω＜ω0，φ（n）为信号的相位。假设正交处理后I、Q两路输出的信号序列可以表示为

I（n）＝～s（n）cos（ωn＋φ（n））

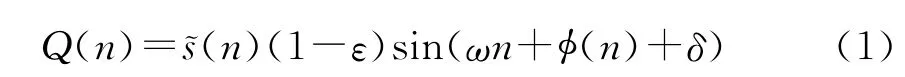
其中ε为I、Q两路间的幅度不平衡度，δ为相位不平衡度。若不考虑频率同步误差和中频正交的幅相不平衡度，则理想的正交处理后的输出序列可表示为

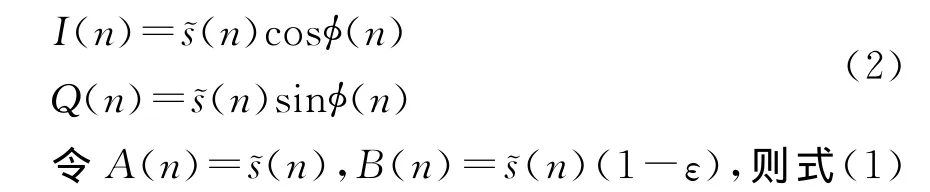
可以表示为

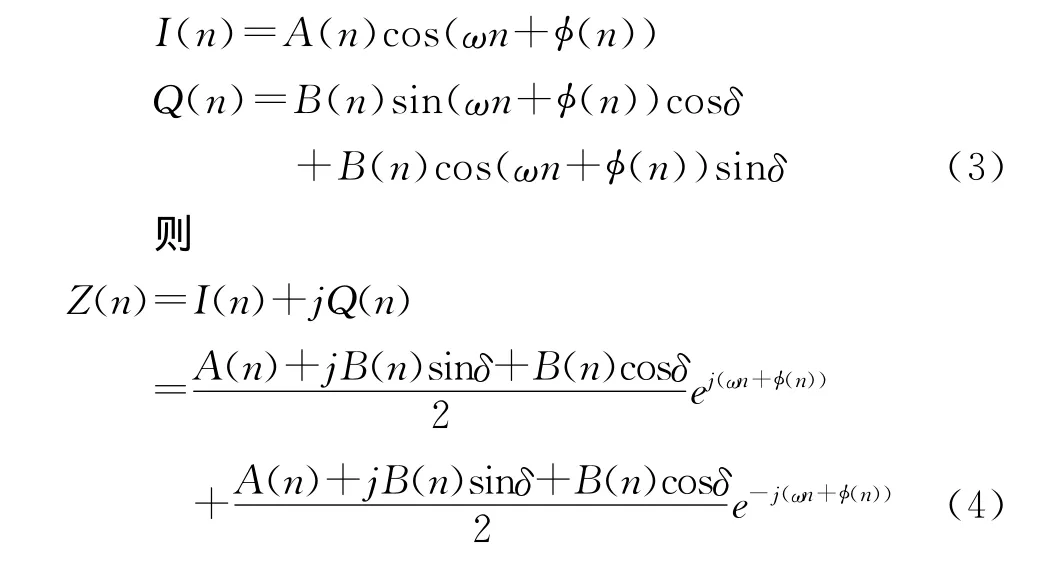
若不考虑频率同步误差和幅相不平衡度，中频正交处理后的输出序列Z（n）可以表示为

则有用信号的功率损耗为

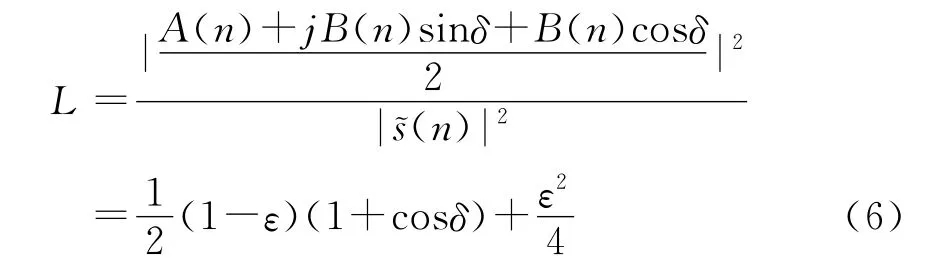
对应地，镜频干扰与有用信号的功率之比为

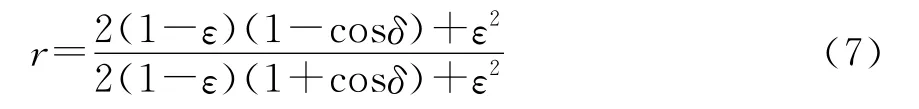
实际上，目前所能达到的设计精度能够使全相参脉冲多普勒雷达接收机的镜频分量的功率比有用信号的功率低35dB～40dB，可以忽略镜频分量引入的功率损耗。

对比式（4）和式（5）可以看出，由于FSE的存在，中频正交处理后的信号频谱并不是出现在零频附近，而是出现在信号剩余载频分量ω及其镜频分量－ω的附近。由式（6）和（7）似乎还可以看出，功率损耗和镜频分量的大小仅与幅相不平衡度有关，与FSE的大小ω无关。然而，由于幅相不平衡度是频率的函数［9］，FSE的增大将使幅相不平衡度恶化，使得镜频幅度增大，功率损耗也增大。

3 FSE对PBR相参检测的影响

一般情况下，无源双基地雷达系统仅能利用在空间同步期间所截获的少数几个脉冲进行相参积累。通过对所截获的直达波和目标回波信号进行互相关处理后，我们希望可以在频域将目标信号与杂波分开，并且能够在强杂波干扰环境下尽最大可能地检测到小目标。事实上，FSE的存在使得静止的杂波的频谱可能不是出现在零多普勒单元上。假使镜频干扰的功率不大，但在对目标回波信号与直达波进行互相关处理后，输出频谱中除了目标回波信号的多普勒频率分量外，还将出现多个其他频率分量。如果系统工作在强杂波干扰区域，则互相关输出的最大峰值对应的频率分量可能就是杂波干扰。因此，由于FSE的存在使得互相关输出的频谱出现许多与目标多普勒频率无关的频率分量，导致系统在对应频率单元及其邻近单元的杂波可见度降低［10］。

下面将定性分析与目标多普勒频率无关的频率分量是如何产生的。虽然互相关检测是在中频信号数字采样之后进行，但为了便于表示，下面将利用信号的模拟形式进行推导。

假设直达波接收机输出的参考信号～XT（t）可以表示为

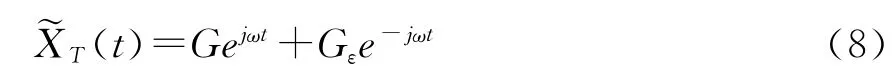
其中ω为FSE引入的剩余载频，对应的幅度为G，Gε为镜频分量－ω的幅度。类似地，假设在相同时刻，系统所监视的空域内只包含一个多普勒频率为ωd的目标，则其回波信号～XR（t）可以表示为

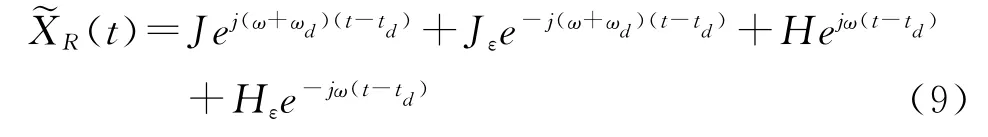
其中ω＋ωd表示目标回波信号对应的实际频率，而杂波分量的频率为ω，td表示双基地路径时延，目标信号幅度为J，Jε为其镜像频率的幅度；H为目标通道静止杂波的幅度，Hε为其镜像频率分量的幅度。

由文献［4～7］可知，无源双基地雷达的目标检测和参数估计的经典方法就是计算基于目标信号与直达波参考信号的距离－多普勒两维互相关函数

其中ti表示相参积累时间，上标＊表示取共轭。

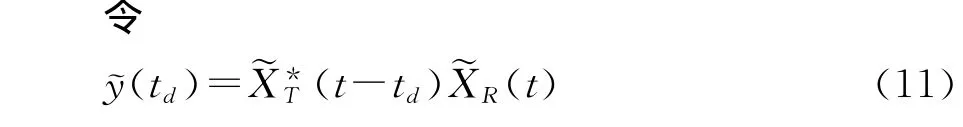
将式（8）和（9）代入式（11），有

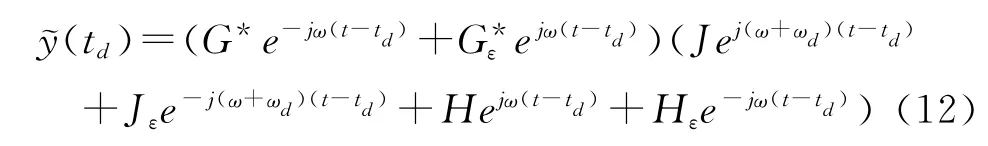
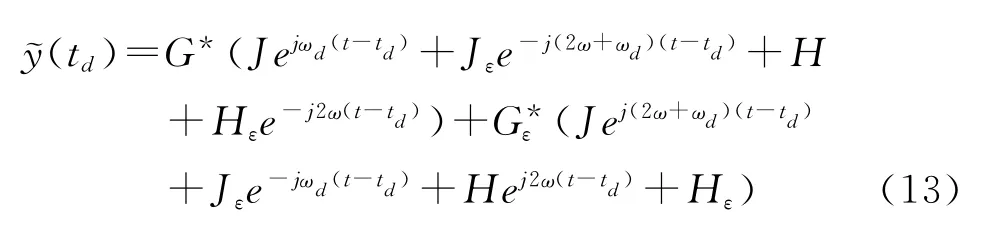
展开式（12），整理可得则在相参积累时间ti内对式（13）进行傅里叶变换，输出频谱含有七个频率分量，而不仅仅是目标所对应的多普勒频率分量ωd，其中一个为互相关处理而产生的零频分量，如图2所示。从图2（c）可以看出，互相关处理后的输出频谱除了目标信号的多普勒频率ωd之外，还有多个其他频率分量。当静止杂波功率很强，且互相关处理仅能利用少数几个脉冲进行积累时，则由此产生的任何一个干扰频率分量都可能导致虚警，甚至掩盖其附近单元的弱小目标。

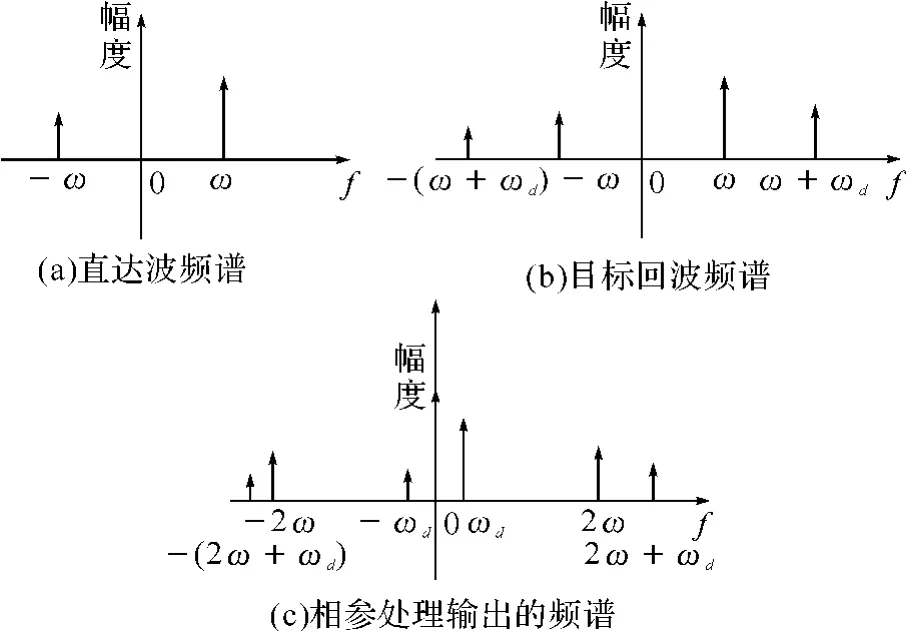
图2 存在FSE时，双基地雷达互相关处理前后对应信号频谱的示意图

4 量化分析与仿真

图3 频率同步时的镜频干扰与有用信号的功率比（dB）

由图3可以看出，在频率准确同步时，相位不平衡度δ为1°时，只要幅度不平衡度ε略小于－12dB，镜频的幅度将比期望信号幅度小30dB，则可以忽略镜频干扰带来的影响。对于一般全相参的主动雷达，其数字中频正交的幅相不平衡度均能够达到该要求，因而可以忽略幅相不平衡度的影响。然而在无源双基地雷达中，由于FSE的影响，幅相不平衡度将变差，导致镜像干扰增大。因此，FSE对无源双基地雷达互相关处理输出引入的误差还需进一步讨论。

为了分析FSE的影响，借鉴文献［11～13］的分析方法，在此我们定义归一化干扰功率（NIP）如下：

rJ＝rH，因此式（14）可以简化为

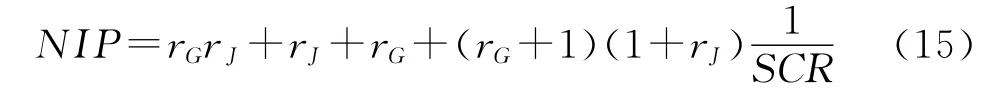
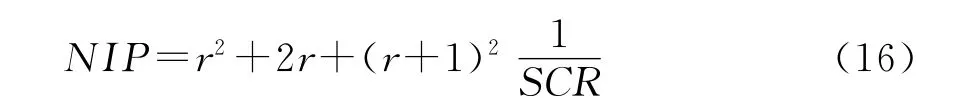
依据式（16），可以给出存在FSE时，目标通道SCR不同时的归一化干扰功率，如图4～图7所示。

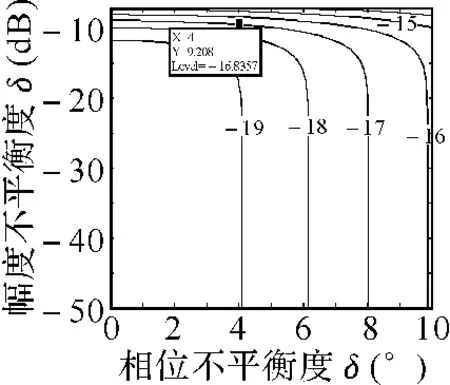
图4 SCR＝20dB时归一化干扰功率的等高线，单位：dB

图5 SCR＝10dB时归一化干扰功率的等高线，单位：dB

图6 SCR＝0dB时归一化干扰功率的等高线，单位：dB

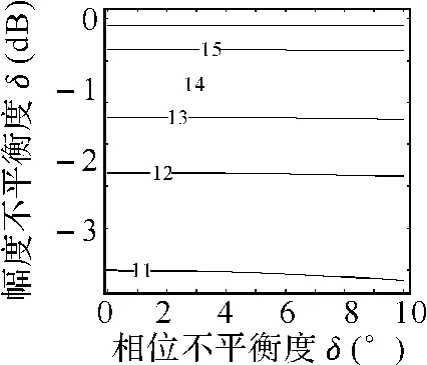
图7 SCR＝－10dB时归一化干扰功率的等高线，单位：dB

当目标通道中SCR分别为20dB和10dB时，互相关处理后输出的归一化干扰功率的等高线与中频正交的幅相不平衡度的关系如图4与图5所示。由图4可以看出，当相位不平衡度小于0.5°，幅度不平衡度小于－15dB时，NIP－20dB，表明接收机中频正交处理器近似理想情况下，杂波干扰的影响将掩盖FSE带来的影响。然而，当由于FSE的影响，系统的相位不平衡度恶化为4°，幅度不平衡度恶化为－9dB时，NIP≈－16dB。而在相同条件下，由图3可以看出，在单基地全相参雷达中对应的镜频干扰比有用信号低约为－25dB，相比较而言，在无源双基地雷达中，此时由FSE引入的误差不能忽略。从图4～图7还可以发现，随着SCR的降低，归一化干扰功率逐渐增大，严重影响动目标检测时的杂波可见度。

事实上，由于FSE的影响，目标信号能量降低的同时还提高了噪声电平，因而NIP还可理解为存在FSE时相对频率精确同步时，相参积累输出SCR的恶化，因此将其作为衡量相参积累输出的运动目标检测性能指标之一是合理的。

5 结语

本文针对无源双基地脉冲雷达系统中，频率同步误差FSE对该系统互相关相参检测的影响进行了详细分析。文章首先给出了接收信号频率没有精确同步时，无源双基地接收系统中频正交处理后输出信号的频谱及其信号功率损耗，定性分析结果表明，由于FSE引入的干扰频率将可能导致无源双基地雷达互相关输出的多个目标检测单元出现虚警，并可能掩盖其临近单元的弱小目标。通过定义归一化干扰功率，定量分析了其与接收系统的幅相不平衡度间的关系，结果表明，系统相参处理输出的多个干扰频率分量将使得目标的杂波可见度减小，严重影响目标信号的检测。

［1］王小馍，匡永胜，陈忠先.监视雷达技术［M］.北京：电子工业出版社，2008：366～369

［2］杨振起，张永顺，骆永军.双多基地雷达系统［M］.北京：国防工业出版社，1998：209～214

［3］W.Q.Wang，C.B.Ding，X.D.Liang.Time and phase synchronization via direct-path signal for bistatic synthetic aperture radar systems［J］.IET Radar Sonar Navigation，2008，2（1）：1～11

［4］宋杰，何友，蔡复青，等.基于非合作雷达辐射源的无源雷达技术综述［J］.系统工程与电子技术，2009（9）：2151～2156，2180

［5］P.E.Howland，D.Maksimiuk，G.Reitsma.FM radio based bistatic radar［J］.IEE Radar，Sonar and Navigation，2005，152（3）：107～115

［6］K.S.Kulpa，Z.Czekała.Masking effect and its removal in PCL radar［J］.IEE Radar，Sonar and Navigation，2005，152（3）：174～178

［7］H.D.Griffiths，C.J.Baker.Passive coherent location radar systems.Part 1performance prediction［J］.IEE Radar，Sonar and Navigation，2005，152（3）：153～159

［8］弋稳.雷达接收机技术［M］.北京：电子工业出版社，2005：106～107

［9］James Tsui.Digital Techniques for wideband receiver［M］.MA：Artech House Inc，2001：254～257

［10］宋杰，何友，关键，等.一种双模杂波抑制的准自适应MTI系统［J］.兵工学报，2009（5）：546～550

［11］Choi Y.S，Voltz P.J，Casara F.A.On channel estimation and detection for multicarrier signals in fast and selective Rayleigh fading channels［J］.IEEE Trans Communication，2001，49（8）：1375～1387

［12］孔永锋，施伟斌.广播式OFDM系统同步方法的设计与仿真［J］.计算机与数字工程，2009，37（11）

［13］束锋，程时昕，李重仪，等.OFDM无线通信系统的时间和频率同步误差分析［J］.中国科学E辑信息科学，2005，35（2）：135～149