多普勒辅助RangeFit快速定位方法

孙金海，汪峰，李金海，阎跃鹏

(中国科学院微电子研究所电子系统总体室，北京100029)

GPS等卫星导航定位系统进行用户位置定位时需要知道卫星的位置和观测的伪距，而卫星位置和伪距都与卫星信号的发射时间有关［1-2］，所以接收机要进行定位必须正确地获取卫星发射时间.用户接收机为获取卫星信号的发射时间，必须完成比特同步(bit synchronization)和帧同步(frame synchronization)，即使有卫星星历也至少需要6 s的时间才能完成帧同步，这严重影响到GPS首次定位时间.Niilo Sirola 提出一种 RangeFit［3］方法，Roland Kaniuth称为 Snapshot［4］，文献［5-6］中提出的定位算法与文献［3-4］基本类似，这些方法都是利用卫星信号发射时间1 ms以下的历元计数计算伪距进行定位(本文称为RangeFit方法)，从而不需要进行比特同步和帧同步即可进行定位解算，使得TTFF可在1 s内完成.但同时RangeFit方法也存在一定的缺陷，即初始时间误差、初始坐标误差和钟差等误差的等效距离和需小于150 km，即使初始位置没有误差，初始时间误差也必须在210 s以内，这种约束条件严重影响了 RangeFit法的应用，故大部分接收机指标(TTFF小于1 s)是指在热启动和AGPS条件下的指标.

1 RangeFit快速定位算法基本原理

RangeFit快速定位算法的基本原理是利用卫星信号发射时间ms以下的值，即码相位的值，进行定位解算，不需要进行比特同步和帧同步，从而缩短定位时间.

第i号卫星RangeFit表达式定义［3］如下:

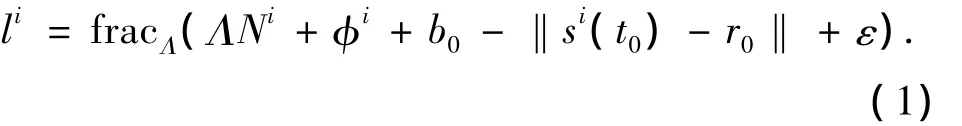
考虑到卫星信号发射时间误差δTs，用于定位的线性化表达式如下:

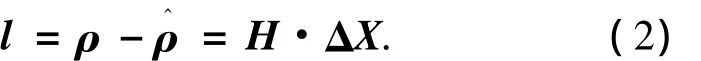
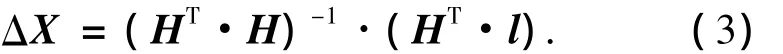
2 多普勒辅助的RangeFit快速定位算法

2.1 RangeFit约束条件分析

RangFit定位的约束条件［3］为

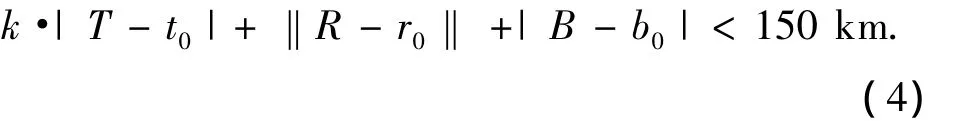
式中:k≈710 m/s;T、R、B为卫星信号发射时间、接收机位置和钟偏的真实值.

从式(1)中可以看出RangeFit方法中钟偏的估计是不完整的，只是估计了1 ms中的一部分;而且从式(1)中可以得出钟偏误差Δb=|B-b0|的大小并不影响RangeFit定位，而是fracΛ(Δb)影响RangeFit定位，故式(3)中的约束条件可以改为:

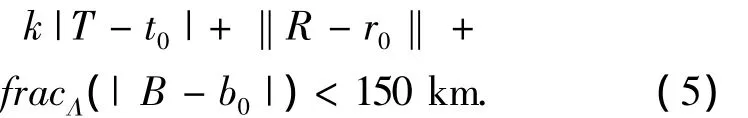
2.2 多普勒辅助

令 F(t，r，b)=k|T-t0|+ ‖ R-r0‖ +fracΛ(|B-b0|)，则 F(t，r，b)＜ 150 km 时，RangeFit方法能够正确进行定位解算.本文采用载波多普勒作为主要观测量进行解算，获得(t，r)更为准确的近似值，使 F(t，r，b)小于 150 km.

将式(2)进行微分得

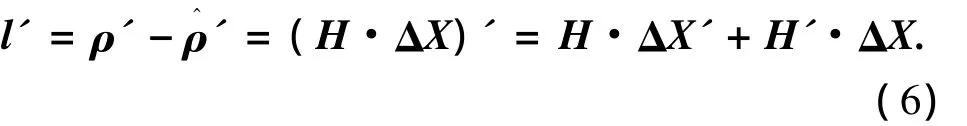
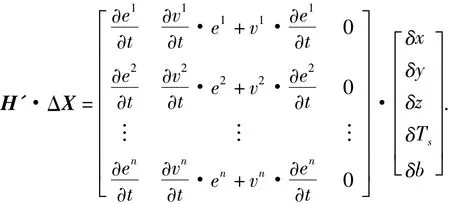
令 δx'=0、δy'=0、δz'=0、δTs'=0、d'=l'，则式(6)可写为

则多普勒辅助解算公式如下:

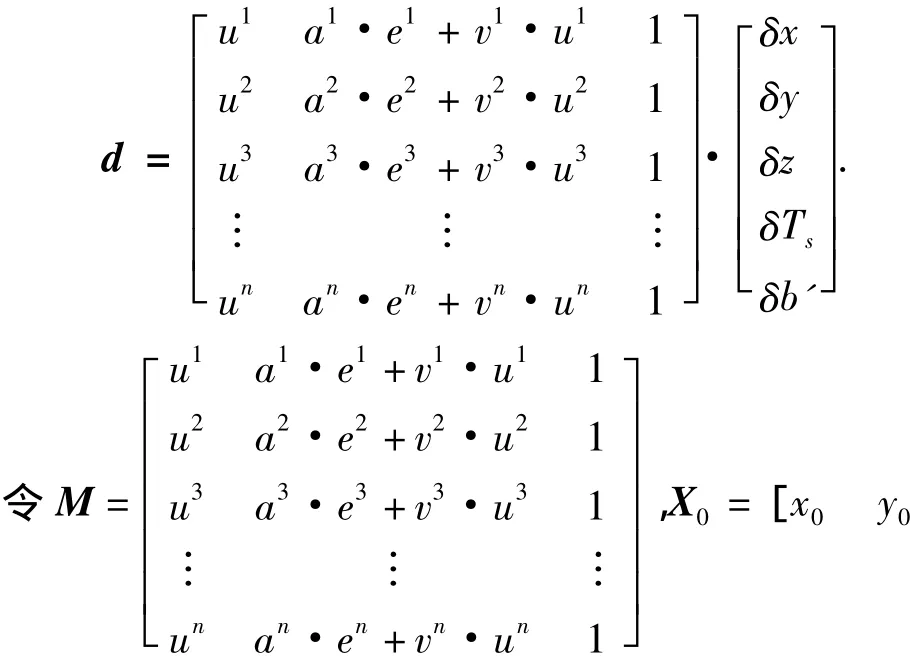
z0t0b0］T为初始状态量，则多普勒辅助解算的值为

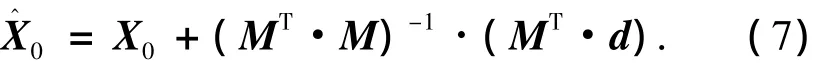
3 多普勒辅助RangeFit算法性能分析

本文对采用实测上述方法进行性能分析，考虑到静态数据易于进行误差仿真分析，而且整个算法流程并不区分动态还是静态环境，所以本文性能分析采用的是静态数据，其坐标经纬度和高度表示为(39.953 854 1°，119.611 263 7°，53.79 m).通过对上述算法的分析和实际数据测试，发现相对于150 km的约束门限，初始坐标r0的偏差并不影响解算的精度，仅仅影响了解算迭代的次数即计算时间，故本文不再对初始坐标r0的偏差做论述，所有分析中采用的初始坐标为r0=(0，0，0).

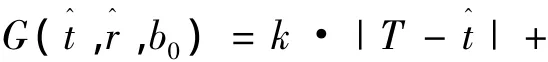
从图1中可以得出在速度误差满足一定精度的情况下，G(x)能够在RangeFit约束门限以内，但是上述方法能够接受的卫星信号发射时间系统误差δTs不能够无穷大，图2为接收机速度误差为Δv=0，解算所能够接受的δTs;下述图中G(x)=0时表示上述方法无法完成解算.从图中可以得出上述方法能够处理的在卫星发射时间系统误差δTs可达到数千秒甚至数万秒，大大突破了RangeFit的约束门限(最大210 s左右)，卫星数越多，能够处理的δTs就越大，在10颗卫星的情况下，δTs在11 000 s(约3 h左右)内都可完成快速定位.

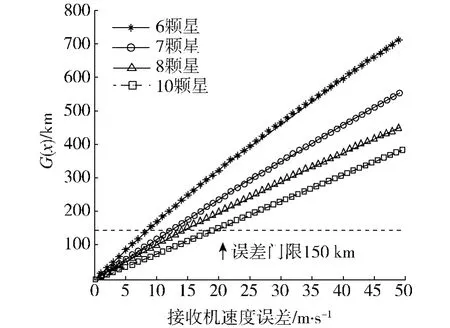
图1 不同卫星数下速度误差与G(x)的关系Fig.1 The correlation between velocity error and G(x)

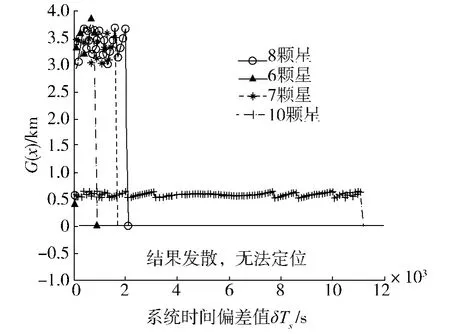
图2 不同卫星数下时间偏差误差与G(x)的关系Fig.2 The correlation between time error and G(x)

4 定位试验

上述方法的定位试验是以本实验室自主知识产权GPS开发平台为基础进行测试的.该平台采用FPGA+ARM9的硬件结构，实时采集实际天空中的卫星信号，并将信号捕获跟踪后的测量结果(EPOCH计数)和解调后的星历信息通过串口输出.本论文中的定位试验是采用C语言平台在实测数据的基础上进行测试的.

本文阐述的算法与动静态测试环境无关，只与初始的速度、时间等误差有关，故为了更好的分析定位结果的误差特性，定位试验采用的是静态环境，其真实坐标为 (39.953 854 1°，119.611 263 7°，53.79).在接收机初始位置未知(解算时设为0)，初始时间误差在1 500 s、并且卫星星历已知的情况下，分别利用常规最小二乘法和多普勒辅助Range-Fit法各进行1 000次开机定位试验，则定位结果如图3和图4所示.从图中可以得出，这2种方法都能够获得令人满意的定位精度，但是多普勒辅助RangeFit的定位结果误差要大于常规最小二乘，主要是因为各卫星的δTs是不同的，而多普勒辅助RangeFit算法做了近似相等处理.

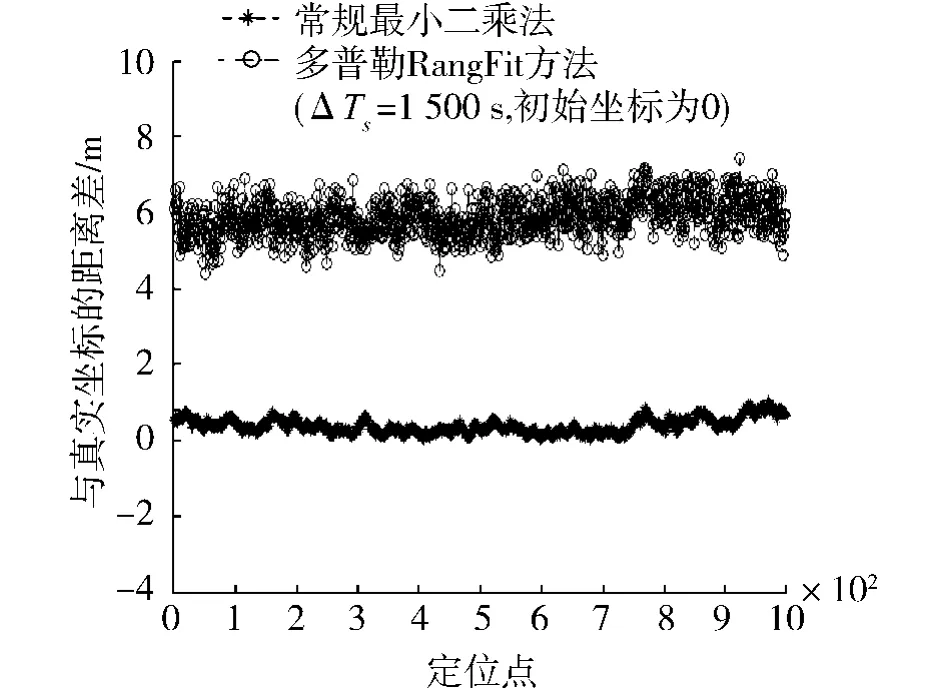
图4 常规最小二乘与多普勒辅助RangeFit定位误差比较Fig.4 Scatter plot of positioning error

对上述两种方法的开机定位时间TTFF进行平均计算得出，采用常规最小二乘法开机平均首次定位时间(TTFF)为6.75 s，而多普勒辅助RangeFit定位法的平均首次定位时间(TTFF)为0.92 s.

5 结束语

本文针对RangeFit方法的约束条件，提出了一种多普勒辅助RangeFit快速定位法，极大突破了RangeFit的约束门限(150 km)，使得TTFF快速定位适用于更多的应用的环境.试验证明，利用本文方法可以在开机时间误差在几千秒甚至几万秒内、位置坐标误差未知的情况下完成TTFF小于1 s的快速定位.该方法不仅可以应用于GPS系统中，而且可以应用在GLONASS、GALILEO和北斗等全球卫星导航系统中.

但该方法还存在一定的缺陷，容易受到初始速度误差的影响，一般情况下首次定时的速度误差需小于54 km/h，虽然能够满足大部分城市环境应用，但对于快速运动载体的TTFF依然存在着一些问题.未来的工作主要集中在进一步完善上述算法模型，同时引入对钟偏误差的消除技术，进一步提高算法适用范围和定位精度.

［1］KAPLAN E.GPS原理与应用［M］.邱致和，王万义，译.北京:电子工程出版社，2001:108-120.

［2］TSUI J B Y.Fundamentals of global positioning system receivers:a software approach［M］.2nd ed.New Jersey:John Wiley＆ Sons Inc，2005:202-209.

［3］SIROLA N，SYRJÄRINNE J.GPS Position can be computed without navigation data［C］//Proc ION GPS 2002，Portland，USA，2002.

［4］KANIUTH R，EISSFELLER B，LEMKE N，et al.A snapshot positioning approach for a high integrated GPS/Galileo chipset［C］//ION ITM 05.Long Beach，USA，2005.

［5］KRASNER N.Method and apparatus for determining time for GPS receivers U.S.:atent 6150，980［P］.1999.

［6］VAN IGGELEN F.Method and apparatus for time-free processing of GPS signals.U.S.:Patent 6 417 801［P］.2000.