快速压缩装置角涡运动特性

刘正先，吴仲义，郑雅芳，罗纪生

(天津大学 机械学院力学系，天津300072)

内燃机快速压缩装置(rapid compression machine，RCM)是一种用于模拟内燃机单循环过程的设备［1-2］.与实体内燃机模型研究相比，具有容易控制实验参数、快速寻求有助于点火的条件、节省能源等一系列优点［2-3］，它能提供实验模拟内燃机内压缩和点火过程的简便方法［4］.因此，快速压缩装置是内燃机研究中极具应用价值的研究工具.

快速压缩装置虽然相对实际装置进行了许多的简化，但仍保持了缸内复杂的流动特征，例如最关键的流动问题之一是与缸内燃烧有关的汽缸壁面与活塞间的角区是否有涡旋流动.Daeyup Lee等［2］研究过RCM中的流动，研究结果表明，在RCM中汽缸壁面和活塞的角区附近存在旋涡，并给出了旋涡的分布特征.但也有一些学者对汽缸壁面和活塞间的角区附近是否有涡表示怀疑.由于汽缸壁面和活塞间的角区是否有涡旋流动对燃烧过程影响很大，因此有必要研究角区附近是否有涡旋流动，其特征是什么，又该如何控制.

计算流体力学(computational fluid dynamics，CFD)通过数值模拟研究流动问题，可以给出流动的细节和各种所需要的流动参数，用以探究复杂的流动过程，解释许多流动现象发生的原因［5-6］，同时也可节省大量的实验耗费和时间.

本文利用CFD数值模拟方法，研究RCM中汽缸壁面与活塞间的角区是否存在涡旋流动，通过涡旋流动参数的分析，达到认识RCM内部涡旋特征，进一步认识内燃机内部复杂流动的目的.

1 数学模型及计算原理

RCM模型示意图如图1(a)，汽缸为固定壁面，活塞的运动速度为U.图1(a)中还给出了Daeyup Lee等［2］分析得出的涡旋分布图:当活塞匀速平动，气体被压缩时，在汽缸壁面和活塞的夹角处会出现涡旋.涡旋分3个区域:涡旋区、剪切区和夹带区.

为了研究RCM实验模型中角区的涡旋，将坐标放在活塞上.在此坐标下，活塞为固定壁，汽缸壁面为运动壁，在非高速的气流运动速度值条件下，这种坐标转换的方法是可行的，不会影响计算结果的准确度［7］;同时可以将由活塞运动形成的动网格变流域转换为定常的固定计算域的流动问题，计算域示意图如图1(b).

图1 RCM实验的计算模型及涡旋的示意图Fig.1 The computational model of RCM and vortex sketch

本文针对Daeyup Lee［2］给出的RCM实验模型，用CFD方法对角区是否出现涡旋，以及涡旋与实验模型几何尺寸的关系进行研究.采用的流动控制方程为雷诺时均方程(Reynolds averaged Navier Stokes，RANS)，RANS 方程的张量形式为

式中:-ρ uiuj称为湍流剪应力或 Reynolds 应力［6］.模化雷诺时均方程中的湍流脉动应力项时采用湍流涡粘模型，即设

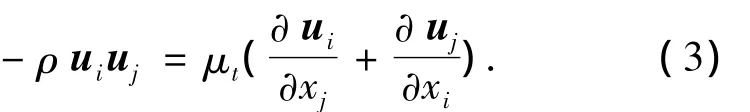
其中，μt为湍流涡粘系数.对湍流涡粘系数的模化采用具有较好普适性的标准k-ε模型.将标准k-ε模型与SA一方程模型、k-ω两方程模型综合比较得到，标准k-ε模型计算更稳定、经济，对网格的适应性更好［9-10］.该模型定义湍流涡粘系数为

其中，湍动能k和湍流耗散率ε满足方程:

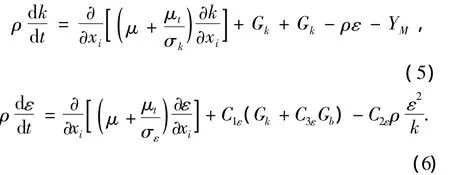
式中:Gk为由于平均速度梯度引起的湍动能产生，Gb为由于浮力影响引起的湍动能产生;YM为可压缩湍流脉动膨胀对总的耗散率的影响.常系数Cμ=0.09，C1ε=1.44，C2ε=1.92，C3ε=0.09.湍流普朗特数分别取 σK=1.0，σε=1.3［6］.

本文采用的工作介质为空气，参照气流运动速度，设定气体不可压缩，参考压力为大气压1.01×105Pa，运动壁面的速度为10 m/s.

2 RCM实验模型计算结果

依照Daeyup Lee等［2］提供的 RCM 尺寸，计算模型为矩形区域，计算尺度为160mm(长，L)×36mm(高，H).根据计算模型和CFD计算软件的设计，本节对不同边界条件下的试验模型进行了计算与比较，以深入了解流场特征.设定计算区域的右壁面为固定壁面边界条件，代表活塞壁面;下壁面为运动壁面.另外，左壁面可变换的边界条件分别为固定壁面和对称面，上壁面的变换边界条件为运动壁和对称壁.所有的运动壁面均向右运动.计算域采用结构化网格，在固壁面处进行网格加密处理，由固壁处向计算域中间渐稀过渡.网格尺度增长率取为1.02，基本网格数300×100.壁面第一层网格尺度为0.1 mm，见图2.计算结果显示，第一层网格满足12.5 ＜y+＜50，符合标准 k-ε 模型的要求.

文献［11-12］研究表明，网格数并非越多精度越高.合理的方法是流动变化剧烈的区域网格加密，流动参数变化不明显的区域网格可以较稀疏，这样既可以保证精度，且计算效率较高.本文通过验算，也得出相同结论.

图2 计算域的网格分布Fig.2 The computational grid

图3 RCM原始尺寸左壁面为固壁的数值模拟结果Fig.3 Numerical simulation result of the original size RCM with wall boundary condition

图3为本文数值模拟得到的RCM实验模型内部流场的速度矢量分布和流函数分布.边界条件如图中所示，上、下壁面向右匀速运动，左壁面为静止固壁面.图中的数值条只表示速度值，而不表示流函数及以后的涡量值，流函数等值线图及涡量等值线图仅用于表明涡的空间位置和方向(下同).从全流场速度矢量图可以看出，在右侧固壁与上、下壁面的夹角区域内产生了涡旋区，涡旋位置与文献［2］一致.从流函数的等值线图可以明显观察到靠近侧壁的一对旋向相反的涡流区.同时还可以发现在RCM实验模型的中心线附近，2个涡的交界处，随着向左延伸，流体出现了摆动的趋势.

图4 RCM原始尺寸左壁面为对称的数值模拟结果Fig.4 Numerical simulation result of the original size RCM with symmetry boundary condition

图4给出了原始尺寸RCM、左壁边界条件由wall改为symmetry的计算结果.结果表明，右壁附近涡旋稳定了，不像图3中有摆动的趋势.从流函数分布也可以看出这一变化.

3 角区涡的形成特征

Daeyup Lee等［2］RCM实验模型研究的结果表明存在角区涡，但由于模型尺度的限制，很难确定涡是在靠近汽缸壁的附近，还是在靠近活塞的中心线附近.为了研究角区涡形成的尺度，分析角区涡的机理，参考Daeyup Lee等［2］提供的RCM尺寸，本节专门研究了角区涡的产生特征.

图5 角涡计算域、边界条件及尺度为160×360的计算结果Fig.5 Computational area for corner eddy，boundary condition and result of RCM 160×360

计算模型的边界条件和网格分布如图5(a)，左壁和上壁边界条件为对称壁，目的是尽量消除这2个壁面对流场的影响.

首先将Daeyup Lee的原始尺寸RCM实验模型在高度方向加长为原来的10倍，即尺度为160 mm(L)×360 mm(H)进行计算.从图5(b)给出的计算结果可以看到，角涡随着高度增加而变大，充满整个流场.在下壁面，流体由运动壁带动，流向活塞壁面，由于活塞壁面的阻挡，流体转向沿活塞壁向上流动，在活塞壁面附近形成了明显的边界层，随着边界层逐渐变厚，流动速度逐渐变慢.受上壁和左壁的约束，流动继续转向，形成了充满整个流场的涡旋，涡心抬升至上半部中心处.

将RCM模型尺度继续扩大为160 mm(L)×720 mm(H)，即高度方向增加为原尺度的20倍，考察涡旋流动的变化.从图6计算结果中可以看出，在运动壁附近仍然存在涡旋，但涡旋在高度方向已不再能充满整个流场了，涡的极限尺度为560 mm左右，其高宽比约为7∶4.

综合分析发现，在左壁面和上壁面均设为对称边界条件下，如果汽缸壁的长度有限，活塞方向的尺度可以很大，那么角区涡在活塞方向存在极限尺度，最大约为汽缸壁长度的3.5倍.显然，这个长度在实际中是存在的.因此，一般情况下，内燃机汽缸中，活塞与缸壁形成的角区中存在角区涡，研究发现，其强度除了与几何尺寸外，还与活塞与缸壁的相对速度有关.

图6 变尺度计算结果Fig.6 The simulation result of geometry scale changed

4 RCM几何尺寸对角区涡的影响

为研究RCM实验模型几何尺寸对角区涡的影响，计算了变长度尺寸下的模型流动.RCM实验模型的长度与高度之比为160/36，约为4.4.

首先，在原始高度下，缩小长度方向的尺寸，计算域为64 mm(L)×36 mm(H)，计算结果如图7.令人意外的是图7中涡的分布并不像图4中那样，出现对称的一对涡旋，而是出现了不对称的一个主涡和周围两个辅涡的现象.此时，L/H=1.78.

其次，又将长度尺度减少为原长的1/5，即32 mm×36 mm，即L/H=0.89进行了计算.图8(a)给出了计算结果，结果显示出涡的分布基本与图7相同，略有不同的是主涡左侧的辅涡消失了，还发现，辅涡可以出现在主涡的上方，也可以出现在主涡的下方，出现的概率是随机的.图8(b)给出了相同边界条件和流动条件下正常收敛解，结果显示辅涡出现在主涡的下方.这表明，RCM装置虽然是对称的，长度尺度相对比较长时，出现的涡在宽度方向是对称的，但随着长度尺度的减小，则会出现其中一个涡的强度和尺度增大成为主涡，另一涡衰减变为辅涡的不对称现象，这种涡的不对称性形成是随机的.

进一步将长度尺度减少为原始长度的1/10，即16 mm ×36 mm，进行计算，长高比为 0.44.结果表明出现的涡又恢复上下对称了，并且很稳定，如图9所示.

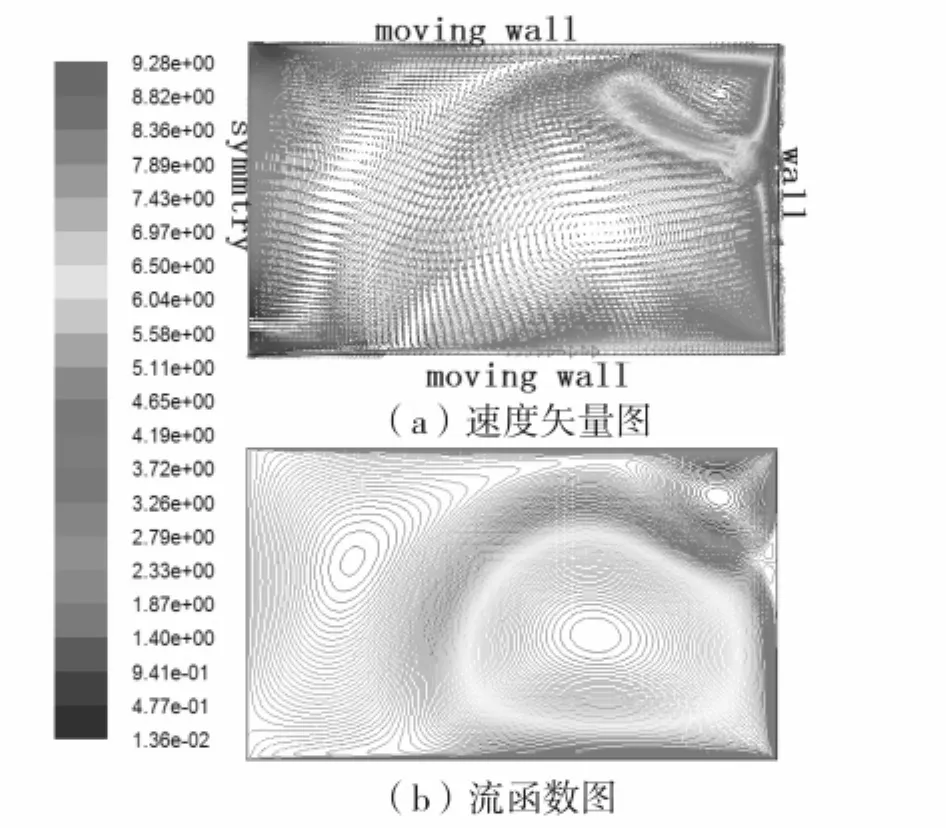
图7 RCM 2/5原长度的模拟结果Fig.7 The simulation result of RCM with two fifith length

图8 RCM 1/5原长度的模拟结果Fig.8 The simulation result of RCM with one fifth length

分析以上数值结果可以发现，模型的长高比例关系的确会对流动结果产生影响.不同的几何关系诱发RCM内部不同的流动主要是角涡现象.根据进一步大量的变长度计算工作分析，可以近似给出矩形RCM的长高比与出现角涡类型的关系:在上、下壁面均为运动边界条件下，矩形RCM的长高比较大时，RCM内部的流动为靠近活塞壁面稳定的一对反向涡旋;当长高比变小，约在0.5～3之间时，RCM内部会出现一个主涡和多个辅涡的情况，而且辅涡的位置和涡形成的过程有关，具有一定的随机性;当长宽比再变小，特别是小于0.5时，流动又呈现与大长高比相同的情况，为活塞壁附近一对反向的涡旋分布.

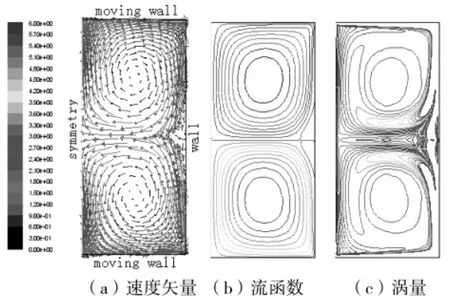
图9 RCM 1/10原长度的模拟结果Fig.9 The simulation result of RCM with one tenth length

5 结论

1)采用CFD方法模拟了内燃机汽缸模型RCM内的涡旋特性，给出了RCM流场中的主要涡旋流动现象.

2)对于典型尺度的RCM，在汽缸和活塞形成的角区附近存在一对反向旋转的涡旋，涡旋充满整个活塞壁.

3)在汽缸和活塞角区附近形成的涡旋的尺度与汽缸壁的长度有关，如果汽缸壁长度较短，则角区涡旋在活塞壁面方向不能充满整个活塞壁，如果汽缸壁长度较长，角区涡旋将充满整个活塞壁.

4)汽缸的尺寸比例对RCM内部的流动有着显著影响:当L/H＞3时，RCM内部会在靠近活塞壁面附近出现一对稳定的反向涡旋;当3＞L/H＞0.5时，出现一个主涡和多个辅涡共存现象，辅涡的位置与涡形成的过程有关，具有一定的随机性;当L/H＜0.5时，流动恢复一对反向涡的特征.

［1］WUMEL J，SIMMIE J M.CFD studies of a twin-piston rapid compression machine［J］.Combustion and Flame，2005，141:417-430.

［2］LEE D，SIMONE H.Rapid compression machines:heat transfer and suppression of corner vortex［J］.Combustion and Flame，1998，114:531-545.

［3］GAURAV M，CHIHJEN S.Aerodynamics inside a rapid compression machine［J］.Combustion and Flame，2006，145:160-180.

［4］GAURAV M，MANDHAPATI P R，CHIHJEN S.Computational fluid dynamics modeling for hydrogen ignition in a rapid compression machine ［J］.Combustion and Flame，2008，155:417-428.

［5］史春涛，张宝欢，金则兵，等.湍流模型的发展及其在内燃机CFD中的应用［J］.拖拉机与农用运输车，2006，33(1):5-10.

SHI Chuntao，ZHANG Baohuan，JIN Zebing，et al.Development of turbulence model and its application in the CFD of IC engine［J］.Tractor＆ Farm Transporter，2006，33:5-10.

［6］LAUNDER B E，SPALDING D B.Numerical computation of turbulent flows［J］.Computer Methods in Applied Mechanics and Engineering，1974，3(2)∶269-289.

［7］JOHN D A计算流体力学基础及其应用［M］.北京:机械工业出版社，2010:116-148.

［8］陶文铨.数值传热学［M］.西安:西安交通大学出版社，1988:500-550.

［9］王福军.计算流体动力学分析-CFD软件原理与应用［M］.北京:清华大学出版社，2004:160-182.

［10］SHUR M，STRELETS M，ZAIKOV L，et al.Comparative numerical testing of one-and two-equation turbulence models for flows with separation and reattachment［C］//33rd Aerospace Sciences Meeting and Exhibit，Reno，USA，1995:9-12.

［11］ARMALY B F，DUIST F J，PEREIRA C F，et al.Experimental and theoretical investigation of back-ward facing step flow［J］.J Fluid Mech，1983，127:473-496.

［12］郑雅芳.湍流模型的对比与叶轮机械内部气动性能的数值模拟［D］.天津:天津大学，2010:14-19.

ZHENG Yafang.The full range numerical simulation about the internal flow of turbomachinery［D］.Tianjin:Tianjin University，2010:14-19.