α-混合相依函数型数据改良核回归估计的渐近正态性
陆晓恒, 石贤汇, 凌能祥
(1.合肥工业大学 数学学院,安徽 合肥 230009;2.铜陵学院 数学与计算机科学系,安徽 铜陵 244000)
0 引言
回归函数估计是数据分析中一个非常重要的问题,由于其在通信、控制系统、模式识别等很多领域都有非常广泛的应用,一直以来备受关注。在有限维场合,很多学者无论在独立同分布(i.i.d.)还是某种相依情形下,都对其进行了研究并且获得了卓有成效的结果,如文献[1-4]等。
最近几年,随着函数型数据在包括医学、经济度量学、环境度量学、化学度量学等各个领域的广泛应用,函数型数据的回归函数估计越来越受到人们的关注。文献[5]采用经典的 Nadaraya-Watson(N-W)核,对相依数据的函数型非参数回归模型进行了研究;文献[6]建立了相依函数型数据N-W核估计的渐近正态性的性质。关于函数型数据的分析可参考文献[7-8];关于函数型数据非参数统计回归函数、条件分位数、条件众数核估计的详细分析可参考文献[9]。
设{(Xi,Yi),1≤i≤n}是同分布于(X,Y)的函数型数据,其中X在某个抽象的半度量空间E中取值,而Y取值于实值空间R。文献[5]和文献[10]引入的N-W核回归函数的估计定义为:
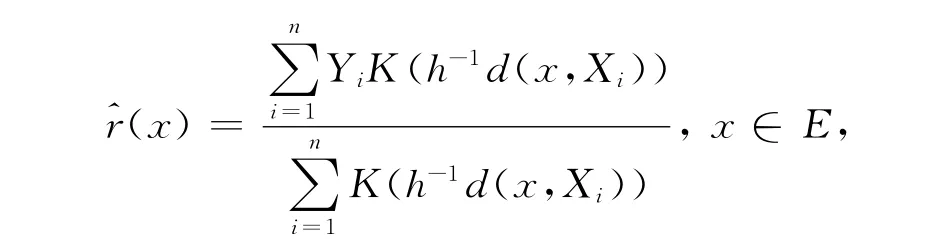
其中,K(·)为一实值的核函数;h=hn为满足的窗宽参数;d(·,·)为空间E中的一个半度量。本文所研究的改良的核回归估计为:

其中,Ι(A)是集合A上的一个示性函数;bn满足当n→∞时,bn→∞。这个估计在文献[11]中进行了研究,并得到了一些相合性的结果。
定义1 若过程{(Xi,Yi),i≥1}的混合系数α(n)满足:

则称过程{(Xi,Yi),i≥1}为α-混合或强混合过程。
其中,Akj为随机变量{(Xi,Yi),j≤i≤k}产生的σ-代数。进而,若∃a>0,C>0使得:

则称{(Xi,Yi),i≥1}为阶a的算术α-混合;若∃t∈(0,1),C>0使得:

则称{(Xi,Yi),i≥1}为几何α-混合。
本文的主要目的是就α-混合函数型数据在某些合适的条件下,获得改良的核回归估计^r(x)的渐近正态性的性质。假设C是一个正的常数,在文中每次出现时,都可以取不同的值;c1、c2为2个正的常数。
1 一些记号和假设条件
设Ki(x)=K(h-1d(x,Xi)),i=1,2,…,n;B(x,h)是中心为x,半径为h>0的小球。为了方便,先引入下列一些记号:

(1)(i)∀h>0,P{X∈B(x,h)}=φx(h),其中且φx(h)在原点的某个领域内关于h绝对连续。
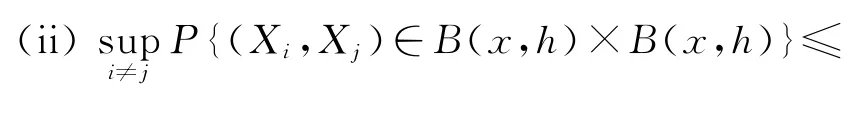

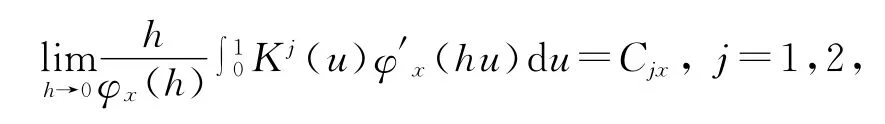
其中,Cjx,j=1,2为2个正的关于x的函数。
(3)对v≥1,都有E|Y|v≤C<∞。
(4)(i)∃β>0,使得对∀μ,ν∈E,有|r(μ)-r(ν)|≤Cd(μ,ν)β。
(ii)设g2(u)=Var[Yi|Xi=u],u∈E,在x的某个领域内连续且满足当h→0时,

(2)K(·)是满足0<c1≤K(·)≤c2<∞的支撑集为[0,1]的实值核函数,且满足:
设对某个m>2有:
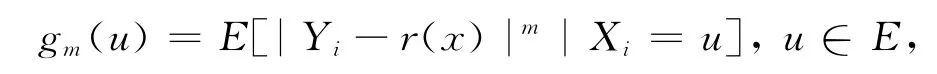
在x的某个领域内连续。
(iii)设g(u,v;x)=E[(Yi-r(x))(Yjr(x))|Xi=u,Xj=v],i≠j,u,v∈E在(x,x)的某个领域内连续。
(5)对某个m>2,p>1-2/m有:

(6)设当n→∞时有nφx(h)→∞。同时存在正整数序列{vn}满足
条件(1)和文献[6]中的condition 3′不同,这里小球概率和联合密度函数都没有写成2个函数乘积的形式,更具一般性。条件(2)关于核函数的假设是很经典的,关于极限值的假设在文献[6]和文献[11]中都作了类似的假设。条件(3)~(6)都可以在文献[6]中找到类似的假设。
2 结论及其证明
为了更方便地叙述和得到相关结论,先给出一些引理,并对其进行证明。

证明 由文献[11]中Theorem 2的证明过程可知:于是根据un(x)的表达式可得:


首先对T1进行处理:

同时有:

由条件(4)的(i)可知:

于是,由条件(2)可得:
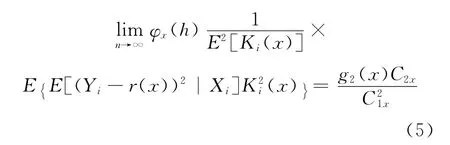
又由控制收敛定理知,当n→∞有:

因此,由(3)式、(5)式、(6)式有:
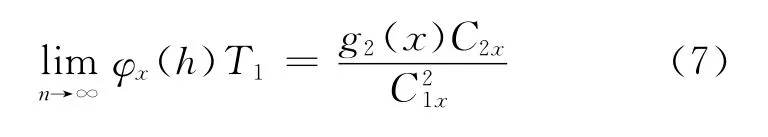
对T2进行处理:
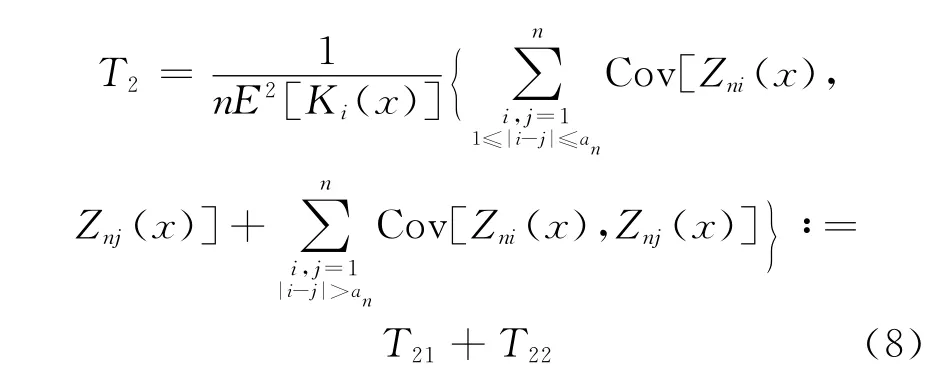
其中,an=o(n),下面将给出其具体形式。
对于T21:
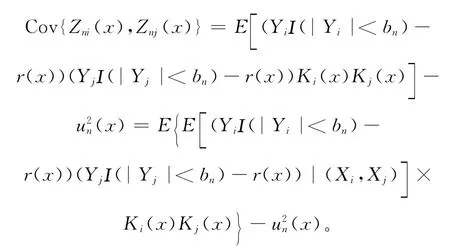
由控制收敛定理知,当n→∞有:

又由条件(1)的(ii)、条件(2)和条件(4)的(iii),当n足够大的时候,可得:
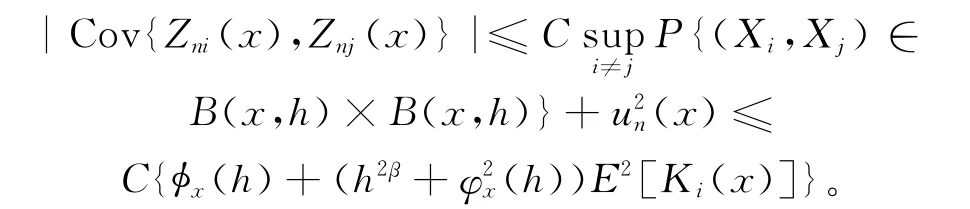
从而当n足够大的时候有:

对于T22,利用文献[12]中Davydov’s lemma可得:
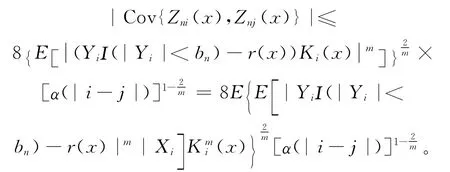
由控制收敛定理知,当n→∞有:
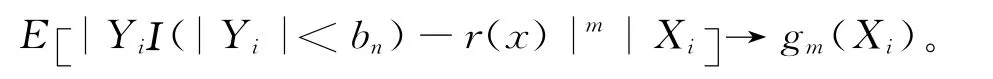
又由条件(2)和条件(4)的(ii),当n足够大的时候,可得:


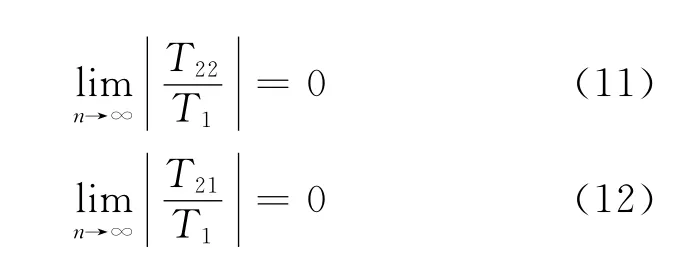
综上(2)式、(7)式、(8)式、(11)式和(12)式,于是有:

引理2 假设条件(1)~(6)满足,则当n→∞时有:
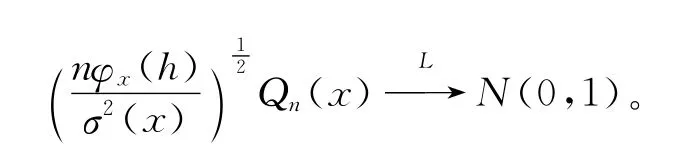
证明 此引理的证明利用Bernstein大块小块过程,可参考文献[6]中Theorem 4的证明。
引理3 假设条件(1)、(2)和(5)满足且有,则
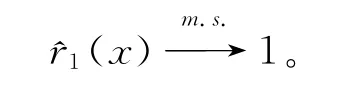
证明 此引理的证明参见文献[6]中Theorem 1的证明,需要注意的是小球概率和联合密度函数的表达形式不同。
引理4 假设条件(1)~(6)满足,则当n→∞时有:
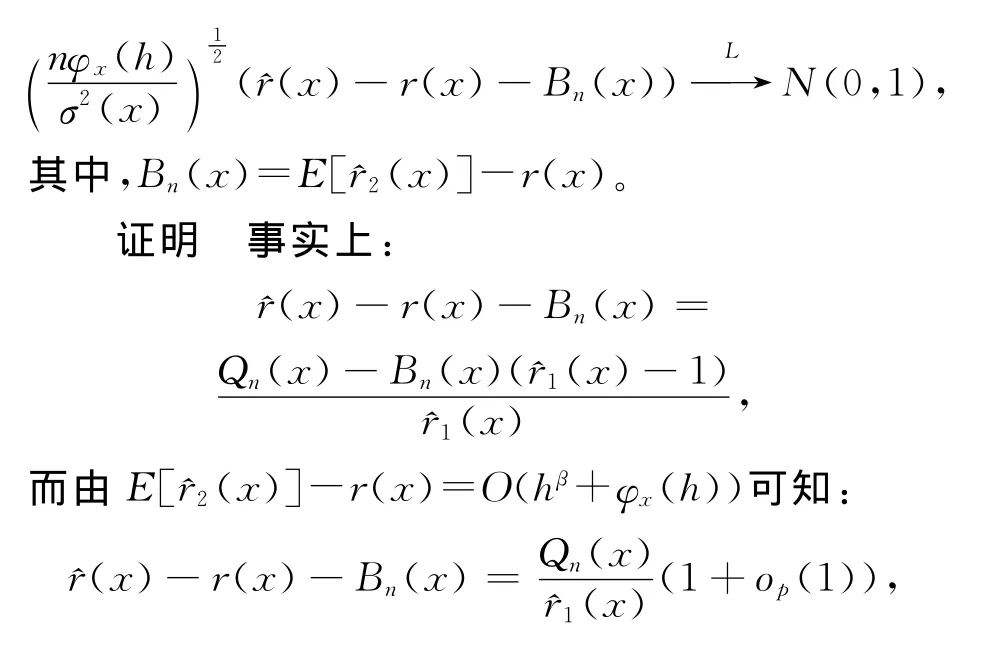
于是由引理2和引理3可知结论成立。
下面给出本文的一个重要结论。

[1]Devroye L.On the almost everywhere convergence of nonparametric regression function estimate[J].The Annals of Statistics,1981,9:1310-1319.
[2]Roussas G G.Nonparametric regression estimation under mixing conditions[J].Stochastic Process Appl,1990,36:107-116.
[3]Roussas G G,Tran L T,Ioannides D A.Fixed design regression for time series:asymptotic normality[J].Journal of Multivariate Analysis,1992,40:262-291.
[4]Tran L T.Nonparametric function estimation for time series by local average estimators[J].The Annals of Statistics,1993,21:1040-1057.
[5]Ferraty F,Vieu P.Nonparametric model for functional data with application in regression,time series prediction and cure discrimination[J].Journal of Nonparametric Statistics,2004,16(1/2):111-125.
[6]Masry E.Nonparametric regression estimation for dependent functional data:asymptotic normality[J].Stochastic Process Appl,2005,115:155-177.
[7]Ramasy J,Silverman B.Functional data analysis[M].New York:Springer,1997:68-90.
[8]Ramasy J,Silverman B.Applied functional data analysis:methods and case studies[M].New York:Springer,2002:42-78.
[9]Ferraty F,Vieu P.Nonparametric functional data analysis:theory and practice[M].New York:Springer,2006:36-174.
[10]Ferraty F,Vieu P.The functional nonparametric model and application to spectrometric data[J].Comput Stat,2002,17:545-564.
[11]Ling N,Wu Y.Consistency of modified kernel regression estimation for functional data[J].Statistics,2010.doi:10.1080/02331888.2010.500077.
[12]Hall P,Heyde C C.Martingale limit theory and its applications[M].New York:Academic Press,1980:23-52.

