Lagrange插指与Newton插指的注记
邹 乐, 李昌文
(1.合肥学院 网络与智能信息处理重点实验室,安徽 合肥 230601;2.淮北师范大学 数学科学学院,安徽 淮北 235000)
0 引言
插值在工程数值计算方面有着广泛的应用,如有限元方法中形函数的建立、科学计算可视化过程中图形图像的实现等都要用到插值理论。插值问题的实质是希望找到一个尽量简单的函数,如多项式函数去近似某个函数。然而对于有些问题,多项式函数虽然简单,却不便于计算,如求参数的最大似然估计值,为解决此问题,文献[1-5]提出了幂指数插值,简称插指。Lagrange插值公式构造简单、结构紧凑、思路清晰,但缺点是在等距结点插值过程中,当结点数较大时会表现出极大的数值不稳定性。此外,当插值结点的个数有变动时,Lagrange插值公式也随之发生变化,需重新构造,从而整个公式的结构也发生变化,这在实际计算中是极不方便的。为了克服上述缺点,文献[6-8]给出了2种解决办法:利用与之等价的Newton插值多项式进行计算;对传统的Lagrange插值进行改进,提出了改进的Lagrange插值和重心Lagrange插值。
本文对Lagrange插指多项式进行改进,提出了一种改进的Lagrange插指和重心型Lagrange插指,并讨论了Lagrange插指多项式与Newton插指多项式的相互转化问题。
1 Lagrange插指与Newton插指
1.1 Lagrange插指
设给定函数y=f(x)及在区间[a,b]上的一组对应关系{(x0,y0),(x1,y1),…,(xn,yn)},以n+1个n次Lagrange插值基函数为基础,文献[2]构造出Lagrange插指多项式,并证明了次数不超过n的插指多项式唯一性。
文献[2]构造的Lagrange插指公式为:
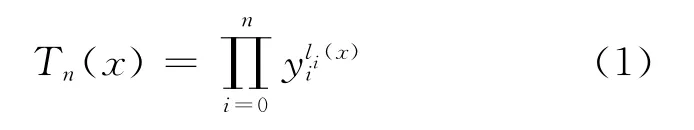
其中,li(x)为在n+1个节点上的n次基本插值多项式,或称作n次Lagrange插值基函数,即
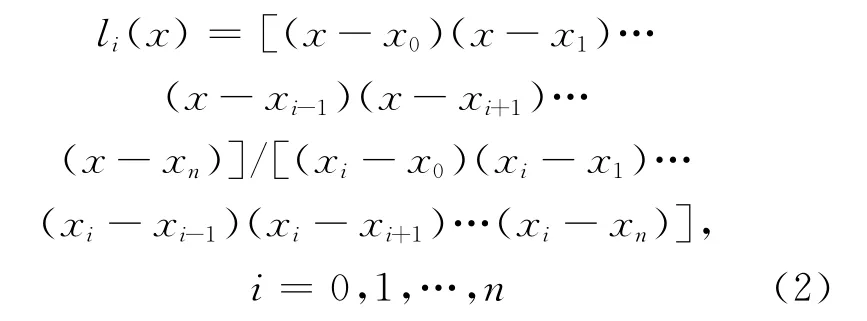
同Lagrange插值多项式一样,Lagrange插指多项式在插指结点较少时,具有很好的插值精度,其存在的主要缺陷是:① 增加新的插指结点时,需要重新计算;② 当结点数量很大时,插指是数值不稳定的。
1.2 Newton插指
设函数y=f(x)及在区间[a,b]上有定义且大于零,给定区间[a,b]上的一组对应关系{(x0,y0),(x1,y1),…,(xn,yn)},文献[1]证明了存在唯一的一个n次Newton插指多项式,即

满足插指条件:

其中,ai(i=0,1,…,n)为差商指;pi(x)=(xx0)(x-x1)…(x-xi-1),i=0,1,…,n。
2 改进的Lagrange插指与重心型插指
2.1 改进的Lagrange插指
(2)式的插值基函数li(x)的分子可以写成:

定义重心权为:
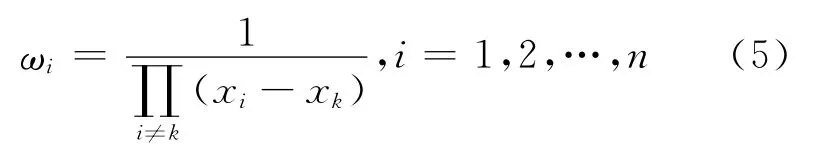
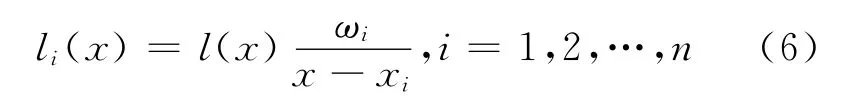
将(6)式代入(1)式,得到Lagrange插指公式的另一种表现形式为:)

(7)式称为改进的Lagrange插指公式,在增加一个新的插指节点时易于计算。
2.2 重心型Lagrange插指
利用Lagrange插值多项式插值常数1,可以得到的恒等式为:
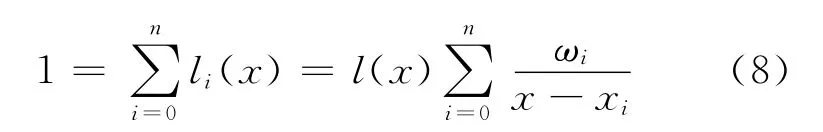
利用(8)式可得到重心型Lagrange插指公式为:
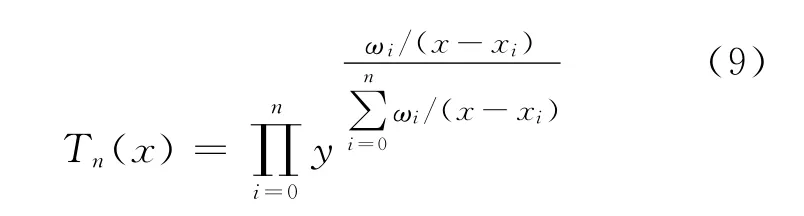
重心型Lagrange插指多项式在分子和分母都包含插值权ωi,因此ωi的任何非零倍数仍是插值权。由(5)式可知,插值权仅依赖于插值结点的分布,因此对于一些特殊的结点分布可以得到简化插值权。
3 插指的相互转化
下面讨论Lagrange插指与Newton插指的相互转化算法。由(1)式得:
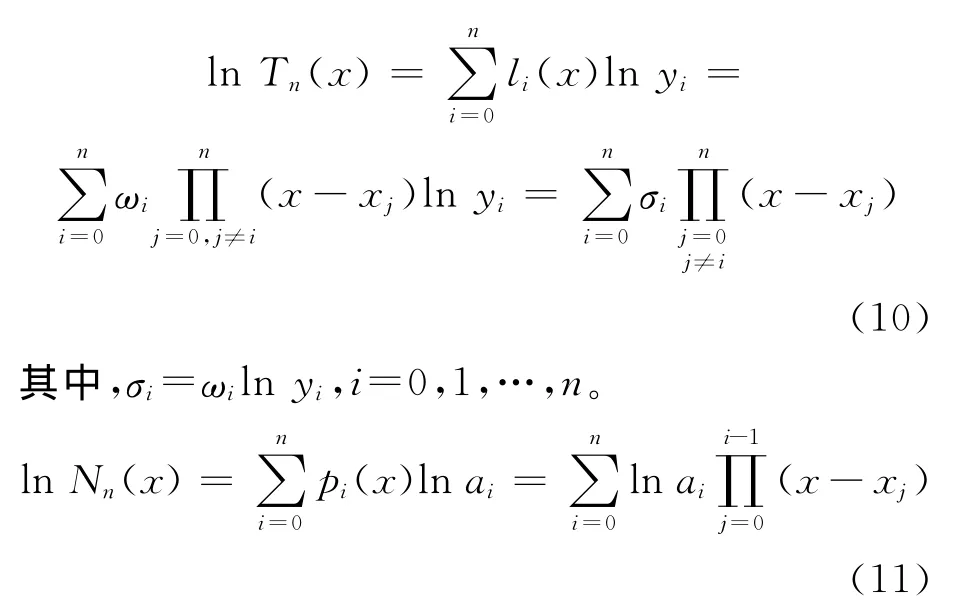
其中,ai(i=0,1,…,n)是差商指;pi(x)=(xx0)(x-x1)…(x-xi-1),i=0,1,…,n。
差商可以由函数值线性组合表示[9],可得:
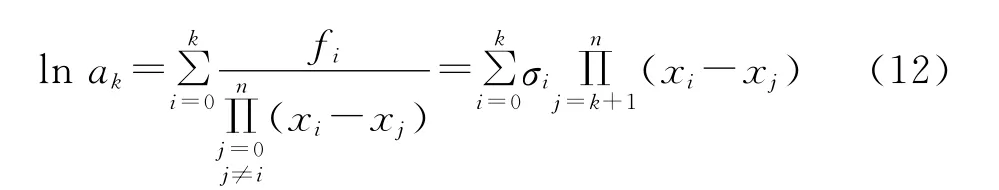
因此,由Newton插指与Lagrange插指的转化变成如下线性方程组的解,即
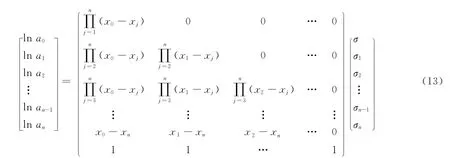
利用Gauss消去法可得如下算法:
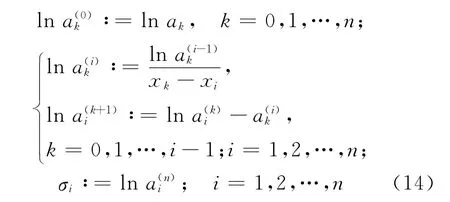
上述线性方程组也可以用作由Lagrange插指向Newton插指的转化算法。给定形如(10)式的Lagrange插指多项式可以计算Newton插指多项式(11)式中的系数ai。
如果当i≠j时xi≠xj,可以得到由Lagrange插指向Newton插指的转化算法为:

4 数值例子
以Runge函数f(x)=1/(1+25x2)为例,说明重心型Lagrange插指多项式的良好数值稳定性。在区间[-1,1]上令n=100,以第2类Chebyshev点作为插指节点,插指计算区间[-1,1]上的2 000个点的近似值,利用 Matlab绘图,如图1所示。
通过大量的数值计算表明,对于等距节点重心Lagrange插指表现出极大的数值不稳定性,但是对于Chebyshev点的插指,重心型Lagrange插指具有极好的数值稳定性。
下面的例子说明了由Lagrange插指向New-
ton插指转化算法的有效性和可行性。

图1 Runge函数的重心型Lagrange插指
例1 求满足插指条件:y0=f(0)=(1-p)2,y1=f(1)=2p(1-p),y2=f(2)=p2的插指公式,其中0<p<1[3]。
由文献[2]易得满足插指条件的Lagrange插指为:

由此可得:

易见:
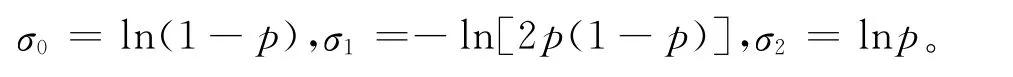
由Lagrange插指向Newton插指的转化算法(15)式可得:
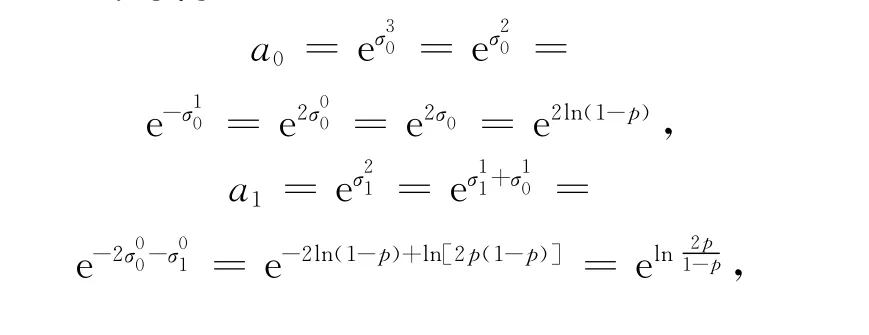

故可以直接写满足插指条件的Newton插指为:
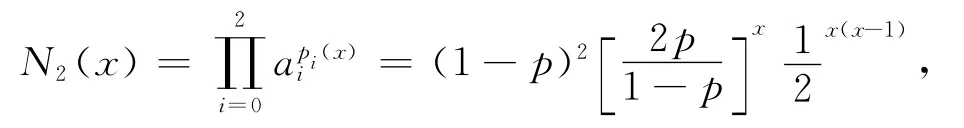
这与用文献[1]中方法所求结果完全相同,由Newton插指向Lagrange插指的转化算法(14)式可以由a0、a1、a2计算出σ0、σ1、σ2。
5 结束语
本文改进了Lagrange插指多项式,得到2种新形式的插指多项式:改进的Lagrange插指多项式和重心型Lagrange插指多项式。当增加新的插值节点时不需重新计算原有插指节点的Lagrange基函数。文中讨论了Lagrange插指多项式与Newton插指多项式的相互转化,给出了由Newton插指多项式向Lagrange插指多项式的转化算法以及由Lagrange插指多项式向Newton插指多项式的转化算法。
[1]颜宁生.牛顿(Newton)插指[J].大学数学,2006,22(5):107-113.
[2]颜宁生.Lagrange插指[J].北京服装学院学报,2005,25(3):50-56.
[3]颜宁生.连幂式插值[J].数学理论与应用,2009,29(3):103-105.
[4]邹 乐,唐 烁.二元Newton插指[J].合肥工业大学学报:自然科学版,2010,33(2):304-307.
[5]王兆清,李淑萍,唐炳涛.一维重心型插值:公式、算法和应用[J].山东建筑大学学报,2007,22(5):448-453.
[6]王兆清,李淑萍,唐炳涛.任意连续函数的多项式插值逼近[J].山东建筑大学学报,2007,22(2):158-162.
[7]Berrut J P,Trefethen L N.Barycentric Lagrange interpolation[J].SIAM Review,2004,46(3):501-517.
[8]Werner W.Polynomial interpolation:Lagrange versus Newton[J].Math Comp,1984,43(167):205-217.
[9]徐士良.计算方法[M].北京:人民邮电出版社,2009:128-130.

