核电结构设计中参数不确定性对楼层谱计算影响分析

李 建 波， 林 皋， 钟 红， 胡 志 强

（大连理工大学 建设工程学部 工程抗震研究所，辽宁 大连 116024）

0 引 言

核电建设的安全性受到日益广泛的关注，这就更要求处理好安全与经济的关系，使设计出的结构具有足够的安全性，但又是适宜的和经济的.

核电厂房的楼层反应谱是核电结构和设备抗震设计的依据.在当前核电厂结构设计中，楼层反应谱一般采用确定性的方法进行计算.实际上核电结构承受的环境荷载及其性能参数可能在很大的范围内发生变化，确定性计算只能选择可能性比较大，同时又相对保守的参数进行分析，这样对计算结果反映实际情况的程度就很难作出可靠的判断.

核电厂楼层反应谱计算中不确定性因素大体上可以分为3类[1、2].第1类属于计算模型的不确定性范畴.核电厂结构设计中采用不同的模型进行离散.不同的离散和简化途径及方法对楼层反应谱计算结果的影响是否偏于安全方面，是难以作出可靠判断的.第2类属于结构和地基性能参数的不确定性范畴，其对楼层反应谱的影响是否偏于安全不能事先确知.这些参数包括地基的剪切模量、结构的弹性模量等.第3类也属于结构和地基性能参数的不确定性范畴，其对楼层谱计算结果的影响是否偏于安全，其趋向是肯定的.这类参数包括地震动输入的加速度、结构的阻尼等.种种不确定性的组合对楼层反应谱的影响，用确定性的方法进行分析难以奏效，采用不确定性的分析方法则可以获得更为合理的结果.只是不确定性分析方法目前仍处于发展阶段，同时计算工作量也比较大，所以应用尚不普遍.

考虑不确定性影响的随机分析目前进行的研究大体上可区分为两类.一类假定结构是确定性的，只是考虑地震动等输入的不确定性，据此计算结构的响应即输出的不确定性影响，计算相对比较方便.另一类则考虑结构本身的不确定性，有的采用试算法，有的采用随机概率法，以随机有限元方法为代表，直接在结构动力方程中增加体现结构动力特性变异性的参数及其概率分布规律，再经由数值求解获得响应最优解及其变异系数[3～7].该类方法一般需要将不确定性参数的概率密度函数假设为正态分布或均匀分布等简单形式以便于处理，同时不确定性参数的数量也不宜过多.像核电厂结构这样的复杂随机系统，所含的不确定性参数种类繁多，要在随机分析理论基础上建立相应的计算模型在当前的技术条件下是比较困难的.本文结合我国核电工程抗震安全检验的客观需要，适应土－结构动力相互作用时程分析相关模型的最新发展，参考美国核电设计规程的建议[1]，采用基于蒙特卡罗模型的概率统计法进行核电厂结构楼层反应谱的分析.这是在确定性分析的框架内，选取核电结构的主要变异性参数（含计算荷载的变异性、材料性能的变异性等）及其概率分布规律，通过对数值结果的概率统计，获取不同置信率的响应结果.即对传统的确定性方法获得的动力响应结果进行置信率的定量判断，以便对传统确定性方法设计的核电结构的安全性有更为深入的了解.的勘测数据进行拟合调整.由于采用概率统计方法，可以适应各种形式表示的概率密度曲线，并不要求具有解析表达式.当数据不够充分时，也可以近似地采用正态分布，甚至均匀分布曲线，生成随机样本.

1 核电结构设计中不确定性因素及其计算模型

核电结构设计中对楼层谱计算有影响的参数都在一定范围内发生变化，美国核电设计中建议的设计参数的概率密度变化函数如图1所示.该图主要依据的是少量测试数据的统计结果，仅在缺少实测数据条件下可以引用.更为确切的方法是针对不同的厂址条件进行具体试验测定.图中R代表随机值与确定值的比率，其中R＝1为确定性设计中的采用值.括号中的数值则代表超越概率10%和90%，是偏离中值的比例.结构材料和地基土的阻尼通过结构－地基动力相互作用对楼层谱的计算发生重要影响，地基土的阻尼比可在很大范围内变化，它不仅包括地基土的材料阻尼，还包括地震波向无限远处扩散的辐射阻尼影响.结构材料的阻尼中，常用混凝土和钢筋阻尼的变化特点各不相同.地基对楼层谱计算产生的另一重要影响，是其剪切波速所代表的地基剪切模量的不确定性.这包括地基本身的不均匀性，以及不同勘测单位采用的勘测设备不同所可能产生的离散性.结构构件，如剪力墙、梁、柱等的计算参数，如惯性矩、剪切面积、弹性模量以及节点质量等也都在一定范围内变化.

此外还有地震动输入的不确定性，将另文进行讨论.这些概率密度分布曲线可以根据各工程

图1 不确定性参数的概率分布Fig.1 Input probability distribution of indeterministic parameters

2 楼层反应谱的计算分析

进行核电结构楼层反应谱的计算时，核电结构常采用多质点弹簧、阻尼体系分析.为了更好地反映结构特点以及结构和水相互作用的影响，有限元方法也逐渐得到应用.

楼层反应谱的计算，时程积分是比较直接和常用的方法.其构造与设计反应谱相匹配的人工地震波作为输入，计算结构支撑点的地震响应，再据此得到楼层反应谱.但时程分析不能得到光滑的楼层反应谱.对此，不同的研究者提出不同的看法.Biggs等认为时程分析获得的楼层谱不可靠[8].核电规程委员会（NRC）在早期未发表的一份备忘录中曾经对在核电厂设计中采用时程分析法构造楼层反应谱提出过批评[9].美国新的核电规程ASCE－98对时程分析还是给予了肯定.但在概率统计分析方面，则计算工作量比较大.

另一种求解楼层反应谱的方法是从地震动的设计反应谱直接计算楼层反应谱，许多研究者提出了不同的方法.Biggs等[8]和 Kapur等[10]鉴于将主附结构系统简化为两自由度体系进行分析的基本思想，推导了附属结构的响应作为楼层谱计算的依据，并经过若干实际核电结构的检验，证明其计算简便.但由于所采用的假定，计算结果偏于保守.Singh[11]则将地震动输入作为平稳随机过程进行考虑，推导了核电结构支承的振子的随机响应，得出楼层反应谱值.其计算结果精度比较高，但在共振峰处出现偏差，后来又作了进一步改正[9]，达到了良好的效果.所有这些方法都是鉴于刚性地基的情况进行的推导，没有考虑结构与地基相互作用的影响.

本文采用从地震动输入反应谱直接计算楼层反应谱的方法.由于主要研究参数不确定性对楼层反应谱的影响，比较确定性分析与不确定性分析结果的差别，选用了比较简单而又方便的Biggs方法进行楼层反应谱的计算.Biggs方法的基本思想是当振子（附属结构或设备）刚度相对于主体结构刚度较大时，则振子最大加速度相对于地面运动加速度的动力放大系数β主要取决于主体结构的振动放大特性；而当振子相对于主体结构柔度较大时，则主体结构的振动放大特性对振子的动力放大系数影响较小，可近似地看作将振子直接放置于地面上来计算振子的动力放大系数.令Aemn表示振子相应于主结构n阶模态的最大加速度；Asne＝｜Aonηsnsne｜，为主结构第n阶模态在子系统支承点的最大加速度；Aeg表示地面运动的最大加速度；Aon为主结构第n阶模态周期处的地震动输入反应谱值；Tem表示振子的振动周期；Tsn表示结构第n阶模态的振动周期.Biggs方法对楼层反应谱的计算可表述如下：

当Tem/Tsn≤1.25时

当Tem/Tsn＞1.25时

根据主结构阻尼比ζs和附属结构阻尼比ζe的取值，系数β1可按图2求得，系数β2则可按图3求得.A′em或A″em针对主结构的每一模态进行计算，然后加以综合.令符合式（1）的主结构模态数为n′，符合式（2）的主结构模态数为n″，主结构第n阶模态的参与系数为ηsn，振子所在部位的主结构模态值为sn，则振子最大加速度的综合值为

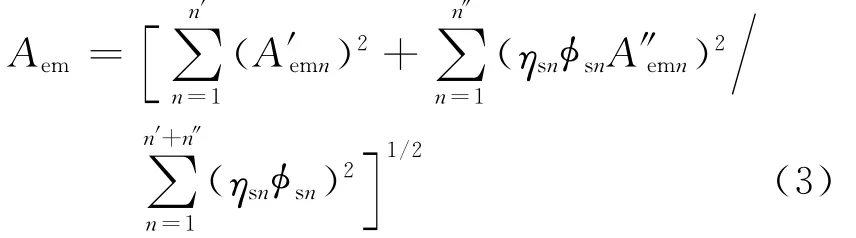
如附属结构或设备为多自由度系统时，则附属结构计算点的最大加速度可表示为

图2 按结构振动特性确定的放大系数Fig.2 Magnification ratio based on structural dynamic properties

图3 按地面运动特性确定的放大系数Fig.3 Magnification ratio based on ground motion

式中：ηemr为附属结构r阶模态的参与系数；emr为附属结构计算点第r阶模态的模态值.将附属结构的各模态响应按平方和开根的方法求得综合响应.＝1.2×1010Pa，泊松比ν＝0.30，剪切波速vs＝2150 m/s.地震动输入方面，限于篇幅，主要考虑水平向地震动的作用，采用1/2 SSE设计水准，对应的水平向地震动峰值为9 m/s2.按图5所示地震动厂址谱作为输入.

3 考虑参数不确定性的楼层谱概率统计分析方法

考虑设计参数不确定性，对楼层反应谱进行概率统计分析的实现方法可简化如下.依据表征输入参数不确定性的概率分布密度函数，通过生成随机数建立起各项参数的样本空间；再以结构确定性抗震分析为基本过程，获得各组随机样本对应的楼层反应谱结果；最后对该结果进行统计处理，获得概率意义上的统计楼层谱计算值.这一过程中，输入参数与输出楼层谱结果的统计处理可按相同的保证率进行.

具体随机样本生成过程中，主要以分布密度函数的形式来控制各不确定性参数的随机样本取值情况，其中包括场地剪切波速、结构动弹性模量、构件剪切模量、转动惯量、节点质量等值.而分析过程中，地震荷载与确定性分析过程保持一致，按确定值处理.

此外，由于随机样本参数的生成不能事先保证其满足指定的范围要求，实践中，可根据工程设计的需要来取舍.如根据3d原则（d代表标准差），参数取值在此范围内的保证率为0.997.据此，对随机样本数据进行筛选，超出该范围，可认为是不可能事件.

4 算例与分析

以某百万千瓦级压水堆核电站反应堆厂房RX为背景，其多质点简化模型如图4所示.结构的材料为混凝土，动弹性模量为4×1010Pa，剪切模量为1.6×1010Pa，泊松比为0.2，质量密度为2500 kg/m3，阻尼比为7%.

确定性厂房楼层反应谱计算中，假设如下均质场地参数：密度ρ＝2600 kg/m3，动剪切模量G

图4 反应堆厂房（RX）集中质量计算模型Fig.4 Lumped mass model for the RX plant

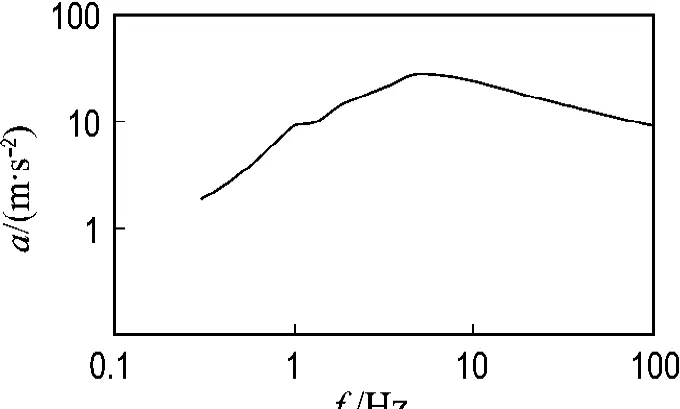
图5 确定性数值分析水平向输入加速度反应谱Fig.5 Horizontal seismic input acceleration spectra for the certain numerical analysis

进而，按本文方法，将输入地震动保持定值（地震动不确定性的影响另文进行讨论），考虑模型及地基动力参数的不确定性，进行厂房地震响应的随机数值分析，并将反应谱概率统计结果与确定性分析结果进行比较.

4.1 样本空间数量的选取

为了进行楼层谱统计学意义上的分析与处理，选取大数量（N组）的随机样本空间是必要的.

分别按100组、200组、300组、400组及500组样本组合，在题设2%阻尼条件下，对比反应堆厂房某高位点的水平向楼层反应谱90%保证率的统计结果.

经过比较发现，100组随机数列样本组合与200～500组样本组合，概率统计结果相差无几，说明100组即可满足收敛精度要求.为避免在随机统计过程中因组合数过少引入其他的数值不确定性因素，后续结果将统一按300组随机样本空间进行参数输入计算与楼层谱结果的统计分析.

4.2 楼层谱数值结果比较与分析

由于篇幅所限，此处仅给出图4所示厂房结构节点8（即安全壳结构50.02 m标高）和节点12（内部结构29.00 m标高）处的楼层加速度反应谱曲线的对比.

为进行确定性分析与不确定性概率统计分析的对比，在图6中，楼层谱确定性分析与概率统计分析均以相同的地震动时程作为外荷载输入.图6（a）表示2%阻尼比条件下，厂房8号节点处水平向楼层反应谱确定性数值计算结果与90%、99%保证率的楼层谱概率统计结果的对比.很明显，概率统计结果与确定性分析曲线相比，两者形状较为接近，只是在楼层谱峰值区段有一定幅度的降低.而且99%保证率的概率统计楼层谱相比90%保证率的结果要大，这与本文的定性判断相一致.按国际主要核电参考规范ASCE 4－98的相关规定[2]，从统计学意义上考虑，满足90%保证率的反应谱，即可认为符合安全要求.进而，图6（b）针对厂房结构12号节点处的楼层谱，给出了2%、5%、10%不同阻尼比条件下确定性计算值与90%概率统计结果的对比，其相对关系与图6（a）基本类似，只是峰降率随着阻尼比的增加而降低.具体表现为90%保证率条件下，与图6（a）及图6（b）相对应的反应谱峰降率统计如表1所示.不难看出，其与ASCE规范关于参数不确定性对楼层谱影响的论述相一致，即小阻尼条件下，在满足90%保证率的前提下，峰降幅度可能进一步降低，甚至远大于15%[1、2].

从楼层反应谱的曲线形态上来看，基于结构－地基动力相互作用的数值分析，2%～10%低阻尼比条件下，90%保证率的概率统计分析结果同确定性模型分析结果相比在低频与高频段较为接近，而在峰值段降低明显，且更为光滑.确定性分析与本文概率统计分析得到的楼层反应谱已应用于核电厂地基适应性的评价，其相关成果可相互印证.

图6 楼层反应谱计算值曲线Fig.6 Numerical results curves of the floor response spectra

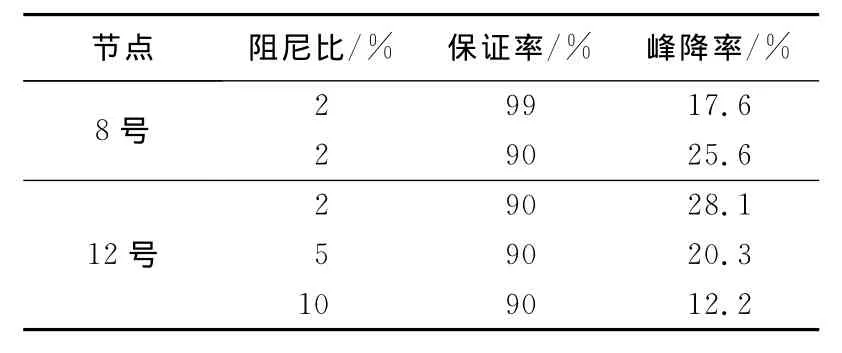
表1 概率统计楼层谱计算结果峰降率Tab.1 Decrease range for the probabilistic peak values of the floor response spectra

5 结 论

本文结合结构抗震时程分析法的最新发展，在考虑土－结构动力相互作用的基础上，提供了一种可供参考的确定性与概率统计法相结合的楼层谱计算方法.该方法可不受模型不确定性参数的个数与统计参数概率分布规律的限制.计算中以概率统计分析为基本手段，通过定义不同的概率密度函数来研究输入参数的不确定性对楼层谱计算值的影响，为核电站的抗震设计裕量评估和安全管理提供了一些可资参考的有益结论.

本文研究也表明，确定性分析获得的反应谱具有足够的安全裕度，即相关结果具有足够的可靠度和保守性.同时，通常情况下，低阻尼比条件下，按照现行的国际主要核电抗震规范，通过包络和按结构频率的0.15倍拓宽与降低峰值来考虑参数不确定性对楼层反应谱的影响也是可行的[2]、保守的.

[1]ASCE.Seismic analysis and design[M]//Structural Analysis and Design of Nuclear Plant Facilities.New York：ASCE，1980

[2]ASCE. ASCE 4－98 Seismic Analysis of Safety－Related Nuclear Structures[S].New York：ASCE，2000

[3]李忠献，李忠诚，梁万顺.考虑土－结构相互作用和岩土参数不确定性的核电厂结构地震响应分析[J].地震工程与工程振动，26：143－148

[4]LIAMBIA J M，SHEPHERD D J，RODWELL M D.Sensitivity of seismic structural responses to interpretation of soils data [J].Soil Dynamics and Earthquake Engineering，1993，12（6）：337－342

[5]WU W H，SMITH H A.Efficient model analysis for structures with soil－structure interaction [J].Earthquake Engineering ＆Structure Dynamics，1995，24：283－299

[6]张建霖，杨智春.随机输入条件下的楼层反应谱分析[J].西北工业大学学报，2003，21（6）：651－653

[7]PARK Y J，HOFMAYER C H，CHOKSHI N C.Survey of seismic fragilities used in PRA studies of nuclear power plant[J].Reliability Engineering and System Safety，1998，62：185－195

[8]BIGGS J M，ROESSET J M.Seismic analysis of equipment mounted on a massive structure[M]//HANSEN R J，ed.Seismic Design for Nuclear Power Plants.Cambridge：MIT Press，1970

[9]SINGH M P.Seismic design input for secondary systems [J].Journal of the Structural Division，ASCE，1980，106（2）：505－517

[10]KAPUR K K，SHAO L C.Generation of seismic floor spectra for equipment design [C] //Proceedings of ASCE Specially Conference on Structural Design of Nuclear Plant Facilitation.Chicago：ASCE，1973：29－71

[11]SINGH M P.Generation of seismic floor spectra[J].Journal of the Engineering Mechanics Division，ASCE，1975，101（5）：539－607