柔性结构技术在精密工件台中的应用

齐芊枫，郑椰琴，吴立伟，方 洁，董俊清

(上海微高精密机械工程有限公司，上海 201203)

微纳米加工技术的发展，尤其是各种光刻技术的发展，离不开精密工件台技术的发展和进步。精密工件台直接影响光刻机所能实现的特征线宽尺寸和生产效率，所以光刻技术的更新与新一代光刻机的研制必然对工件台提出更高的要求，主要表现在精度、运行速度和行程等方面。

新一代光刻机对工件台大行程、高精度等的要求使得机械设计工程师们总是在寻找高刚性结构设计方案。他们往往认为高刚性的结构设计才能达到更高的精度。然而，这样的结构设计通常会受到很多因素的影响，例如：无形的误差（可动载荷、振动、热以及不稳定性等）、高制造成本、对设备的高要求等。

相反，柔性的机械结构具有的特性：较低的力可传递性、较低的成本、较轻的质量及较小的空间占有率。同时，可最大限度地增加柔性结构的比率以达到合适的性能、成本和质量，即柔性结构可简化机器构造。

1 刚性结构设计

刚性结构设计要求零部件有很高的加工制造精度和装配精度，因此对加工设备、装配工装工具以及人员都提出了严格的要求；同时，刚性结构易传递振动、热等，从而影响结构性能；另外，刚性的结构设计容易引入附加的力和转矩，对材料的刚度和强度提出了更高的要求。

典型的“H”型工件台结构如图1所示，是由2个y方向导轨和1个x方向导轨组成，可平面运动。若x向导轨和y向滑块采用完全刚性连接，则要求y底面导轨和侧向导轨具有很高的垂直度和平面度，从而对材料的稳定性、零件加工精度和导轨的装配提出了更高的要求。同时，当2个y向滑块不同步运动时，也会对x向导轨产生附加力和力矩。

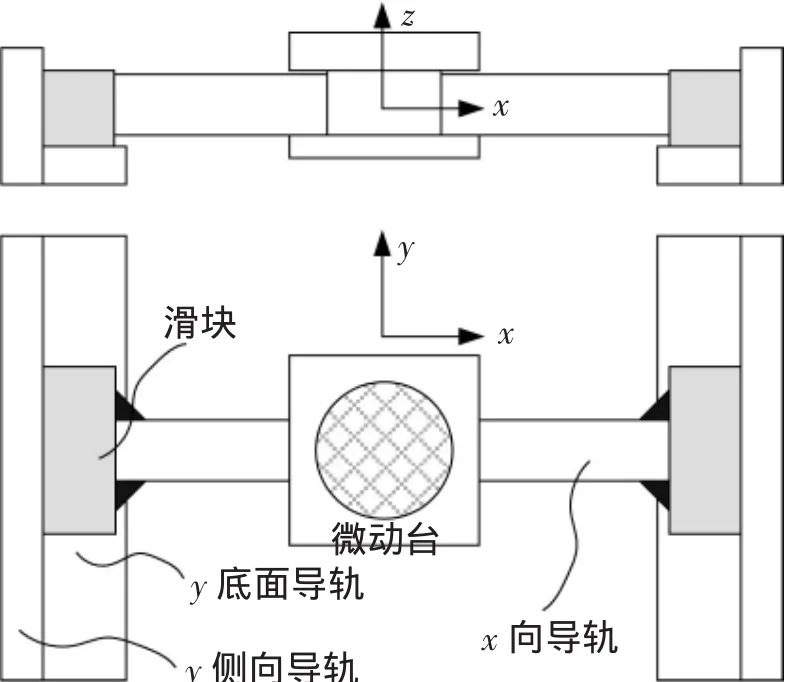
图1 刚性“H”型工件台结构

2 柔性结构设计

与刚性结构相比，柔性的结构设计不仅可以降低加工和装配的成本，同时可提高精度，并且还能消除机械摩擦和空回行程等。目前，柔性的结构设计广泛应用于微位移平台、超精密机械加工、微夹持器、加速度计、陀螺仪、扫描隧道显微镜、运动导轨、导弹控制装置、高精度照相机等。

柔性结构的工件台结构如图2所示，在y向滑块与侧向气浮垫之间设计复合柔性件结构Rz簧片，该柔性件结构具有Rz的自由度，可对两个y向电机的不同步运动进行解耦。另外，在x向导轨与y向滑块相连处应用柔性结构Ry簧片，通过柔性簧片的变形可消除两个y向底面导轨上端面不平行产生的间隙或装配应力等。

图2 柔性“H”型工件台结构

3 柔性件设计与计算

将柔性结构设计技术应用于工件台，最主要的是进行柔性件的设计与计算。通常利用有限元分析技术，结合铰链强度、刚度、工作台的动态特性等条件，设计柔性铰链的结构和尺寸。有限元分析技术计算工作量大、耗时长，因此本文根据对不同结构形式柔性件的分析比较，选取适用于工件台的柔性件结构形式，并结合柔性件基于弹性静力学的理论公式，进行柔性件设计和数值计算，并通过将计算结果与有限元分析结果比较，找寻适用于工件台的柔性件结构设计和计算方法。

3.1 柔性件的结构形式

文献 [1]中，将柔性件分为5种常见结构形式，主要是直梁型柔性件、倒圆角直梁型柔性件、椭圆型柔性件、抛物线型柔性件和双曲线型柔性件等，（通常，我们将直梁型柔性件和倒圆角直梁型柔性件称为柔性簧片，其它结构形式的柔性件称为柔性铰链）。其中直圆型柔性铰链是椭圆型柔性铰链的一种特例，见图3。影响柔性铰链刚度的参数有很多，例如柔性特征的宽度，最小凹口厚度，切口半径以及材料的弹性模量。

图3 五种常见柔性件的结构

根据文献[1]中柔性件拉伸刚度的计算结果，抛物线型柔性铰链具有最大的轴向拉伸刚度，柔性簧片具有最小的轴向拉伸刚度，抛物线型柔性铰链、双曲线型柔性铰链和椭圆型柔性铰链的拉伸刚度明显大于柔性簧片，并且直圆型柔性铰链在相同铰链厚度和长度的情况下具有最高的精度。双曲线型柔性铰链具有最大的转动刚度，柔性簧片具有最小的转动刚度，并且柔性簧片的转动刚度明显小于其它三种柔性铰链。

柔性簧片具有较小的转动刚度，直圆型柔性铰链具有最高的精度，并且，这两种形式的柔性铰链计算相对简单，因此，在工件台的柔性结构设计中，一般选用这两种形式的柔性件。

3.2 柔性件的设计与计算

在工件台中，y向电机1和y向电机2的不同步运动会产生附加力和力矩，为消除或降低该附加力和力矩对侧向气浮垫气膜厚度和刚度的影响，在侧向气浮垫和y向电机1之间设计Rz复合柔性件进行连接，如图4所示，其中A点和B点为气浮固定点，假设附加力和力矩作用在O'，分别为 Fo'x'，Fo'y'，Mo'z'。

图4 工件台Rz复合柔性件

3.2.1 柔性铰链的分析

在对图4中的柔性铰链组分析之前，首先对图5所示的柔性铰链1进行分析，计算铰链O点的变形量与O点施加的力的关系。

图5 柔性铰链1

由于柔性铰链1中，旋转点O1点和O2的在力作用下的变形量是叠加的效果，因此，分别通过求解Fox，Foy，Moz对旋转点O1点和O2作用时O点的变形量，再将变形量叠加可得到该复合柔性铰链力矩阵与变形量矩阵的关系。力在对复杂柔性铰链Rz柔性件分析之前，首先对简单复合柔性铰链1进行分析，计算铰链O点的变形量与O点施加力的关系为叙述方便，本文中，将称为刚度矩阵。

同时，有x向和y向的线性变形量产生，x向和y向的线性变形量和线性刚度分别为：

图6 Fox对柔性铰链O1影响示意图

同时，有x向和y向的线性变形量产生，x向和y向的线性变形量和线性刚度分别为：

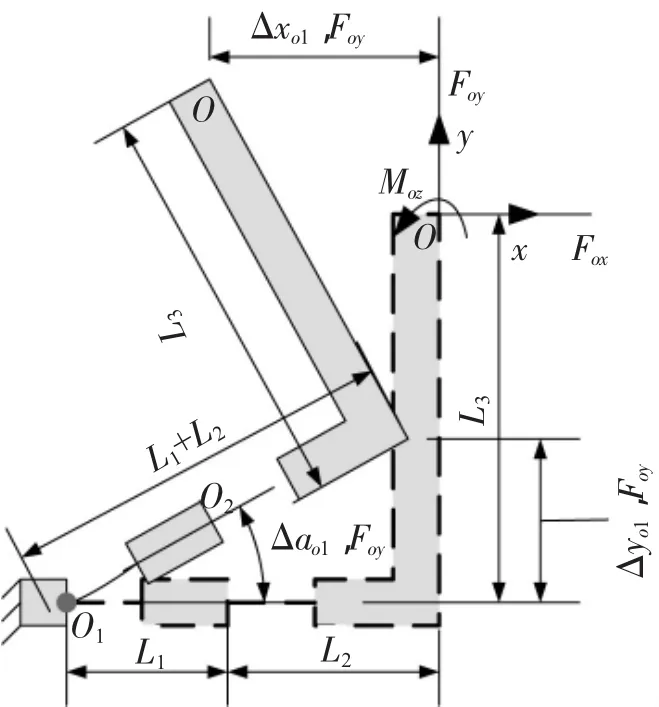
图7 Foy对柔性铰链O1影响示意图

同时，有x向和y向的线性变形量产生，x向和y向的线性变形量和线性刚度分别为：

因此，O点相对于铰链O1的刚度矩阵为：

图8 Moz对柔性铰链O1影响示意图

柔性铰链O1引起的O点的位移矩阵为：

同理，O点相对于铰链O2的刚度矩阵为：

柔性铰链O2引起的O点的位移矩阵为：

通过将O点对旋转点O1点和O2的刚度矩阵叠加，得到柔性铰链1中，O点的刚度矩阵为：

同样，当柔性铰链的结构形式如图9所示时，可求得其刚度矩阵为：

图9 柔性铰链2

3.2.2 计算与仿真

当柔性铰链的几何和材料特性如表1所示时，所求得的柔性铰链1和柔性铰链2的刚度矩阵见表2。

表1 柔性铰链的几何和材料特性

表2 柔性铰链1和柔性铰链2的刚度矩阵

当[FoxFoyMoz]=[0 5 2]时，

计算可得 [△Xo2△Yo2△γo2]计算=[1.676E-30.986E-32.18E-2]

图10为对柔性铰链2的有限元仿真分析结果图，根据仿真分析：[△Xo2△Yo2△γo2]仿真=[1.623E-30.941E-32.0E-2]，则计算结果与仿真分析结果的误差在10%以内，则该计算结果可信。因此，可用该方法对图3中Rz柔性铰链组进行分析。

图10 柔性铰链2仿真分析结果

3.3 Rz柔性铰链组分析

取图3中的Rz柔性铰链组1进行分析，如图11、图12、图13 所示。

图11 Rz柔性铰链Ⅰ

根据坐标系变换理论，求解在力Fo'x'、Fo'y'和转矩Mo'z'的作用下柔性铰链O'点的刚度矩阵。

因为，[△Xo'1△Yo'1△γo'1]T=×[△Xo1△Yo1△γo1]T[FoxFoyMoz]T=×[Fo'xFo'yMo'z]T

故Rz柔性铰链组Ⅰ的刚度矩阵为

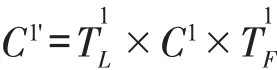
同样可求得Rz柔性铰链Ⅱ的刚度矩阵为

当Rz柔性铰链Ⅰ和Rz柔性铰链Ⅱ综合作用下，Rz柔性铰链的组合刚度矩阵为

图12 Rz柔性铰链组Ⅱ

图13 Rz柔性铰链

4 结 论

本文比较了工件台结构设计中刚性结构设计和柔性结构设计技术，提出了柔性结构设计技术在工件台设计中的重要性。文中列举了柔性结构设计中常用的柔性件的结构形式，并对常用的柔性件结构进行计算和仿真分析，通过计算结果与仿真分析结果的比较，误差在接受范围内。因此，在今后复杂柔性件的形状求解中，可根据已知刚度需求进行柔性件形状设计。

[1]于志远，姚晓先，宋晓东.基于柔性铰链的微位移放大机构设计[J].仪器仪表学报.2009，30（9）：1818-1822

[2]WU Y F，ZHOU ZH Y.Design calculations for flexure hinge[J].Review of Scientific Instruments，2002，73：3101-3106