某雷达数字化调平平台建模及算法
姜 洋,郑志军,王克军
(北方雷达电子科技集团有限公司总体一部,陕西西安 710100)
陆基雷达工作时,其工作平台通常需要手动或电动调水平,以保证雷达波束扫描时其高低指向不随方位扫描方向的变化而变化,使雷达探测空域在各个方位的方向上保持一致。但手动或电动调水平不仅会增加雷达的生产成本,而且增加了雷达架设和撤收的动作和时间。特别是对于有些特殊载车底盘雷达来说,如履带式装甲车和轮式装甲车,由于载车上没有安装调平支撑机构的合适地方,无法安装雷达调平支撑机构;同时载车底盘又非常重,因此要对载车进行调平较困难。
提出一种新型雷达数字平台调平装置及调平方法。该调平装置不直接调整雷达工作平台,而是利用姿态角传感系统上报到终端计算机的数据,通过坐标变换建立雷达数字平台,然后调整天线横轴姿态,通过这种调平方法实现雷达调平。新型雷达数字平台调平装置及调平方法克服了现有的雷达调平的不足,具有调平精度高、稳定性好、调平范围大、不受地理位置限制和雷达载车底盘限制、通用性强、可靠性高、操作简单等优点。
1 建立数学模型
图1为雷达数字平台调平方法数学模型图。雷达数字平台调平方法是利用姿态角传感系统得到当前车体的横倾角α、纵倾角β以及姿态角传感系统纵倾基准轴与北向的夹角γ,通过天线驱动控制系统得到天线方位码盘值λ,通过数据计算出方位码盘0位的方位角δ和方位码盘0位的倾角Ψ,形成初始标定参数。雷达工作时,当雷达需工作在方位角A、俯仰角E时,终端计算机依据初始标定参数计算出雷达工作时的天线方位码盘值A1、天线俯仰码盘值E1和使天线阵面直角坐标系中的X轴与水平面平行的横滚角η,建立雷达数字平台,将A1、E1发送到天线驱动控制系统,天线驱动控制系统驱动天线方位、俯仰到指定位置,然后将横滚角η发送到天线调平机构,天线调平机构驱动天线到指定的横滚角η位置,从而实现雷达工作在指定的方位角A和俯仰角E上,同时也保证了天线阵面直角坐标系中X轴与水平面平行,从而使雷达波束在各个方位扫描方向上的高低角保持不变,实现了对雷达调平功能。
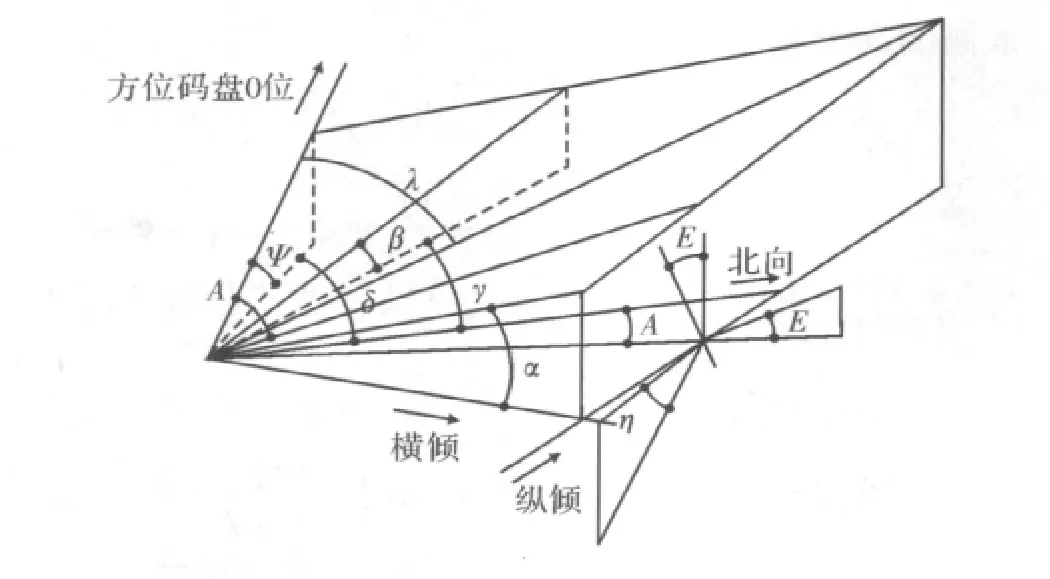
图1 数学模型图
由图1可以看出,数学模型复杂,必须进行分解,使复杂问题简单化。总结以上图形特征,可将整个数学模型分解为以下几种简单模型进行分析。
1.1 数学模型1
在已知横倾a、纵倾b及一条直线L与纵倾的夹角为c时,求解直线L的倾角d。如图2所示,矩形OABC共面,设为Σ,OMPQ为水平面Π,CQ⊥Π,AM⊥Π,BP⊥Π,CH∥PQ,OA⊥OC。∠AOM=∠BCH=b,∠COQ=a,∠AOB=c,∠BOP=d,则
d=arcsin(sinc·sina+cosc·sinb) (1)

图2 数学模型1几何示意图
1.2 数学模型2
已知直线L的倾角为a,直线M的倾角为b,直线L与M的夹角为c∈[0,π],求解L与M在水平面投影的夹角d。如图 3所示,∠AOC=a,∠BOD=b,∠AOB=a,∠COD=d,则
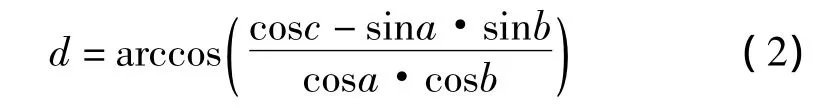
1.3 数学模型3
已知横倾角为a,纵倾角为b,求纵倾轴绕横倾轴旋转到水平面的旋转角d。如图4所示,∠COD=a,∠AOE=b,∠AOB=d,则

同理,可得横倾轴绕纵倾轴旋转到水平面的旋转角
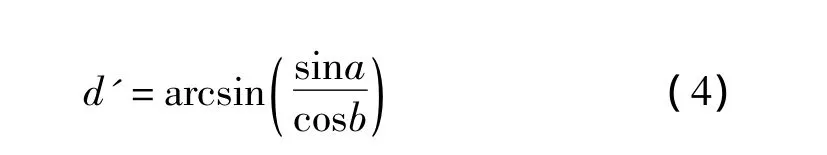

1.4 三维坐标旋转公式
在O-XYZ坐标系中,绕OX旋转α,再绕OY轴旋转β,最后绕OZ轴旋转γ后的坐标旋转公式[1]如下
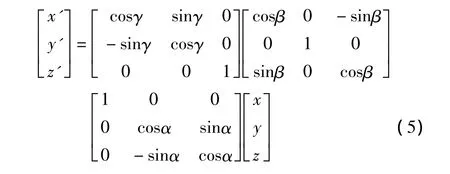
2 方位标定
雷达工作的首要任务是进行标定,即标定方位码盘零位与正北的夹角。设寻北仪的纵倾基准轴在水平面上的投影与北向的夹角为寻北角,设方位码盘零位时,纵倾基准轴与码盘零位的夹角为ε。当方位码盘值为λ时进行寻北,得到横倾角为α,纵倾角为β和寻北角γ。此时纵倾基准轴与码盘零位的夹角为ε+λ,设 μ= -(ε+λ)。
依据式(1)可得到此时码盘零位的倾角

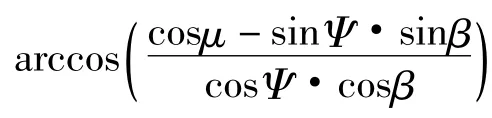
3 方位、俯仰码盘值转换为方位角、俯仰角
3.1 方位码盘值对方位角的影响
当方位码盘旋转到φ角度时,方位码盘值所对应直线北的夹角为Γ。
φ为方位码盘值所对应直线N与方位码盘零位的夹角,寻北时纵倾基准轴与方位码盘零位的为夹角ε+λ,则N纵倾基准轴与的夹角为ρ=φ-λ-ε=φ+μ,设N的倾角为 χ,根据式(1)可得 χ=arcsin(sinρ·sinα +cosρ·sinβ)。

3.2 俯仰码盘的高低角和对方位角的影响
天线绕俯仰轴旋转θ时,求天线阵面法线的高低角和方位角误差。
由于俯仰旋转轴与方位码盘值所对应直线垂直,因此以俯仰旋转轴为X轴,以码盘所对应直线为Y轴建立右手坐标系。
俯仰旋转轴与寻北时纵倾基准轴的夹角为ρ+π/2。根据式(1)可得俯仰旋转轴在水平面上的倾角κ=arcsin(cosρ·sinα -sinρ·sinβ)。
接下来的求解可用坐标变换解决,设天线绕俯仰旋转轴旋转θ时,在天线阵面法线上取点P(0,1,0),经过一系列的坐标旋转将X-Y-Z旋转到水平坐标系,并且要求旋转后的水平坐标系的Y2轴须与Y轴在水平面的投影重合。坐标旋转过程如下:
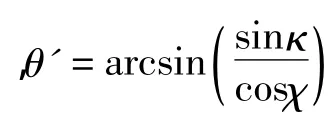
(- sinθ'·sinθ,cosχ·cosθ- sinχ·cosθ'·sinθ,sinχ·cosθ+cosχ·cosθ'sinθ),从而可以计算P'点在水平面的高低角和方位角误差。
其中,x= - sinθ'·sinθ;y=cosχ·cosθ- sinχ·cosθ'·sinθ。高低角为∏ =arcsin(sinχ·cosθ+cosχ·cosθ'sinθ)。
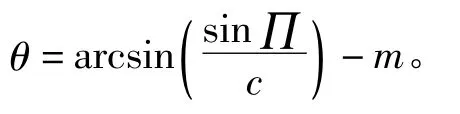
3.3 天线阵面的方位角和高低角
结合上文可得到,当方位码盘值为A1,俯仰码盘值E1时,天线阵面的方位角A和俯仰角E分别为A=Γ +Δ;E=∏。
4 使天线旋转到指定位置且调平
4.1 计算方位与俯仰码盘值
为使天线的方位角为Λ,俯仰角为Π,求得方位码盘值φ和俯仰码盘值θ。
当方位码盘值为 φ时,设 ρ=φ-λ-ε,根据式(1),φ对应直线的倾角为 χ=arcsin(sinρ·sinα+cosρ·sinβ)。俯仰旋转轴的倾角为 κ =arcsin(cosρ·sinα -sinρ·sinβ)。

求解该方程很复杂,为了在计算机中应用,可采用迭代法,迭代过程如下:当方位码盘值φ时,可得到Γ,当俯仰角为Π时,可求解到θ和Δ,令A^=Γ+Δ,当A^与Λ的误差小于一定精度时,即得到φ和θ。
4.2 计算横滚角,实现调平
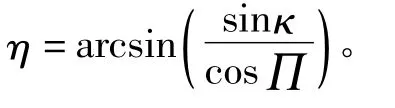
5 结束语
算法化简了问题的复杂性,使得复杂的坐标变换问题,变为几个简单的立体几何问题,且有利于计算机编程实现,现成功应用于某相控阵雷达。
[1]同济大学大地测量教研室,武汉测绘科技大学控制测量教研室.控制测量学:下册[M].北京:测绘出版社,1995.
[2]彭雪梅,张军.微波着陆系统信号的模拟与应用[J].电子科技,2010,23(2):53 -55.
[3]许杰田,张猛,李杰,等.基于矢量有限元法的微波谐振腔高频特性研究[J].电子科技,2010,23(10):63 -65.
[4]祁云飞.基于小信号S参数的功率放大器设计[J].电子科技,2010,23(8):72 -73,76.

