饱和软土的经验型蠕变模型

张先伟，王常明

(吉林大学 建设工程学院，吉林 长春，130026)

软土广泛分布于我国东南沿海、内陆湖泊地区，由于特殊的沉积环境，软土物质成分复杂，含水量高，多呈絮凝状结构，从而表现出与一般黏性土不同的力学效应，如低强度和蠕变性等。研究表明：软土蠕变性呈现较强非线性特性，即软土的应力-应变不仅与时间有关，还与当时的应力水平有关[1-2]。目前，对于土体的弹塑性变形行为，已经有比较成熟的模型和理论模型描述，而对于同时存在弹塑性剪切变形和剪切蠕变变形的过程(也称为黏弹塑性变形过程)如何进行合理描述研究较少[3]。一般描述这种过程多采用模型理论或经验理论。著名的模型理论有Maxwell模型、Kelvin模型和Burgers模型，这些模型概念直观、物理意义明确，但要准确模拟土的黏弹塑性需要引入很多的元件进行组合，模型参数数量多，给工程应用带来不便[4]。经验型模型是根据土体的试验结果总结本构关系，其优势在于只用少量的参数就能达到较好的拟合效果，所以，在工程实践中具有一定的应用价值，如Buisman半对数形式蠕变方程和孙钧[5]提出的上海软土蠕变经验模型，以及Bjerrum提出瞬时压密和迟滞压密的概念并建立的一维蠕变模型。但是由于一维固结蠕变试验的加荷路径是一种特殊的等有效应力比路径即K0路径，在这种受力条件下，固结占据主导地位，蠕变特性不能充分发挥，从而表现出蠕变速率随着软土蠕变程度的增加而减小[6]。为了更充分揭示软土的蠕变规律，许多学者选择了三轴蠕变试验，得到了很多经典的经验蠕变模型，如Singh-Mitchell模型、Mesri模型，国内外不少学者针对这 2种经验蠕变模型开展了软土蠕变特性的研究[6]。本文作者对漳州地区饱和软土在围压为100 kPa条件下，开展不同应力加载等级下的三轴固结排水与固结不排水蠕变试验，在总结经验模型 Singh-Mitchell模型和 Mesri 模型的基础上，提出一种新的经验型蠕变模型。由试验结果对比分析可知，该蠕变方程能较好地反映和预测饱和软土的蠕变特性。

1 软土三轴蠕变特性

1.1 土样基本性质与试验方案

试验土样为漳州市九龙江出海口南岸深 12～20 m，属于第四系全新世深灰色海陆交互相软土，其物理力学性质见表1。从表1可见：漳州软土具有典型软土特征，表现为高含水率、大孔隙比、强度指标低和高压缩性等。

目前，实验室所用的三轴仪多为应变控制式，而蠕变试验要求保持恒定的应力下能观察应变与时间的关系，因此，应变式三轴仪不能满足蠕变试验要求。本次试验所用仪器是在SJ-1A G应变控制式三轴仪基础上改装加载系统而成，即在土样轴向改装成横梁式加压系统，使之能在轴向保持恒力；在加压杆上安装百分表用以测定土样的变形。三轴蠕变试验分为排水与不排水2组，围压均取100 kPa，采用分级加载方式。试验过程如下：(1) 通过常规三轴试验获取土样在排水与不排水条件下的破坏应力 Dmax=(σ1-σ3)f，其中σ1为最大主应力)；(2) 施加围压σ3直至试样固结；(3)将固结完成后测得的各读数作为三轴蠕变试验初始读数，然后施加偏应力D，D=Dmax/m，在排水条件下，m 为 5～7，在不排水条件下，m=8～10；(4) 采用分级加载的试验方法，观测轴向变形及体积变形随时间的变化过程，当变形速率小于0.01 mm/d时施加下一级荷载；(5) 当变形稳定后再施加下一级荷载，如此反复，直至土样破坏或达到一定的变形值为止。

1.2 试验数据结果与分析

图1所示为饱和软土在排水与不排水条件下不同偏应力q的蠕变曲线。由图1可见：轴向应变与时间的关系在ln ε-ln t关系坐标系中呈现良好的线性关系，并且不同偏应力下的ln ε-ln t关系几乎是相平行的直线，只是当偏应力较小时，直线的斜率n稍大。关于较低剪应力水平下存在较大n解释是：n受土固结状态影响较大，最重要的变化是n随着超固结比增大而减小[5]。作者认为引起这种现象的主要原因是：土样在受压开始阶段，颗粒重新排列以及剪切阻力的黏滞性对土样的蠕变特性影响较大，随着时间的延长，土内部颗粒排列趋于稳定，n将趋于稳定。

图2所示为饱和软土在排水与不排水条件下的应力-应变等时曲线。对比图2(a)与图2(b)可知：软土黏塑性与排水条件密切相关；在排水条件下，软土的黏塑性并不明显，无明显的屈服点，可以近似看作是非线性黏弹性体(图2(a))；在不排水条件下，等时曲线形态均不是直线，而是一簇相似的曲线，说明软土蠕变具有非线性[7-8]。软土在极小应变下就产生明显黏塑性，屈服应力约为 50 kPa，可看作黏弹-黏塑性体，因此，软土蠕变模型应为非线性模型。对这些等时曲线进行归一化处理，发现应力-应变等时曲线可以用双曲线函数来描述。

表1 漳州软土物理力学性能Table1 Physical and mechanical properties of Zhangzhou soft soils

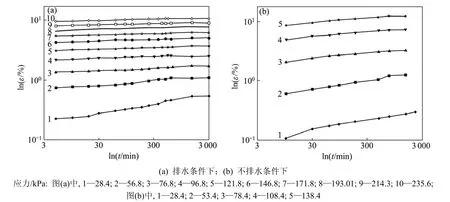
图1 100 kPa围压下饱和软土蠕变曲线Fig.1 Creep curves of saturated soft soil under 100 kPa

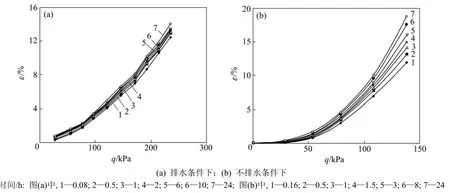
图2 100 kPa围压下饱和软土等时曲线Fig.2 Creep equal-time curves of saturated soft soil under 100 kPa

2 软土三轴蠕变特性

在三轴不排水蠕变试验中，土样在各级偏应力作用下均没有固结排水的过程，随着时间的延长产生变形，这是蠕变造成的；而对于三轴排水蠕变试验，土样的变形是主固结与次固结共同产生的，其中次固结根据时间先后又可分为准蠕变和蠕变，而蠕变则发生在主固结完成之后，在有效应力稳定的条件下使得土体变形随着时间不断发展。

两者的变形机理相同，但土体的受力情况却完全不同[9]。因此，能描述不排水蠕变的模型并不一定适用于排水蠕变。目前，能描述2种蠕变情况且应用广泛的经验型模型主要有 Singh-Mitchell模型和 Mesri模型[10-12]。

Singh和mitchell根据单级加载的排水与不排水三轴压缩蠕变试验，提出了一个应力-应变-时间关系模型，其应力-应变关系采用指数函数，应变-时间关系采用幂次形式[13]。Kondner提出应力-应变关系采用双曲线形式，进而得到Mesri模型[14-15]。这2个模型都具有参数少和适用性强的特点。但 Singh-Mitchell模型仅适合描述剪切应力水平在 20%～80%范围内的应力-应变关系，例如，当剪切应力水平为 0时却预测有非零的应变[11]。Mesri模型虽然能模拟全部应力水平状态，但对于蠕变特性不强、蠕变应变速率较小的软土，得到的模型曲线应变速率比试验值增长较快，这种现象在高应力水平下尤为突出[6]。

通过本文的蠕变试验研究，建议应力-应变关系采用双曲线形式，对 Singh-Mitchell模型进行改进，得到下式：

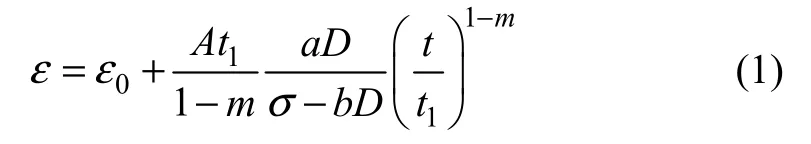
上述的饱和软土经验型模型只有C，b和n这3个参数，参数C和b反映土的蠕变速率的数量级，从某种意义上反映土的组成、结构和应力历史对变形与强度的影响[16]；参数n 表现为应变速率随着时间减小的速度。在Singh-Mitchell方程和Mesri方程中，为了取得模型参数中的剪应力水平值需要进行额外的三轴剪切试验，这无疑使模型的适用性大大降低。而本文所提出的经验型蠕变模型，只需要给出一组蠕变数据，模型参数就可以通过2组关系图中全部获得。式(4)中的参数C和b可从t=t1时的 (σε/ D ) -ε关系中得到，C为拟合直线的截距，b为拟合直线的斜率；参数 n即为蠕变曲线ln ε-ln t中直线的斜率。参考时间t1可以取任意值，但不影响模型参数值，本文取t1=1 h，得到饱和软土在不同排水条件及各级偏应力下的 n，见表2。

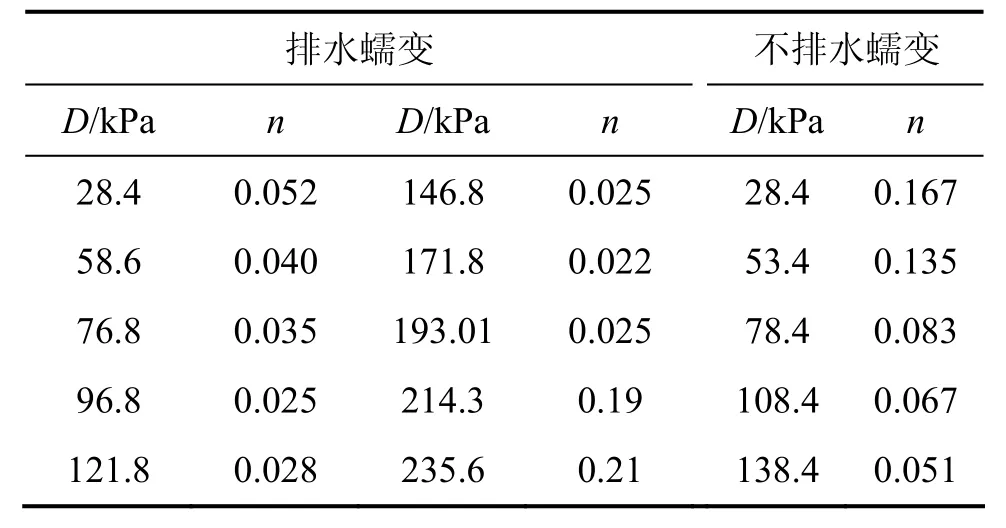
表2 饱和软土不同应力差下的nTable2 n for saturated soft soil in different stresses

饱和软土蠕变模型中参数C和b可以从图3中获取。n为蠕变曲线在双对数坐标中的拟合直线的斜率，在不同应力差下，其直线斜率相似，可以取其平均值作为模型中的 n。用相同方法可得到饱和软土不同围压下的蠕变模型。

对排水蠕变：

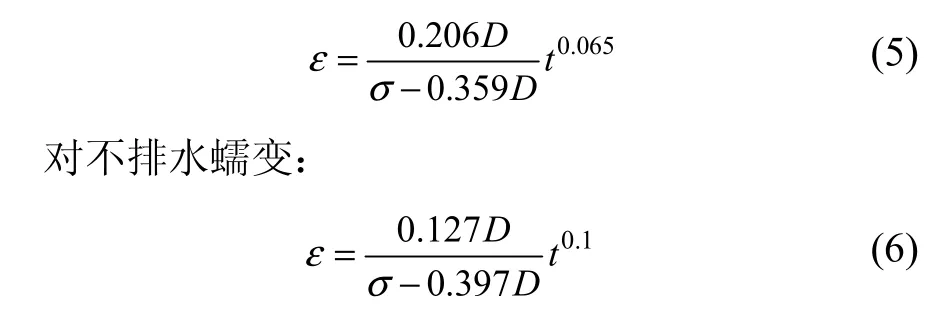
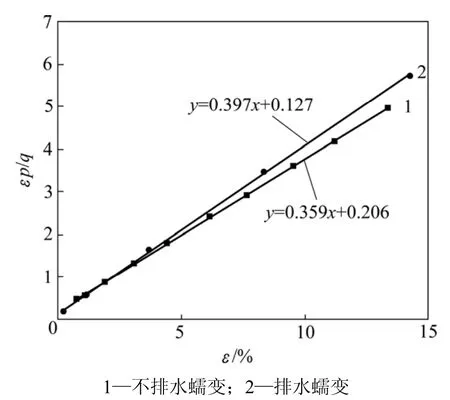
图3 归一化应力-应变关系(t1=1 h)Fig.3 Normalized stress-strain relations of saturated soft soils

3 饱和软土经验型蠕变模型的验证

采用 Singh-mitchell模型和 Mesri 模型对三轴蠕变试验数据进行拟合，拟合精确度较低，说明这2个经验型蠕变模型并不完全适合本文试验数据。图4所示为本试验数据与 Singh-mitchell模型计算结果对比图，可见：在偏应力较高时，拟合曲线数据点差异较大。这主要是因为幂函数形式的应力-时间关系不是衰减的，无法描述衰减蠕变逐渐趋于稳定的特性，且该模型只适用于工程常见的应力水平范围，当偏应力水平大于80%或者小于20%时，计算值误差增大。通过Mesri模型进行拟合也出现类似的问题(图5)。

利用式(5)和(6)对试验数据进行拟合(图 6)，对三轴固结排水与不排水蠕变试验数据的拟合结果较好，在不排水条件及偏应力为138.4 kPa作用下的数据拟合相关系数R2=0.965，其他偏应力条件下的数据拟合相关系数R2可达0.98以上。可见：无论排水情况还是不排水情况，模型所得计算曲线与试验曲线都趋于一致，尤其在高应力状态下，对蠕变后期的预测效果要远远比Singh-Mitchell 模型和Mesri 模型的预测效果好。只是不排水蠕变下的某些点拟合略差一些，分析原因主要是：在不排水蠕变试验过程中，读取土样受压下的变形值的时间间隔较大，导致每一级偏应力下试验数据点较少，通过这些数据点去拟合时精度降低，进而导致获取的模型参数有较小误差。解决这问题的方法就是减小读数的间隔，获取更多的数据点。

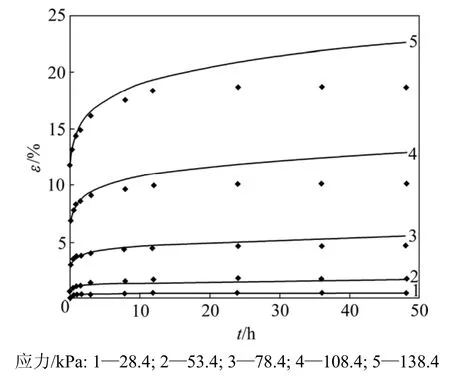
图4 试验数据与Singh-Mitchell模型计算结果比较Fig.4 Comparisons between test data and calculated results using Singh-Mitchell’s model

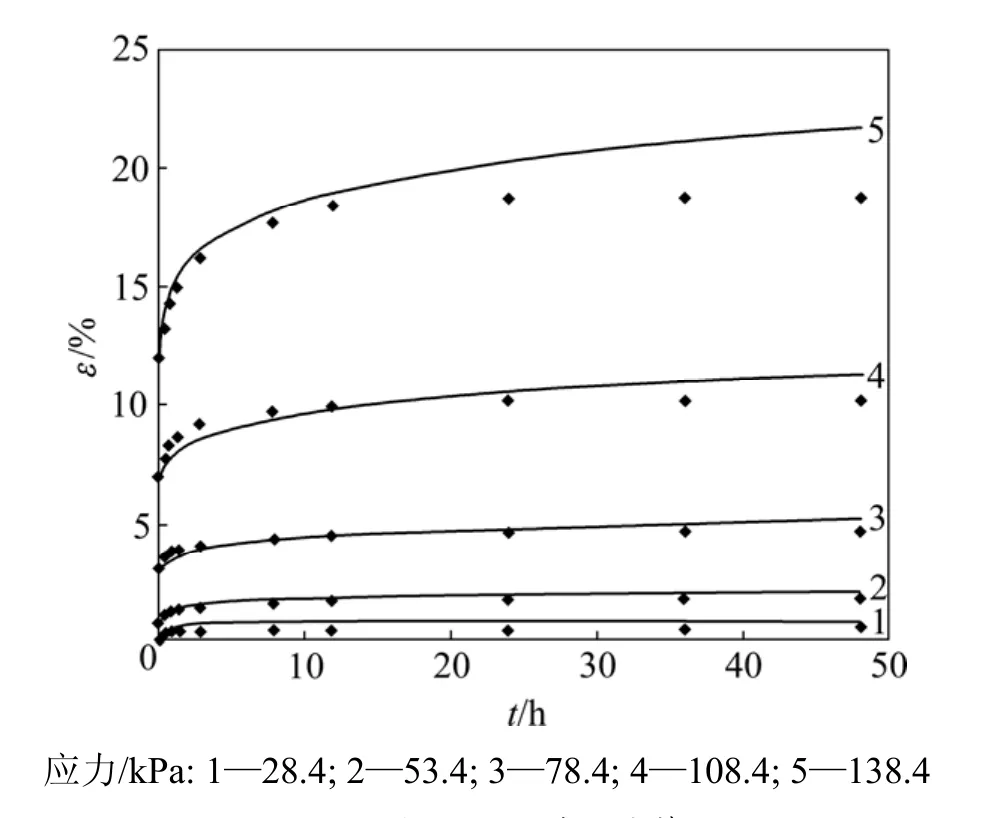
图5 试验数据与Mesri模型计算结果比较Fig.5 Comparisons between test data and calculated results using Mesri’s model

此外，从图1和表2可见：不同偏应力下的ln εln t的关系图中拟合直线的斜率n是不同的，一般剪应力较小时n较大；n随偏应力增大而降低。本文建议可以取拟合直线斜率的平均值作为模型中的 n，但是，对于n随偏应力变化较大时，这种方法会降低模型的精度。为解决此问题，可通过对n进行分段求平均值的方法。例如式(6)也可以改为：

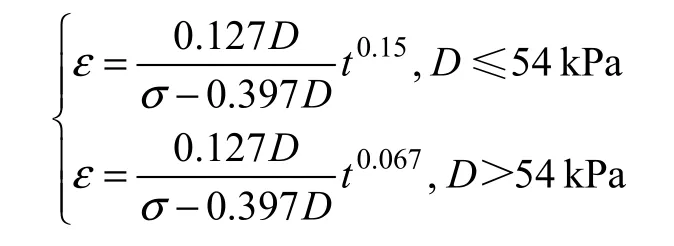
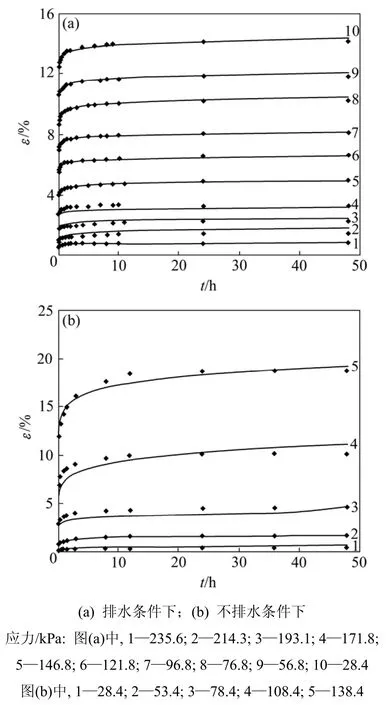
图6 经验型蠕变模型计算曲线与试验曲线比较Fig.6 Comparisons between test data and calculated results using empirical creep equation

4 结论

(1) 软土具有非线性蠕变的特性。Singh-Mitchell模型和Mesri 模型对同一围压下的蠕变曲线拟合效果较差，这在应力水平较高时尤为突出。Singh-Mitchell模型和Mesri 模型并不完全适合于描述三轴剪切蠕变性状。

(2) 将应力-应变关系用一双曲线函数来描述，得到1个新的经验型蠕变模型。该模型能描述不同应力水平下的应力-应变-时间关系，模型参数只有3个，且容易确定。

(3) 新建蠕变模型计算的结果与不排水和排水蠕变试验数据拟合精度较高，表明新建蠕变模型可以较好地描述不排水和排水条件下的蠕变性状。

[1] 张先伟, 王常明, 王钢城, 等. 黄石淤泥质土的剪切蠕变特性及模型研究[J]. 吉林大学学报: 地球科学版, 2009, 39(1):119-125.

ZHANG Xian-wei, WANG Chang-ming, WANG Gang-cheng, et al. Study on shearing creep characteristics and constitutive model of Huangshi mucky soil[J]. Journal of Jilin University: Earth Science Edition, 2009, 39(1): 119-125.

[2] 王彬, 王常明, 张先伟, 等. 漳州软土蠕变特性的试验研究[J].工程地质学报, 2008, 16(增刊): 645-649.

WANG Bin, WANG Chang-ming, ZHANG Xian-wei, et al.Experimental research on creep characteristics of Zhangzhou soft soil[J]. Journal of Engineering Geology, 2008, 16(Suppl):645-649.

[3] 王常明. 土流变学研究现状与趋势[J]. 世界地质, 1998, 17(4):33-37.

WANG Chang-ming. Current situation and tendency of soil rheology[J]. Global Geology, 1998, 17(4): 33-37.

[4] 袁静, 龚晓南, 益德清. 岩土流变模型的比较研究[J]. 岩石力学与工程学报, 2001, 20(6): 772-779.

YUAN Jing, GONG Xiao-nan, YI De-qing. Comparison of rheological constitutive model[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 772-779.

[5] 孙钧. 岩土材料流变及工程应用[M]. 北京: 建筑工业出版社,1999: 113-119.

SUN Jun. Rheology and application of geotechnical materials[M]. Beijing: China Architecture & Building Press,1999: 113-119.

[6] 卢萍珍, 曾静, 盛谦. 软黏土蠕变试验及其经验模型研究[J].岩土力学, 2008, 29(4): 1041-1044.

LU Ping-zhen, ZENG Jing, SHENG Qian. Creep tests on soft clay and its empirical models[J]. Rock and Soil Mechanics, 2008,29(4): 1041-1044.

[7] 侍倩. 饱和软黏土蠕变特性试验研究[J]. 土工基础, 1998,12(3): 40-44.

SHI Qian. Experimental investigation of creep behaviour of saturated soft clay[J]. Soil Engineering and Foundation, 1998,12(3): 40-44.

[8] 韩爱果, 聂德新, 任光明, 等. 大型滑坡滑带土剪切流变特性研究[J]. 工程地质学报, 2001, 9(4): 345-348.

HAN Ai-guo, NIE De-xin, REN Guang-ming, et al. Study on shear rheologic behaviors of soil in slip zone of large-scale landslide[J]. Journal of Engineering Geology, 2001, 9(4):345-348.

[9] 朱鸿鹄, 陈晓平, 程小俊, 等. 考虑排水条件的软土蠕变特性及模型研究[J]. 岩土力学, 2006, 27(5): 694-698.

ZHU Hong-hu, CHEN Xiao-ping, CHENG Xiao-jun, et al. Study on creep characteristics and model of soft soil considering drainage condition[J]. Rock and Soil Mechanics, 2006, 27(5):694-698.

[10] 李军世, 孙钧. 上海淤泥质黏土的 Mesri 蠕变模型[J]. 土木工程学报, 2001, 34(6): 74-79.

LI Jun-shi, SUN Jun. Mesri’s creep model for Shanghai silt-clay[J]. China Civil Engineering Journal, 2001, 34(6):74-79.

[11] 王琛, 张永丽, 刘浩吾. 三峡泄滩滑坡滑动带土的改进Singh-Mitchell蠕变方程[J]. 岩土力学, 2005, 26(3): 415-418.

WANG Chen, ZHANG Yong-li, LIU Hao-wu. A modified Singh-Mitchell’s creep function of sliding zone soils of Xietan landslide in Three Gorges[J]. Rock and Soil Mechanics, 2005,26(3): 415-418.

[12] 王琛, 刘浩吾, 许强. 三峡泄滩滑坡滑动带土的改进 Mesri蠕变模型[J]. 西南交通大学学报, 2004, 39(1): 15-19.

WANG Chen, LIU Hao-wu, XU Qiang. Modified Mesri’screep model for soils in sliding zone of Xietan landslide in Three Gorges[J]. Journal of Southwest Jiaotong University, 2004, 39(1):15-19.

[13] Singh A, Mitchell J K. General stress-strain-time function for soils[J]. Journal of Soil Mechanics and Found Engineering Division, ASCE, 1968, 94(1): 21-46.

[14] Kondner R L. Hyperbolic stress-strain response: cohesive soils[J]. Journal of Soil Mechanics and Foundation Engineering ASCE, 1963, 89(1): 115-143.

[15] Mesri G, Rebres-Cordero E, Shields D R, et al. Shear stress-strain-time behaviour of clays[J]. Geotechnique, 1981,31(4): 537-552.

[16] 王常明, 王清, 张淑华. 滨海软土蠕变特性及蠕变模型[J]. 岩石力学与工程学报, 2004, 23(2): 227-230.

WANG Chang-ming, WANG Qing, ZHANG Shu-hua. Creep characteristics and creep model of marine soft soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2):227-230.