基于多频约束和解析灵敏度法的大型振动筛优化设计

贺孝梅，刘初升，张成勇

(1. 中国矿业大学 艺术与设计学院，江苏 徐州，221116；2. 中国矿业大学 机电工程学院，江苏 徐州，221116；3. 中国矿业大学 化工学院，江苏 徐州，221116)

大型振动筛在工作过程中，侧板分布着很大的惯性力，筛体做刚体运动的同时也在做弹性变形运动，使得侧板产生较大的动应力[1]，容易形成疲劳裂纹从而导致振动筛损坏。要提高振动筛的可靠性，就需要解决侧板振动过程中应力过高的问题。机械机构中加筋板是控制基体结构应力水平的一种常见而有效的方法[2]，但筋板的结构尺寸及其在基体材料上的布置问题一直是侧板结构设计的一个难点问题。加强筋的位置、尺寸及厚度一般都是根据工程技术人员的经验设计的，缺乏理论依据。现有的文献[3-5]对于振动筛的优化设计，大多是从工艺参数及物料运动特性如筛面长度、倾角、筛孔尺寸、抛掷指数和物料运动轨迹等方面进行研究，对于结构的位置和形状尺寸优化方面的研究较少。为了解决大型振动筛工作过程中侧板动应力过高、易损坏的问题，有必要研究筛体侧板加强筋的结构尺寸及位置布置。为此，本文作者研究基于多频约束和解析灵敏度分析法的加强筋的结构尺寸优化，给出适合多频约束求解的优化准则。

1 解析灵敏度计算方法

在对结构进行优化的过程中，需要对结构参数进行修改，应用灵敏度分析可以找出对结构系统总体动态特性影响最大的结构参数，从而使结构修改再设计工作收到事半功倍的效果。一般优化设计软件计算灵敏度时，结构优化程序基本上都采用差分法或半解析法，但根据这2种方法计算的灵敏度受差分步长的影响而不稳定，还会导致结构优化分析次数增加，使计算效率低和优化结果不明显。根据文献[6-8]中灵敏度计算方法，本文给出了目标函数和约束条件的解析灵敏度的计算公式，以结构的质量作为目标函数，以频率作为主要的约束形式，则目标函数的解析灵敏度方法为：

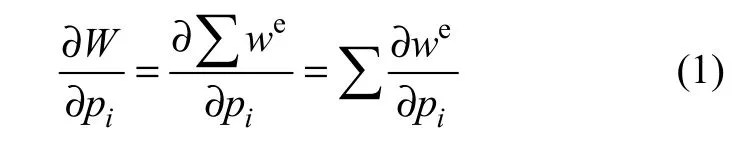
式中：W 为目标函数；we为单元的质量；pi为设计变量。

约束条件的解析灵敏度计算方法：

式中：rλ为频率约束条件；rφ为相应频率的模态；K为结构的总体刚度矩阵；M为结构的总体质量矩阵；ke为单元的刚度矩阵；me为单元的质量矩阵。

由理论分析可知：由式(2)或(3)都可以计算出约束频率的解析灵敏度。根据式(2)的计算方法，首先要组装总体刚度矩阵和总体质量矩阵对设计变量的偏导数矩阵，然后计算结构频率的灵敏度，这在程序实现上容易，但2个与总体刚度矩阵同样大小的大型矩阵的组装，会花费较多的时间，也需要较多的存储空间；并且根据结构优化的特点[8]，在绝大多数情况下，总体刚度矩阵和总体质量矩阵对设计变量的偏导数矩阵的非零元素比较多，这样，就有许多零与非零相乘的无用计算。根据式(3)，在求得相关单元的刚度矩阵和质量矩阵对设计变量的偏导数后，计算各个相关单元对频率灵敏度的贡献，并将单元的贡献叠加求和得到频率灵敏度。这样，可以节省总体刚度矩阵和质量矩阵的偏导数矩阵所占的存储空间，也省去了大型矩阵的组装、相乘运算，有利于节省存储空间，提高计算效率。

由式(3)可知：求结构频率的灵敏度时，需要计算单元刚度矩阵和质量矩阵的偏导数。将这些计算功能插入结构优化分析程序后，在结构分析的同时，就可以计算单元刚度矩阵和单元质量矩阵的偏导数矩阵。

2 振动筛优化参数的确定

2.1 振动筛侧板基本结构

振动筛侧板加强筋板尺寸的优化首先要确定基本弹性体结构。以基于超静定网梁激振结构[9]设计的大型振动筛为研究对象，根据振动筛实际结构给出了侧板的初始结构，如图1所示。在基本结构中左右2个孔为振动筛支承梁的孔，中间2个孔为振动筛激振器安装孔，其位置由振动筛的设计工艺所确定。

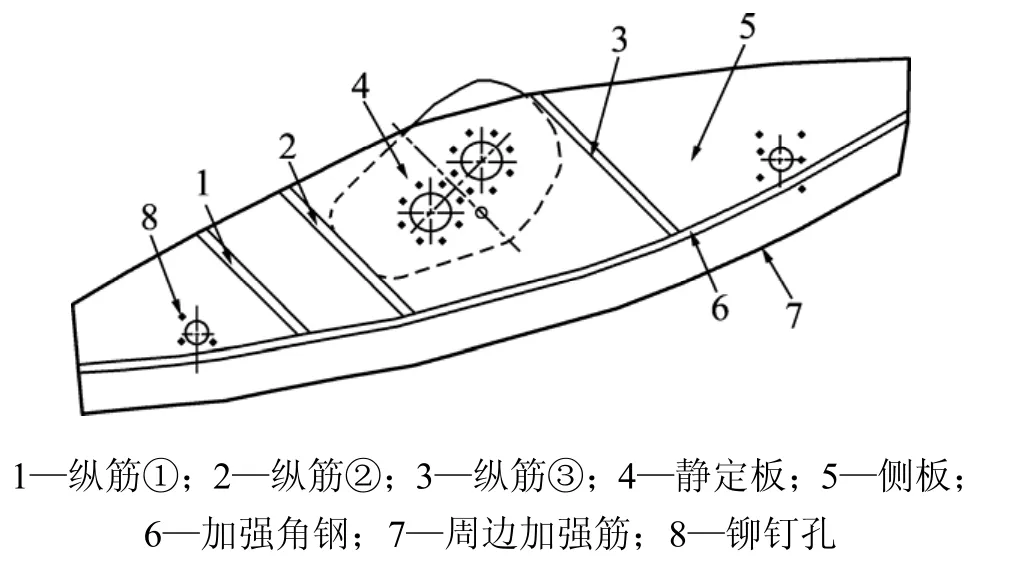
图1 振动筛侧板的初始结构Fig.1 Original structure of vibrating screen’s side plate

2.2 优化参数的确定

以质量最小为目标的频率优化问题通常可表述如下[10]。

(1) 目标函数：

式中：x为包含n个xi的矢量；ρi为密度；xi为设计变量；li为单元长度；Gj(x)为挠度、应力和频率等行为量；为需满足的限制值；和分别为单元尺寸的上限和下限。

由于侧板结构形状比较复杂，优化过程中周边加强筋与侧板接触部分的单元会因为多次的循环求解造成单元形状的畸变而中止优化程序的执行。为保证优化的效果，需要对侧板结构进行合理的简化，简化后的结构频率会有一定程度下降，这在优化过程中会加以考虑。侧板简化的结构如图2所示。

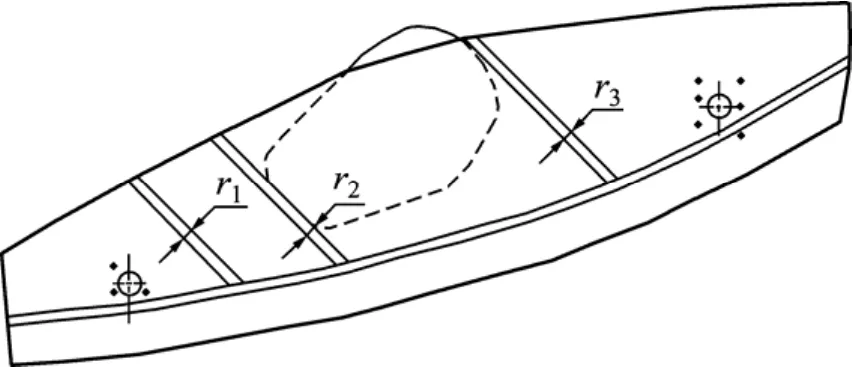
图2 侧板的简化结构Fig.2 Simplified structure of side plate

结构优化过程中，以3个纵筋的截面宽度 r1，r2和r3及筋板的厚度h作为目标函数的设计变量。设计变量初始值为：r1=100 mm，r2=100 mm，r3=100 mm，h= 100 mm。 给出设计变量的上、下限约束条件：

60≤r1≤140 mm；60≤r2≤140 mm；

60≤r3≤140 mm；60≤h≤130 mm。

为满足机械结构可靠性的要求，考虑振动筛的动态特性，以模态频率作为约束条件。由于低阶弹性模态频率与振动筛工作频率12.17 Hz比较接近，对振型的影响较大，因此，以前3阶模态频率f1，f2和f3作为约束条件。结构优化前，对振动筛侧板固有特性进行分析，得到其前 3阶模态频率分别为 4.24，15.04和17.16 Hz。由模态叠加原理和动、静应力之间关系理论及振动筛测试结果[10]可知：惯性振动筛结构的固有频率与其工作频率之差大于5 Hz，筛机才不会因共振发生早期失效。同时考虑到结构简化的影响，状态变量的上、下限约束条件为：

f1≤7.17 Hz；f2≥17.17 Hz；f3≥19.30 Hz。

优化过程以质量mt作为优化目标，通过灵敏度分析，使得结构参数在满足频率的条件下，结构质量最小，从而节省材料降低工程造价。侧板的初始质量为2.352 80 t。

3 优化准则

多频约束问题，一般可以表示为[11-12]：

式中：Ψj为第j阶特征向量。考虑到结构非线性特性，单元刚度矩阵ke和单元质量矩阵me可表示为[13-14]：

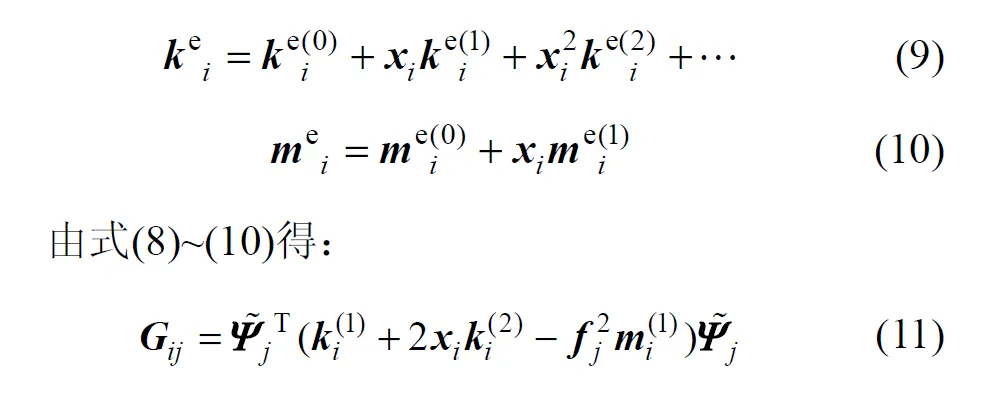
式中：Ψ ˜j为对M标准化后的模态向量。

根据优化参数构建拉格朗日方程：

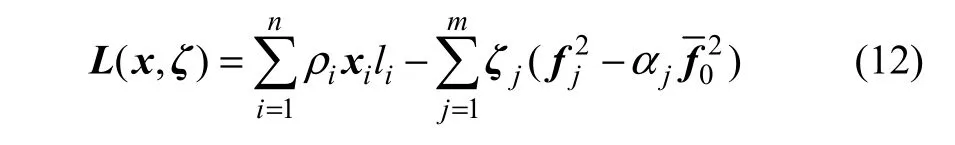
式中：ζ为拉格朗日算子。

式(11)对 xi微分求 L的最小值，则优化准则可写为：

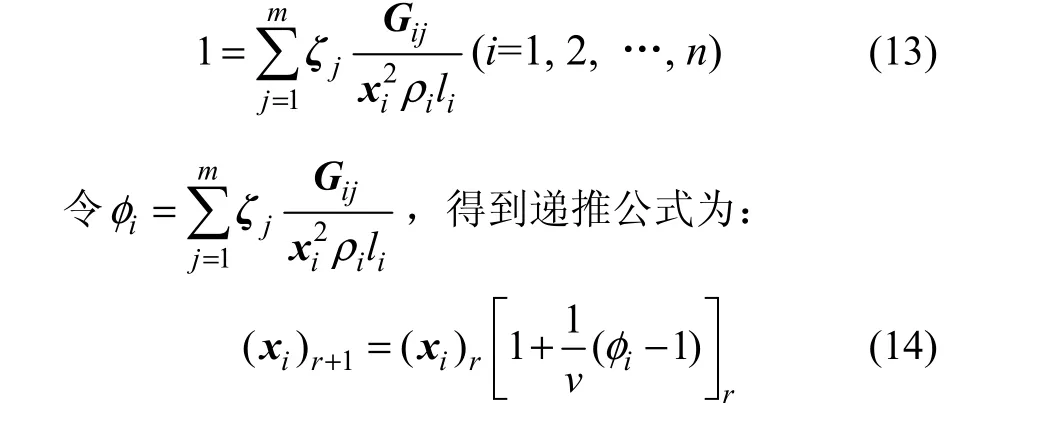
式中：r为循环数；v为步长因子。

Khot[15]给出了求ζj的等式，但是比较复杂，通过调整参数并作简化，得到1个近似的ζj，计算结果表明该值满足计算要求。

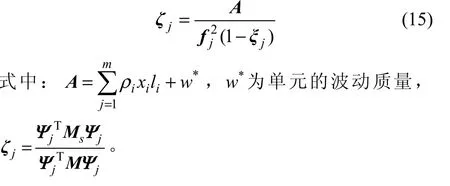
4 优化结果分析

4.1 侧板优化结果

根据推导得出的递推公式进行迭代计算，迭代12次得到优化结果，如表1所示。最优的结果是序列10，此时 r1=60.29 mm，r2=60.31 mm，r3=61.10 mm，h=60.36 mm，f1=4.17 Hz，f2=15.30 Hz，f3=17.66 Hz，mt=2.158 30 t。

在优化过程中，优化目标mt优化进程如图3所示，变量h，r1，r2和r3的优化进程如图4～7所示，约束频率f1，f2及f3优化进程如图8～10所示。

将最优的结果与优化前结果相比较，如表2所示。由表2可知：结构优化后侧板的质量降低了8.27%，达到了比较好的优化效果。第1阶模态频率为刚体运动频率，数值变小，满足工作要求；第2阶和第3阶模态频率分别提高1.73%和2.91%，与工作频率12.17 Hz相距较远，可以有效地避免共振，防止振动筛结构的损坏。

图3 mt优化进程Fig.3 Optimization process of mt

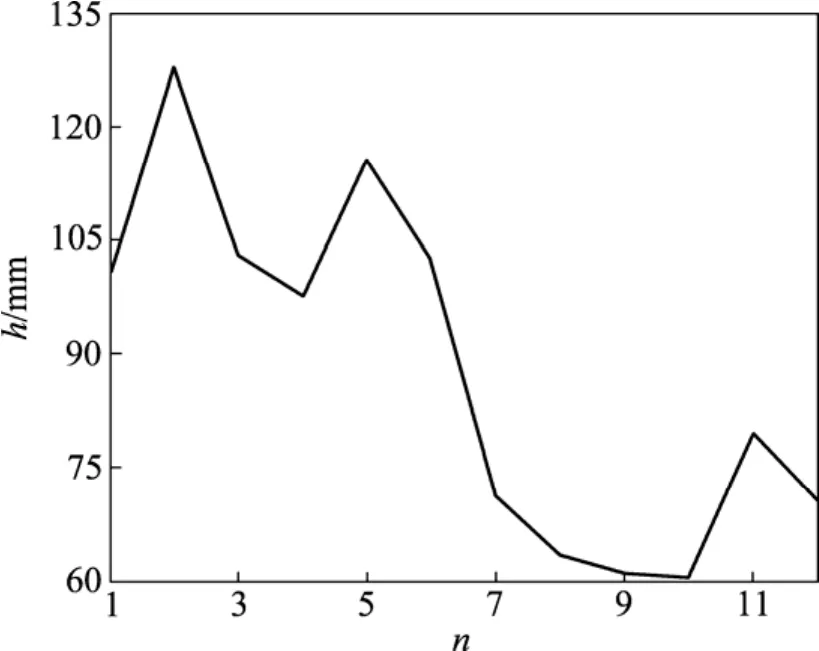
图4 h优化进程Fig.4 Optimization process of h

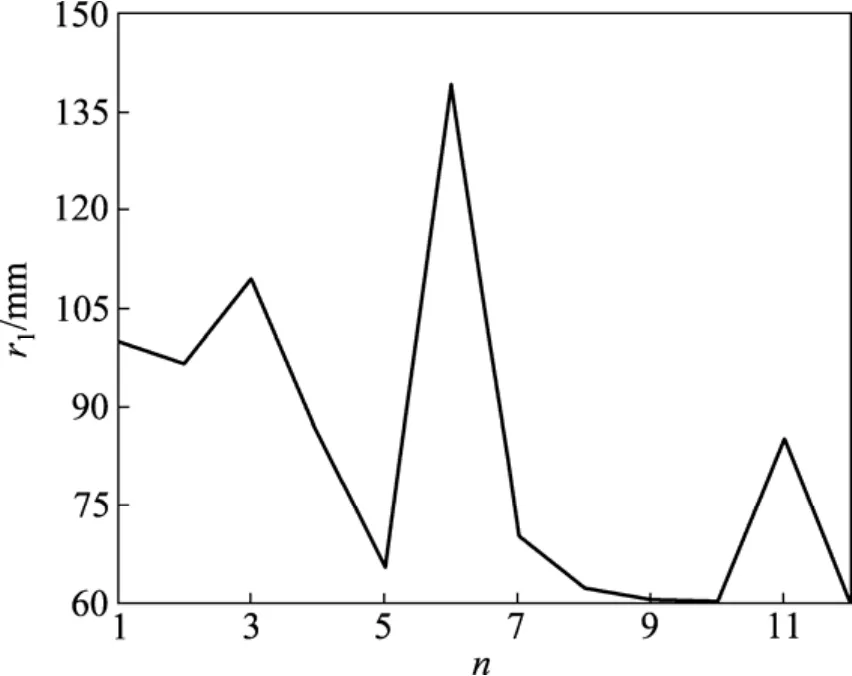
图5 r1优化进程Fig.5 Optimization process of r1

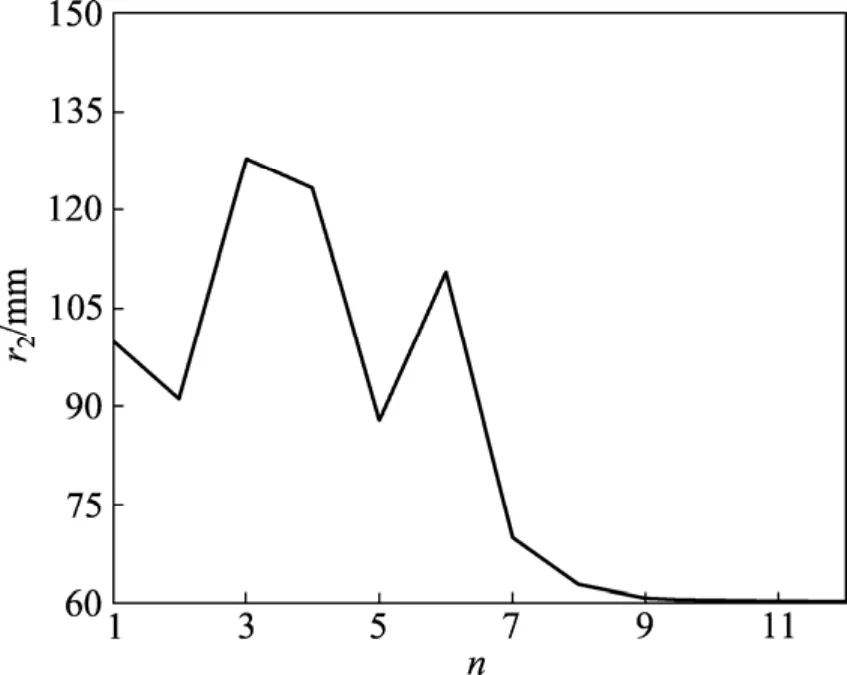
图6 r2优化进程Fig.6 Optimization process of r2

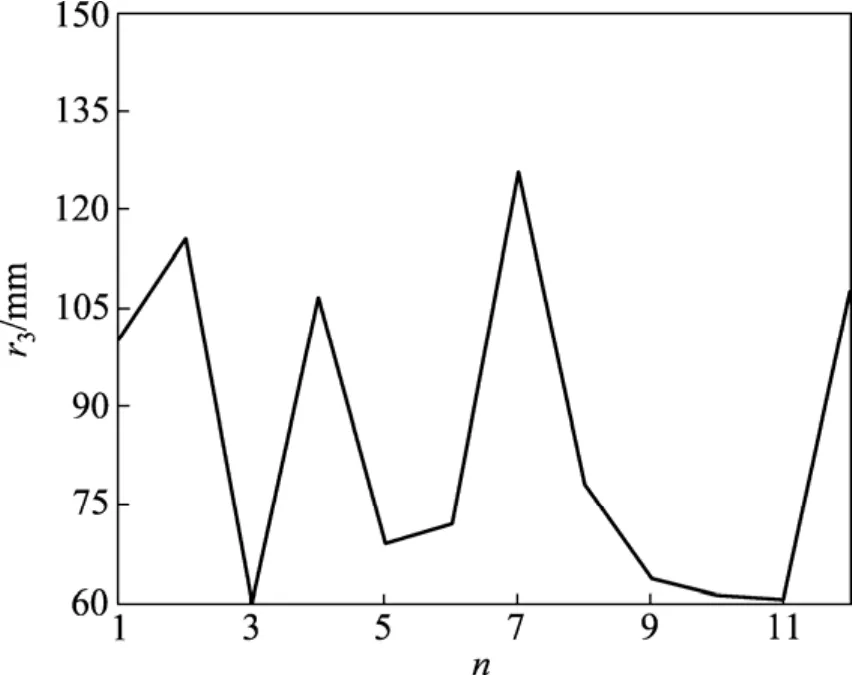
图7 r3优化进程Fig.7 Optimization process of r3

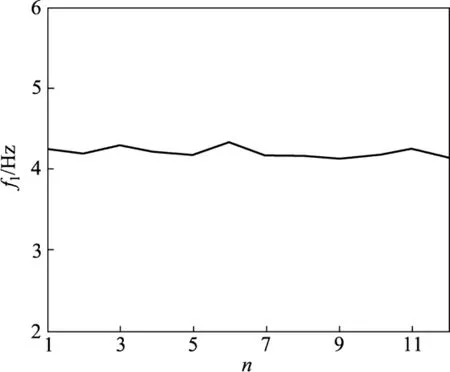
图8 f1优化进程Fig.8 Optimization process of f1

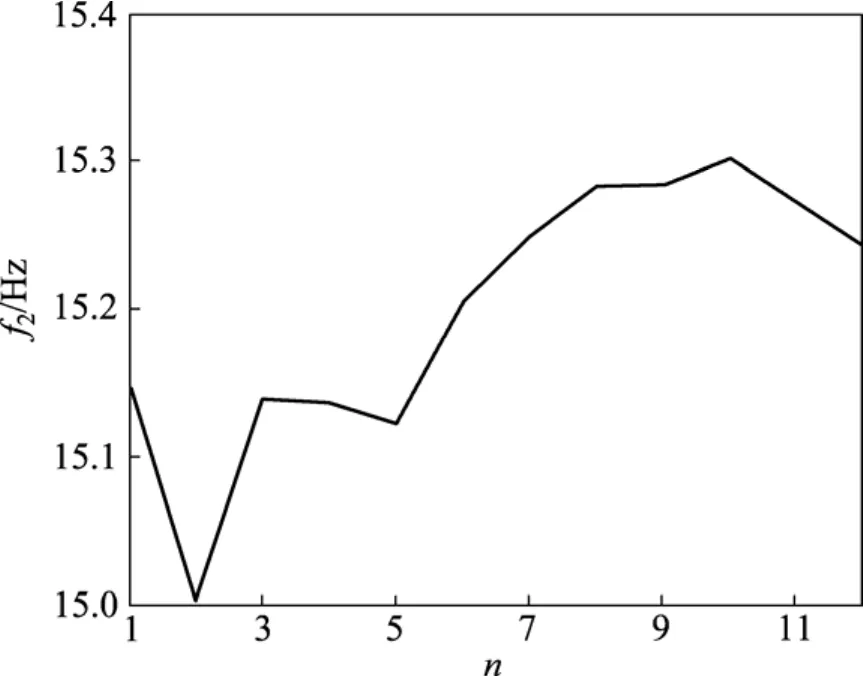
图9 f2优化进程Fig.9 Optimization process of f2

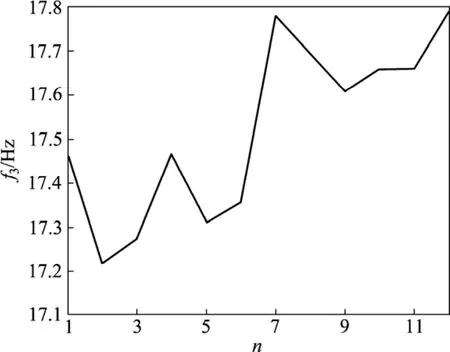
图10 f3优化进程Fig.10 Optimization process of f3

4.2 振动筛优化后的整体效果评估与分析

筋板的尺寸优化后，根据最优结果对整个振动筛结构进行修改，其结构模型及有限元模型如图11和12所示。再次分析其固有特性，计算出整个振动筛的前12阶固有频率和振型，结果如表3所示。

从表3可知：经过结构尺寸优化后，振动筛弯曲变形频率有了较大的提高，第10～12阶模态频率与优化前相比提高了7～18 Hz，说明筛体整体刚度提高。与工作频率比较接近的第7，8和9阶模态频率是对结构影响较大的变形频率，分别由优化前的16.09，18.07和19.83 Hz变为18.37，20.29和24.39 Hz。结构优化后第7阶和第8阶模态振型如图13和14所示，相对应的振型位移Dmx为0.70 mm和0.54 mm。

表2 侧板优化相关参数Table2 Optimization parameters of side plate

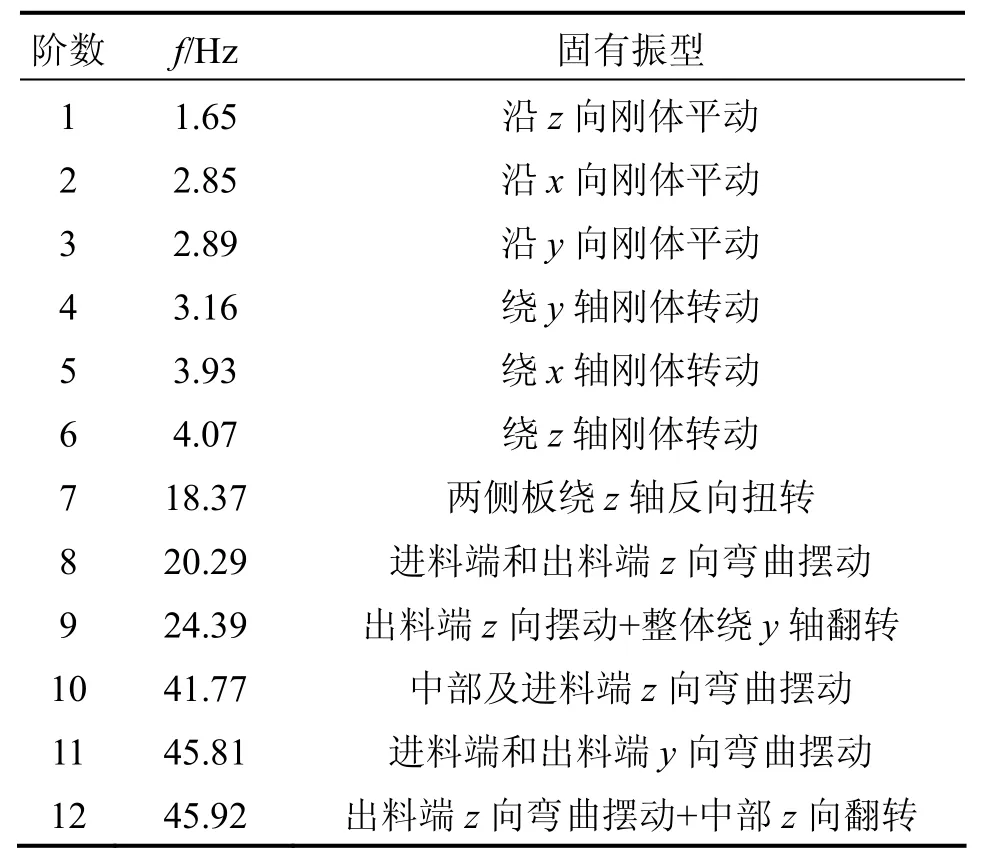
表3 振动筛的模态计算结果Table3 Modal calculation results of vibrating screen

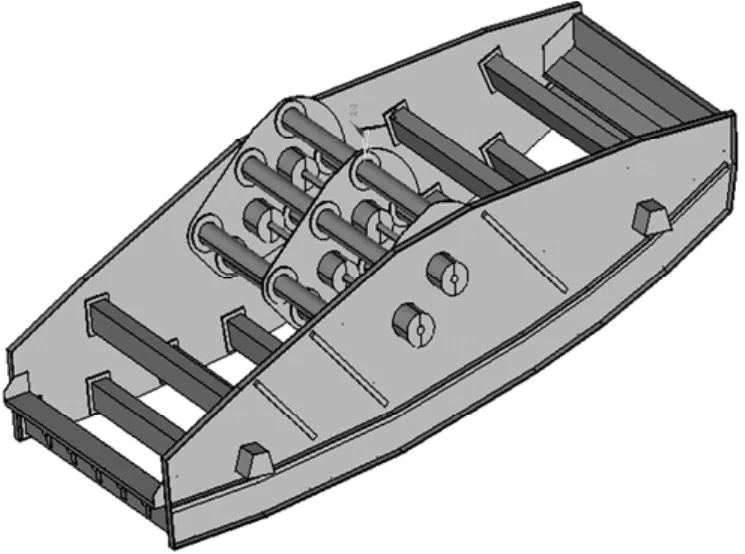
图11 结构模型Fig.11 Structural model

图12 有限元模型Fig.12 Finite element model

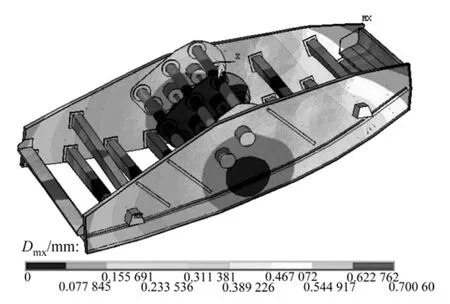
图13 第7阶振型Fig.13 Seventh vibration mode

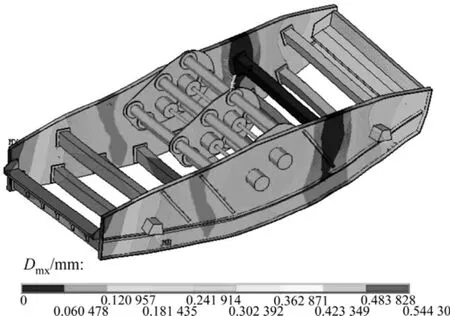
图14 第8阶振型图Fig.14 Eighth vibration mode

将振动筛优化前后相关的参数进行比较，结果如表4所示。由表4可知：优化后振动筛的第1阶弹性变形频率提高 14.17%，第 2阶弹性变形频率提高了12.29%，振动筛总质量减少2.35%。可以说经过筋板尺寸优化后节约了材料，提高了筛板的刚度，降低了筛板的变形，提高了结构的稳定性。

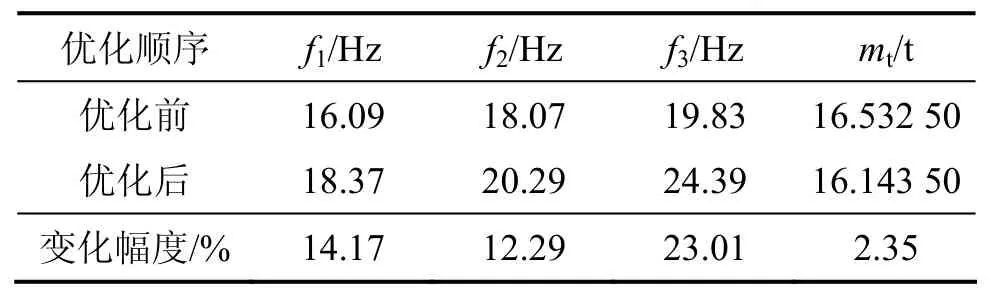
表4 振动筛优化相关参数Table4 Relevant Parameters of Vibrating Screen

5 结论

(1) 在振动筛的加强筋板尺寸优化过程中，将解析灵敏度计算方法嵌入结构优化程序中，考虑变量参数的灵敏度特性，使结构修改灵活有效，提高了程序计算效率，得到了较稳定的优化结果。

(2) 以振动筛侧板质量为目标函数，得到了满足多个频率约束条件的侧板的最小质量。优化后单个侧板质量降低 8.27%，节省了材料，降低了振动筛的工程造价。

(3) 在结构的优化设计中，考虑动力学因素的影响，以多个模态频率作为动态控制参数，给出了适合多频约束的求解准则，简化了递推公式中的参数因子ζj。

(4) 对振动筛加强筋板的尺寸进行优化后，侧板质量降低8.27%，2阶弹性变形频率分别提高了1.37%和 2.97%，达到比较好的优化效果。对优化后振动筛进行评估，其质量降低了 2.35%，与工作频率比较接近的3阶弹性变形模态频率分别提高14.17%，12.29%和23.01%。优化后振动筛的固有频率提高，筛板的刚度增加，模态频率远离激振电机的工作频率，从而提高了结构的稳定性。

[1] 李惠彬. 振动理论与工程应用[M]. 北京: 北京理工大学出版社, 2006:235-248.

LI Hui-bin. Vibration theory and engineering application [M].Beijing: Beijing Institute of Technology Press, 2006: 235-248.

[2] 刘惟信. 机械最优化设计[M]. 第 2版. 北京: 清华大学出版社, 1994: 196-224.

LIU Wei-xin. Mechanical optimization design[M]. 2nd ed.Beijing: Tsinghua University Press, 1994: 196-224.

[3] 焦红光, 赵跃民, 骆振福, 等. 概率筛面的参数优化研究[J].中国矿业大学学报, 2006, 35(3): 384-388.

JIAO Hong-guang, ZHAO Yue-min, LUO Zhen-fu, et al.Parameters optimization of probability screen plane [J]. Journal of China University of Mining & Technology, 2006, 35(3):384-388.

[4] 翟宏新, 杨丽, 李君. 工业型弛张筛系统参数的整体优化[J].煤炭学报, 2004, 29(1): 105-108.

ZHAI Hong-xin, YANG Li, LI Jun. Integral optimization on systematic parameters of flip-flow screens [J]. Journal of China Coal Society, 2004, 29(1): 105-108.

[5] Volker W, Matthias S, Heimo G. Working with characteristic curves for the optimization of sizing on circular vibrating screens[J]. Mineral Processing, 2007, 48(7): 14-29.

[6] Taroco E, Feijoo R A. A unified approach for shape sensitivity analysis of elastic shells [J]. Structural and Multidisciplinary Optimization, 2004, 27(1/2): 66-79.

[7] Park C K, Kim W J, Lee S, et al. Positive sensitivity analysis in linear programming [J]. Asia-Pacific Journal of Operational Research, 2004, 21(1): 53-68.

[8] 梁醒培, 陈长冰. 频率约束优化设计方法及工程应用[J]. 机械设计, 2006, 23(5): 36-38.

LIANG Xing-pei, CHEN Chang-bin. Designing method and engineering application on optimization of frequency constraint[J]. Journal of Machine Design, 2006, 23(5): 36-38.

[9] 张成勇. 一种超静定网梁激振大型振动筛: 中国,02112809.X[P]. 2003-10-08.

ZHANG Cheng-yong. A type of large vibrating screen with hyperstatic net-beam vibrating screen: China, 02112809.X[P].2003-10-08.

[10] 马富强. 振动筛动态特性浅析[J]. 矿山机械, 1996, 24(6): 40.

MA Fu-qiang. Dynamic characteristics analysis of vibrating screen[J]. Mining & Processing Equipment, 1996, 24(6): 40.

[11] 陈劲, 张泽鹏. 频率约束下的桥梁结构优化设计探讨[J]. 中南公路工程, 2001, 26(4): 67-69.

CHEN Jin, ZHANG Ze-peng. Optimization design research on bridge construction under frequencies constraints [J]. Central South Highway Engineering, 2001, 26(4): 67-69.

[12] 王荣昌, 应稼年, 王文亮. 结构优化设计中的灵敏度分析[J].振动与冲击, 1996, 15(1): 1-4.

WANG Rong-chang, YING Jia-nian, WANG Wen-liang.Sensitivity analysis for structural optimal design[J]. Journal of Vibration and Shock, 1996, 15(1): 1-4.

[13] Grandh R. Structural optimization with frequency constrains: A review[J]. AIAA Journal, 1993, 31(12):2296-2304.

[14] Powell M J D, Grippo L. A method for nonlinear constraints in minimization problems[C]// Fletcher R. Optimization. New York:Academic Press, 1969: 283-298.

[15] Khot N S. Optimization of structures with multiple frequency constraints [J]. Computers and Structures, 1985, 20(5): 869-876.