一种实时轮廓误差估算方法

李培新 马 跃 于 东 王志成, 韩 旭

1.中国科学院研究生院,北京,100049 2.中国科学院沈阳计算技术研究所高档数控国家工程研究中心,沈阳,110171 3.沈阳高精数控技术有限公司,沈阳,110171

0 引言

轮廓误差的计算是高档数控系统的一个重要研究课题。目前离线计算轮廓误差的方法很多[1-4],虽然这些方法的计算精度很高,但是由于其计算复杂、计算时间较长,很难应用到实时计算轮廓误差的任务中。实时计算轮廓误差方法在工程上可以指导控制参数的选取,并为实时轮廓误差控制方法(如交叉耦合控制方法)提供支持[5-7]。目前,许多研究实时估算轮廓误差的方法中,轮廓误差的估算与跟随误差直接相关[8-11]。然而,这些轮廓误差估算方法对跟随误差的依赖性很大,估算的精度有待进一步提高,如Yeh等[8]提出的实时轮廓误差估算方法,对跟随误差有比较苛刻的要求。从数学上分析,计算轮廓误差最直接和有效的方法是计算反馈点到指令曲线的最短距离。这种方法计算的轮廓误差计算精度高,然而对于任意加工曲线,这种方法计算时间长,计算复杂,适合离线计算。为了达到实时估算轮廓误差的要求,需要将其作相应的简化。本文对上述离线计算方法进行修改,提出一种轮廓误差实时估算方法,该方法具有计算量小和精度高的优点,能够满足多种工程需要。

1 离线轮廓误差计算

1.1 线性轨迹命令下的轮廓误差

图1给出了线性轨迹命令下的轮廓误差计算方法,图中,P为实际位置点,R为指令位置点,ε为轮廓误差,e为跟随误差。

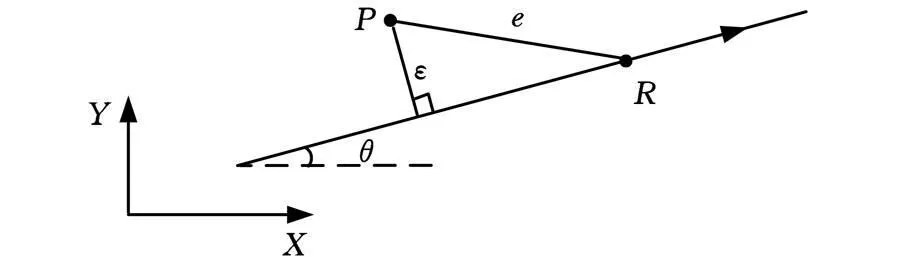
图1 线性轨迹命令下轮廓误差计算

由图1可知,ε为点P到指令轨迹(直线)的距离。设点P的坐标为(x′,y′),指令轨迹方程为

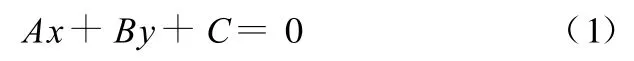
则

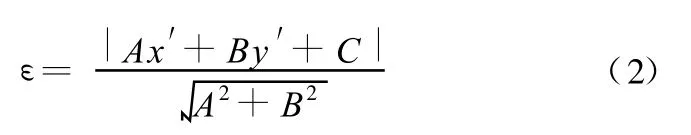
1.2 曲线轨迹命令下的轮廓误差

图2给出了曲线轨迹命令下的轮廓误差计算方法。由图2可知,ε为点P到指令轨迹(曲线)的最近距离。如果知道了指令的轨迹方程,则点P到曲线的距离便可以计算出。求点到曲线的距离,工程上有许多方法,如最优化理论。此方法要求首先求出指令曲线的方程,然后根据最优化理论将点P到曲线的最短距离求出,即得到点P到指令轨迹的轮廓误差。

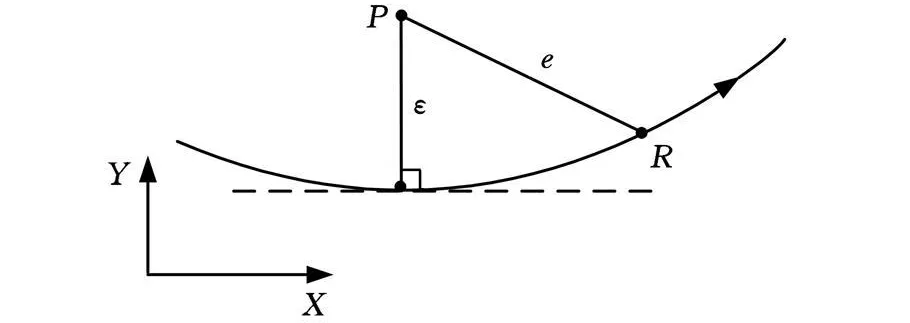
图2 曲线轨迹命令下的轮廓误差计算

在重构数控系统加工轮廓曲线的方法中,分段样条插值法能很好地反映原曲线的形状,所以可以将分段差值得到的曲线作为原轮廓曲线。本文分别采用分段线性样条插值和三次样条插值离线重构的方法加工轮廓曲线。实际上,线性插值可以反映原曲线的整体特性,经过三次样条插值后,曲线变得连续、平滑,然后分别求出线性插值后的轮廓误差曲线和三次样条插值后的轮廓误差曲线作为轮廓误差曲线的基准。求解的过程采用最优化原理,将问题转化为非线性约束规划问题来求解。

1.2.1 线性插值轮廓误差计算

线性样条插值是最简单的样条插值。数据点使用直线进行连接,结果样条是一个多边形。从代数的角度来看,每个分段函数si都是一个如下的线性函数：

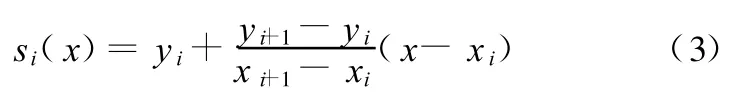
样条的每个数据点都必须连续,即

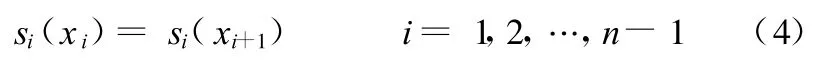
这样,轮廓误差的计算可如图3所示。

图3 线性插值轮廓误差计算

图3中,P为实际反馈点位置,轮廓误差ε即为点P到指令点Ri与Ri+1之间轨迹的最短距离。令点Ri+1的坐标为(xi+1,yi+1),点Ri的坐标为(xi,yi),则点Ri、Ri+1之间的轨迹方程如式(3)所示。其中Ri为离点P最近的指令点,轮廓误差ε的计算表达式如式(2)所示。

1.2.2 三次样条插值轮廓误差计算

对于给定的数据点(xi,yi),y i=f(xi),i=0,1,…,n。用n段三次多项式在数据点之间构建一个三次样条。如果

表示对函数f进行插值的样条函数,则仍需要以下条件：

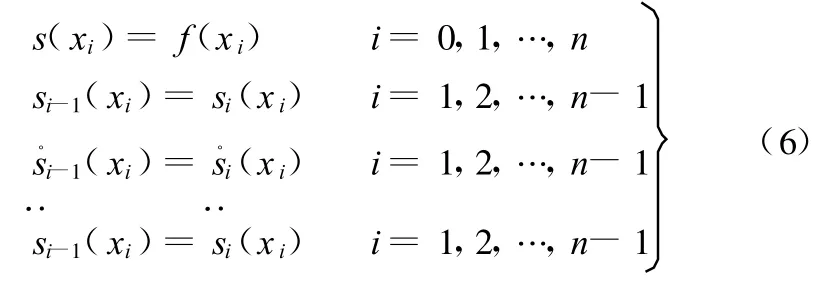
设s¨(x0)=s¨(xn)=0,这样总共有4n个已知条件,从而可确定n段多项式,轮廓误差的计算可由图4得出。点Ri与Ri+1之间的曲线轨迹方程为

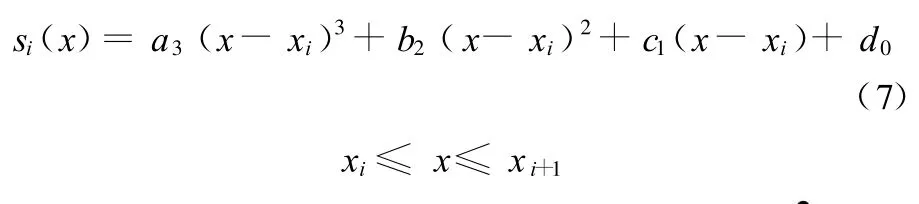
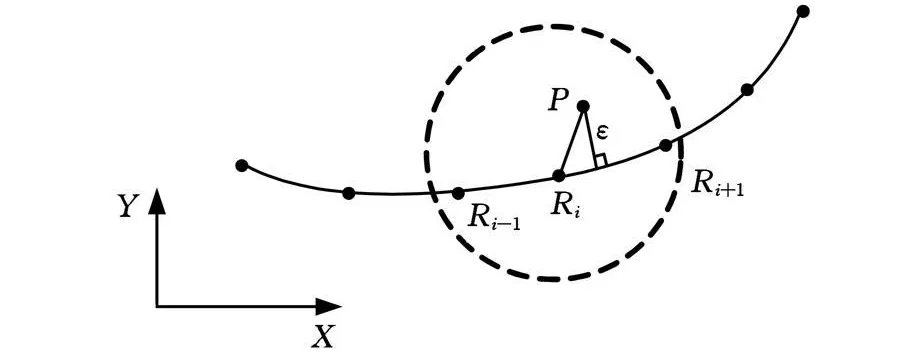
图4 三次样条插值轮廓误差计算

轮廓误差ε即是点P到si(x)的最短距离,将求解过程转化为非线性约束规划问题如下：

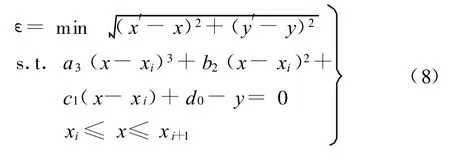
2 实时轮廓误差估算

由上文分析可知,对于轮廓误差的计算,特别是三次样条插值轮廓误差的计算,计算复杂且计算量大,很难应用到实时系统中。为此,本文提出了一种修正的轮廓误差估算方法,并给出了该算法的实时性分析。

2.1 实时轮廓误差估算算法

图5给出了实时轮廓误差的估算方法。图5中,点Ri为离点P最近的指令位置点,Ri-1、Ri+1分别是点Ri的直接前驱点和直接后继点。实际上,由于直接计算ε计算量大,不能实现实时计算的要求,所以需要一种简便且估算准确的方法来代替ε的计算。本文用ˆε来代替ε作为轮廓误差的估计。ˆε的计算方法如下：

图5 实时轮廓误差估算

将Ri-1、Ri+1的连线作为曲线在点Ri处的切线向量τ。设点 Ri-1的坐标为(xi-1,yi-1),点Ri+1的坐标为(xi+1,y i+1),点 Ri的坐标为(xi,y i),则过点Ri-1、Ri+1的直线的斜率k为

用k来代替指令曲线在点R i处的切向量τ,那么过点Ri的切线方程为

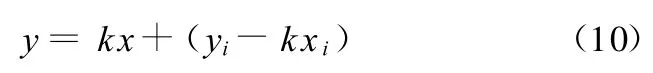
化为直线的一般方程为

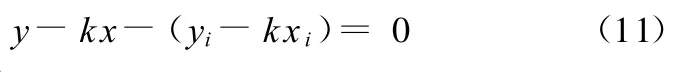
则点 P(x′,y′)到直线(式(10))的距离ˆε为

将ˆε作为ε的代替。注意：用此方法计算斜率k时,当k为无穷大时,即 xi+1-xi-1=0时,

在该算法中,寻找离点P最近的指令位置点Ri的具体方法是：以当前的指令位置点Rj向前找,计算|PRi|2(1≤i≤j),即点P、Ri之间距离的平方,避免开根号的运算量,当发现当前|PRi-1|2比|PRi|2大时停止搜索,点Ri即是离点P最近的指令点。实际上,由于点P与其跟随点R距离不会很远(轮廓误差控制的方法也在减小跟随误差,使点P逼近点R),所以只需要向前搜索很小一个常数点的位置即可以找到Ri,在下文的实验中平均只需前找十几个点位置即可以找到Ri。

由上述方法分析可知,当指令轨迹为线性时,ˆε即是ε。因为 ,过点Ri-1、Ri+1的直线的斜率k即为线性轨迹的斜率,过点Ri线率为k的方程即是式(1),ˆε的计算可采用式(2)。当指令轨迹为不规则曲线时,ˆε或大于、或小于ε。在下文的实验中将给出ˆε与ε之间误差的对比分析。

实际上,在轮廓曲线重构的方法中样条插值法具有很高的精度,本文提出的轮廓误差实时估算方法,将曲线在各点的切线用前后两点的连线代替,见式(9),即如果共有n+1个指令点,按这种方法参考式(5)与式(6)可得出4n个已知条件(已有条件2n+2个、内部条件2n-2 个,令这样就可重构出轨迹指令的轮廓曲线,并且重构的曲线也能很好地反映曲线的原形状。而本文提出的方法正是以此重构轮廓曲线方法为理论基础加以修改得出轮廓误差的估算,这样从理论上可以保证其算法的正确性。

2.2 算法实时性分析

由上述的阐述可以发现,此方法所需的主要运算时间有求根运算1次、绝对值运算1次、除法运算1次,完全可以满足实时运算的要求,在下文的实验中给出了其运算时间。相对于插值法的算法时间复杂度O(n2)和大量的运算(式(5)、式(6)、式(8)),本文提出的实时估算方法计算简单,运算量小。

3 实验

两个轴的实时轮廓误差估算实验装置采用的伺服和电机均由沈阳高精数控技术有限公司提供,伺服型号为 GJS-015ADA,电机型号为GJM096ADB22。CNC和伺服电机通过运动控制总线相连,CNC的插补命令通过运动控制总线发给指定的伺服,伺服的反馈响应也通过运动控制总线传给CNC。为了实时地估算轮廓误差,需要实时地从总线上获取当前位置信息(包括指令位置和实际反馈位置),然后依据上文给出的方法估算轮廓误差。由于实验只涉及到两个轴,所以实验中只是向X轴和Y轴发送插补数据,并采集相应的反馈数据,没有用到其他轴,如Z轴。

3.1 实时分析实验

线性样条插值轮廓误差的计算和三次样条插值轮廓误差的计算不考虑样条插值的时间,即假设轮廓曲线已经给出,仅计算轮廓误差运算的时间,表1给出了其运算时间对比。

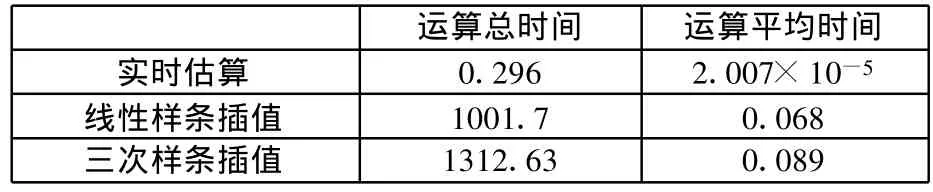
表1 运算时间对比 s

实验中,插补器每隔0.25ms发送一个插补位置点,总共发送n个插补点。因而平均每个反馈点轮廓误差计算所需的时间等于总时间除以插补点数。如表1所示,在这0.25ms的周期内实时估算的方法完全可以完成轮廓误差的计算,每个点的平均计算时间只需要0.02ms,由此可以证明提出的实时估算轮廓误差方法满足实时计算的要求。

3.2 实时估算精度实验

在采样点密集的情况下,线性插值可以反映轮廓曲线的整体特性,三次样条插值可以连续平滑地重构出轮廓曲线。本实验中每隔0.25ms采一个样点,由于采样点较密集所以本文将εrt(实时估算轮廓误差)分别和εliner(线性插值重构轮廓误差)与εspline(三次样条插值重构轮廓误差)作比较,以求给出准确的对比。图6所示为双轴实验加工的轮廓曲线,图7给出了实时估算的轮廓误差曲线图,图8所示为实时估算的轮廓误差εrt分别与基准轮廓误差εliner和εspline作差比较的误差曲线。

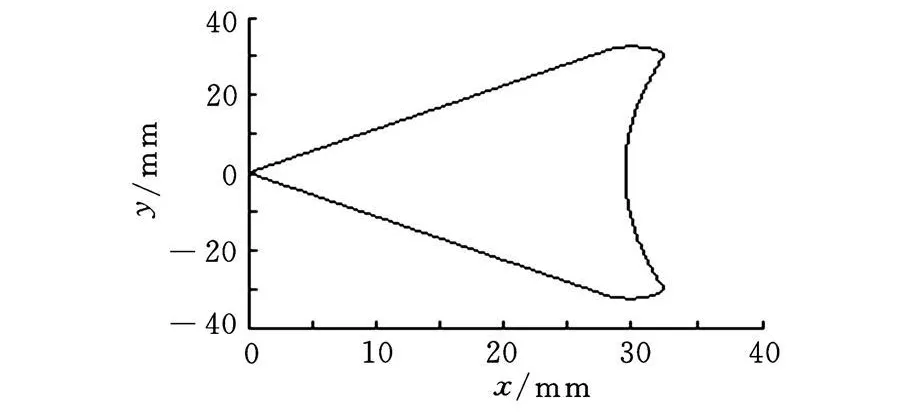
图6 实验加工曲线

图7 实时轮廓误差曲线

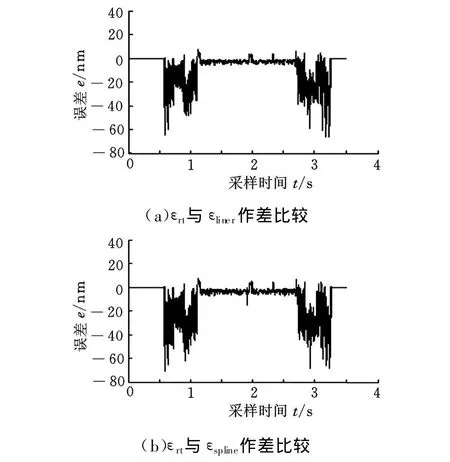
图 8 εrt与 εliner、εspline作差比较

为了较明显地给出对照 ,将 εrt与 εliner、εspline在数学分析上作比较,如表2所示。

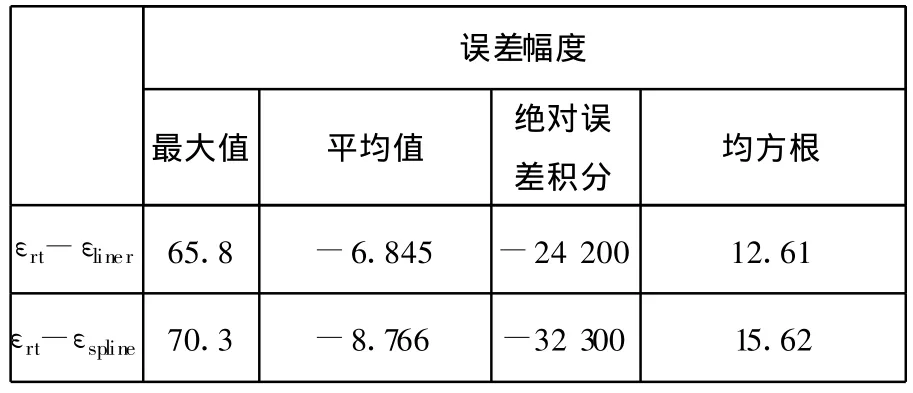
表 2 εrt与 εliner、εspline的差值 nm

由表2可以发现,实时估算的轮廓误差εrt和基准轮廓误差εliner、εspline之间的平均差值为纳米级别,说明该估算方法在提高实时性的同时,牺牲的精度很小,完全可以满足实际工程的应用需要。

4 结语

本文分析了离线计算轮廓误差的方法,在此基础上提出了实时估算轮廓误差的新方法,通过实验证明该方法实时性好,估算精度高。该方法简单明了,可以应用到数控系统上实时估算轮廓误差。在工程上可以指导控制参数的选取,并为实时轮廓误差控制方法,如交叉耦合控制方法,提供误差控制支持。

[1] 郭慧,林大钧.基于微粒群算法的复杂曲面轮廓度误差计算[J].东华大学学报(自然科学版),2008,34(3)：274-277.

[2] 侯宇,张竞,崔晨阳.复杂线轮廓度误差坐标测量的数据处理方法[J].计量学报,2002,23(1)：13-16.

[3] 廖平.基于粒子群算法和分割逼近法的复杂曲面轮廓度误差计算[J].中国机械工程,2010,21(2)：201-205.

[4] Yu Yuan,Lu Jun,Wang Xiaochun.Modeling and Analysis of the Best Match in Free-form Surface Measuring[J].Mechanical Science and Technology,2001,20(3)：19-20.

[5] Koren Y.Cross-coupled Biaxial Computer for Manufacturing Systems[J].Trans.ASME,J.Dyn.Syst.Meas.Control,1980,102(4)：265-272.

[6] Koren Y,Lo C C.Variable Gain Cross Coupling Controller for Contouring[J].CIRP Proc.Manufacturing Systems,1991,40：371-374.

[7] Ramesh R,Mannan M A,Poo A N.Tracking and Contour Error Control in CNC Servo Systems[J].Int.J.Mach.Tools Manuf.,2005,45：301-326.

[8] Yeh S S,Hsu P L.Estimation of the Contouring Error Vector for the Cross-coupled Control Design[J].IEEE/ASME Trans.on Mechatronics,2002,7(1)：44-51.

[9] Cheng M Y,Lee C C.Motion Controller Design for Contour-following Tasks Based on Real-time Contour Error Estimation[J].IEEE Transactions on Industrial Electronics,2007,54(3)：1686-1695.

[10] Chen S L,Wu K C.Contouring Control of Smooth Paths for Multiaxis Motion Systems Based on E-quivalent Errors[J].IEEE Trans.Control Syst.Technol.,2007,15(16)：1151-1158.

[11] 周凯.数控原理、系统及应用[M].1版.北京：机械工业出版社,2007.