滚动导轨结合面动态特性参数识别实验研究
张 华 袁军堂 汪振华
南京理工大学,南京,210094
0 引言
对于数控机床而言,滚动导轨是广泛应用的功能部件。由于滚动结合面为线接触或点接触,刚度相对较弱,往往是数控机床整体结构的薄弱环节,从而影响数控机床的加工精度。为了准确获取滚动导轨结合面动态特性参数,国内外学者进行了相关探索与研究[1-5]。本文建立了识别滚动导轨结合面动态特性参数的测量模型,该测量模型将安装有滚动导轨的机构简化为单自由度系统并消除了基础位移对参数识别的影响。基于测量模型研制了滚动导轨结合面动态特性参数测量装置,并针对施耐博格MRC45型导轨进行了实验,获得了其法向和侧向动态刚度及阻尼数据。
1 滚动导轨结合面动态特性建模
一般情况下,滚动导轨安装在基座(如机床床身)上,而运动部件(如工作台)连接在滑块上。滑块和导轨之间通过滚动体(如滚珠、滚柱)连接,它们之间为点接触或线接触,而导轨与基座以及运动部件与滑块之间都为螺栓连接,刚度远大于导轨—滚动体—滑块之间滚动接触面的接触刚度。因此,通过合理设计,增大基础和运动部件的刚度,在一定的振动频率范围内可以将基础部件和运动部件视为刚性体。这样就可将运动部件及滑块看成质量块,滚动结合面看作弹性及阻尼元件,从而可得到如图1所示振动系统。
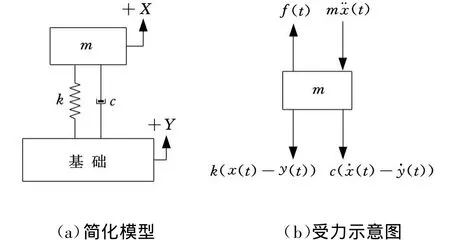
图1 力学模型
对于图1a所示系统,当质量块m受到外界简谐激振力f(t)作用时,系统受力情况如图1b所示,其振动方程可以表示为
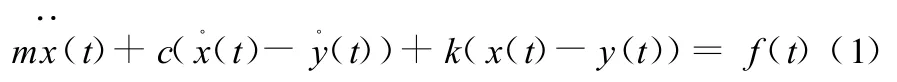
式中,m为运动部件与滑块的总质量;k、c分别为滚动导轨结合面的刚度和阻尼;x(t)、y(t)分别为质量块和基础的位移。
对式(1)作以下变换构成单自由度振动方程:
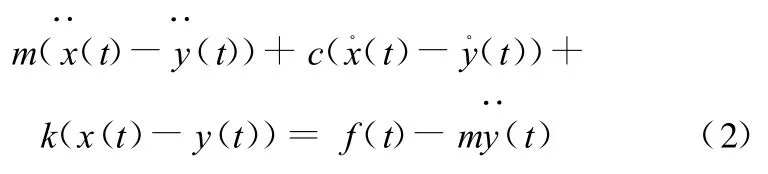
在简谐激振力作用下,f(t)、x(t)及y(t)可用复向量表示 :f(t)=F ejωt,x(t)=X ejωt,y(t)=Y ejωt(F 、X 、Y 分别表示f(t)、x(t)和 y(t)的有效值和初始相位)。将以上三项代入式(2)可得
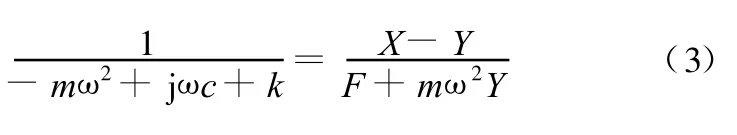
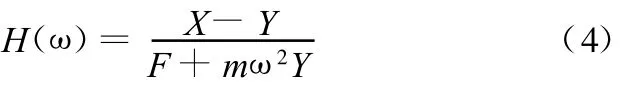
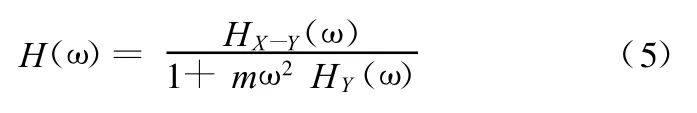
式中,HX-Y(ω)为运动部件频响函数与基础频响函数差;HY(ω)为基础频响函数。
HX-Y(ω)和 HY(ω)可由实测数据计算得到。由以上推导可知,H(ω)是一个等效单自由度系统的频响函数,等效单自由度系统的质量m为运动部件与滑块的总质量,刚度和阻尼分别为滚动导轨结合面刚度和阻尼。由频响函数曲线可识别出系统固有频率ωn,然后可根据下式求出滚动导轨结合面的动态刚度及阻尼:

阻尼比ξ可根据H(ω)幅值曲线采用半功率带宽法求取。如图1b所示,基础位移影响弹簧和阻尼器的受力状况,本文从力学模型中消除基础位移的影响更符合实际,识别出的参数精度高且具有理论依据。
2 测试系统设计
根据测量模型设计了滚动导轨结合面动态特性参数测试装置,图2所示为法向激振时测试装置结构图,测试装置采用双导轨结构,通过桥板连接两滑块,激振器在桥板上表面中心位置对装置进行激振。侧向激励点如图2中的9所示 ——为便于侧向加载,在桥板另一侧对称加工了阻抗头连接螺纹孔,用于侧向激振。
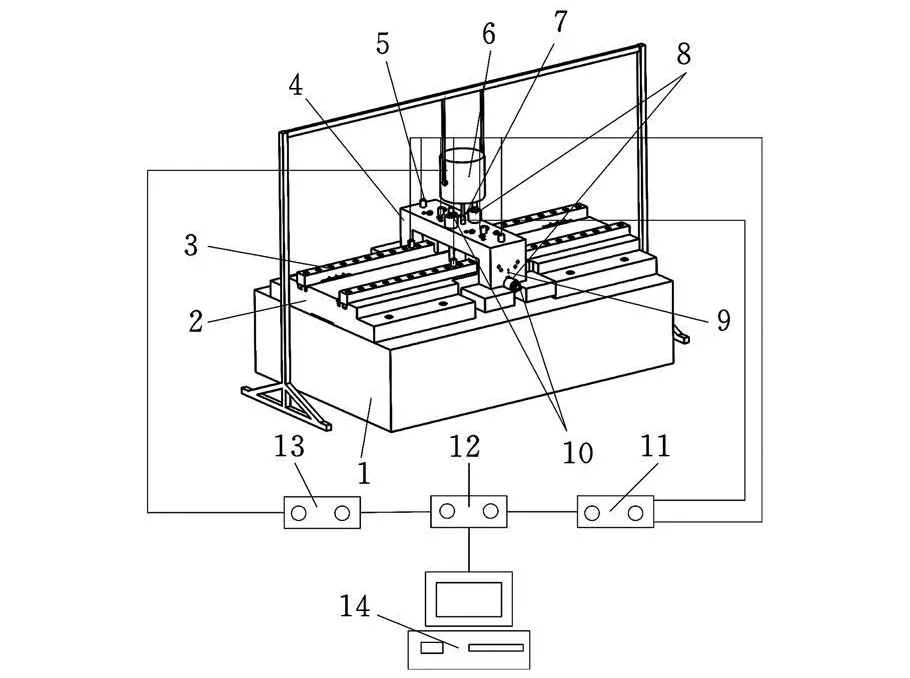
图2 测试装置结构图
如图2所示,测试时首先在模态分析软件14中设置各参数,数字采集器12发出的扫频信号经功率放大器13放大后传送至激振器6,激振器连接阻抗头7并对实验台激励。力信号由阻抗头拾取,加速度信号由加速度传感器5测得,两者经电荷放大器11后转变为适量大小的电压信号,并由数据采集器采集。计算机最终得到的是经数据采集器模数转换的力和加速度值,通过模态分析系统傅里叶变换后即可获得各测点频响函数。测试仪器的型号和主要参数见表1。
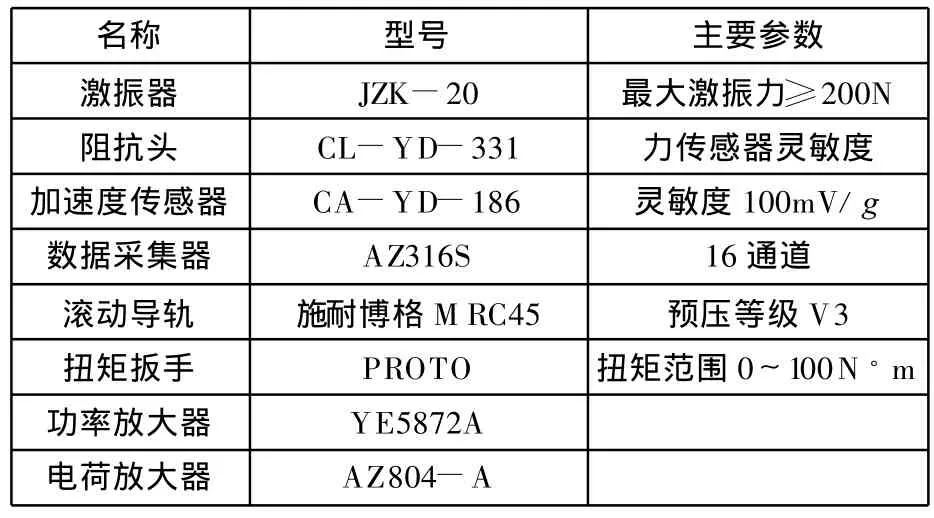
表1 模态试验仪器
3 测试结果与分析
3.1 系统测试
为验证测试系统的准确性,对实验导轨在未加载状态下(载荷仅为桥板重量)侧向动态刚度及阻尼进行测量与识别,通过对系统振型、测点频响函数及H(ω)曲线的检验来判别测试结果的准确性。
系统振型从以下两方面检验:一是测量模型中将桥板及滑块视作整体,因此桥板与滑块应保证同步平动;二是对于两自由度无阻尼系统,在简谐激振力作用下,两质点以相同的频率和相角但不同的振幅做简谐振动。图1a简化模型中,阻尼值c较小,系统为弱阻尼系统,因此在系统固有频率下桥板与滑块应和基础近似做相对平动。本文所使用的安正CRAS模态分析软件振型动画功能可显示各测点相对运动关系,因此在桥板、滑块及基础上合理布置测点,测试结束后就可观察它们之间的相对运动关系,经检验测试装置在450Hz附近振型满足以上要求。
频响函数HX-Y(ω)、HY(ω)以及 H(ω)都由测点实验数据计算得到,因此测点实验数据准确可靠对识别结合面动态特性参数至关重要。根据测量模型,桥板和基础测点频响函数曲线都应为单自由度曲线;本文振动信号由加速度传感器测得,因此桥板和基础测点频响函数幅值A1及 A2都为加速度和力的比值。
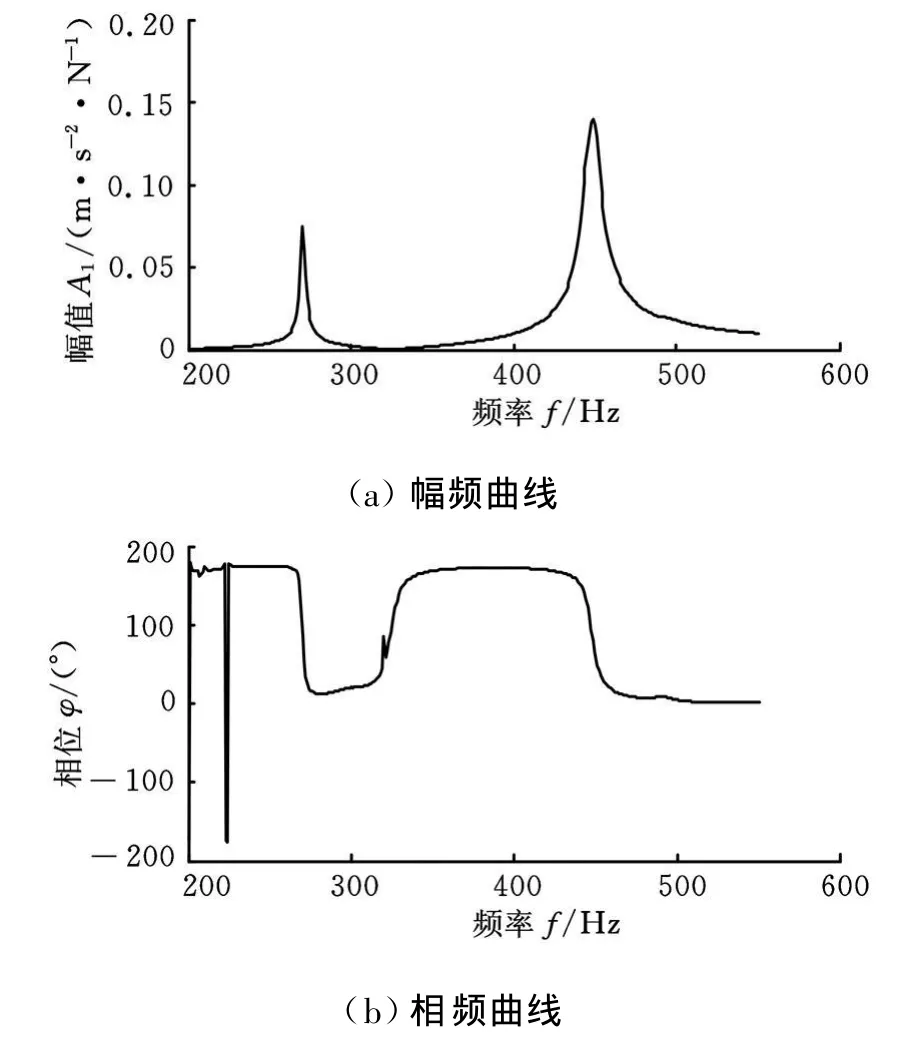
图3 桥板测点频响函数曲线
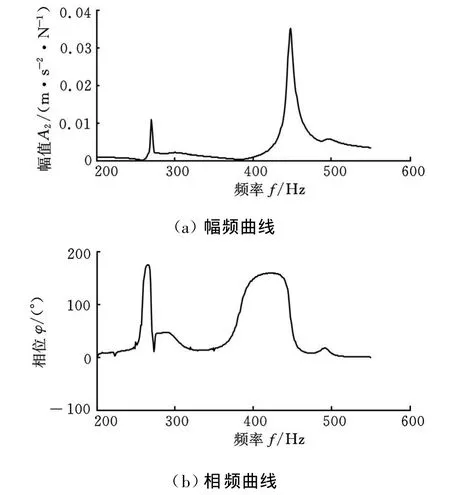
图4 基础测点频响函数曲线
图3、图4所示分别为桥板与基础上某测点频响函数曲线。从图中可以看出:在270Hz及450Hz附近频段内两者都为较好的单自由度曲线,但270Hz频率点处桥板振型为两侧摆动型,为桥板自身模态,不符合上文所述振型要求。图5为根据式(5)计算得到的H(ω)幅频和相频曲线 ——求取H(ω)时对测得的加速度进行了二次积分,因此 H(ω)幅值A3为位移和力的比值。从图5可以看出,幅频曲线在450Hz附近达到峰值,相位在峰值频率附近发生了180°转变,为典型的单自由度振动曲线。
将系统固有频率ωn代入式(6)可以得到未加载状态下该滚动导轨结合面侧向动态刚度kc=3.6×108N/m。阻尼比ξ可由半功率带宽法求取,根据 H(ω)幅频曲线计算得到该滚动导轨未加载时侧向阻尼比ξc=0.64%,侧向阻尼值cc=1678 N◦s/m。法向刚度和阻尼的测量与侧向类似:未加载状态下导轨结合面法向动态刚度 kf=3.7×108N/m,法向阻尼比ξf=0.54%,法向阻尼值c f=1388N◦s/m。
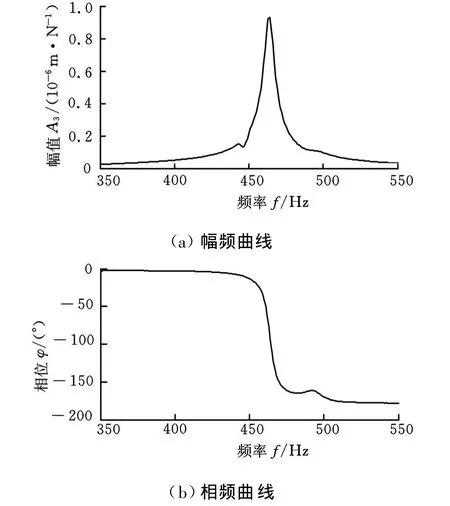
图5 等效单自由度系统频响函数曲线
3.2 载荷对滚动导轨结合面动态特性参数的影响
对于机床而言,安装在导轨上的运动部件重量各异,而且加工工件重量及切削力也会发生变化,因此滚动导轨所受载荷会随着不同的加工状态发生变化,分析不同载荷下滚动导轨结合面动态特性参数的变化规律对指导机床设计具有重要意义。如图2所示:M12双头螺栓10连接安装平台2和桥板4对导轨法向及侧向进行组合加载,为了减小螺栓对刚度测量的影响,在施力螺栓上加上较厚的橡胶圈8;测量时通过扭矩扳手调节施力螺栓预紧力对滚动导轨结合面进行加载,预紧力F≈T/(0.2d),d为施力螺栓公称直径,T为扭矩。图6所示为实验导轨结合面动态刚度随载荷变化曲线图。由图6可知:①导轨结合面侧向动态刚度随载荷增大而缓慢增大,当载荷达到一定值后刚度趋于稳定,刚度最大变化量在10%左右;②法向动态刚度受载荷影响不明显,刚度在3.75×108N/m左右变化。
4 结论
(1)建立了识别滚动导轨结合面动态特性参数的测量模型,该测量模型将安装有滚动导轨的机构简化为单自由度系统并消除了基础位移对参数识别的影响。根据测量模型研制了滚动导轨结合面动态特性参数识别实验装置,获得了滚动导轨法向及侧向动态刚度精确测量方法。
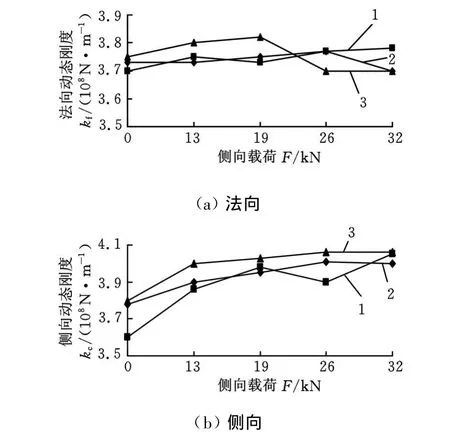
图6 载荷-刚度变化曲线
(2)实验导轨结合面侧向动态刚度随载荷增大而缓慢增大,当载荷达到一定值后刚度趋于稳定,刚度最大变化量在10%左右;法向动态刚度受载荷影响不明显,刚度值保持在3.75×108N/m左右。
[1] 王延忠,周元予,刘强,等.直线电机驱动的加工中心导轨副动力学特性分析[J].中国机械工程,2008,19(13):1574-1576.
[2] 张建润,卢熹,孙庆鸿,等.五坐标数控龙门加工中心动态优化设计[J].中国机械工程,2005,16(21):1949-1953.
[3] Liu Yang,Li Jingkui.Influence of Linear Guide Joint on Dynamic Behavior of NC Machine Tools[J].Journal of Northeastern University(Natural Science),2006,27(12):1369-1372.
[4] 张广鹏,史文浩,黄玉美.机床导轨结合部的动态特性解析方法及其应用[J].机械工程学报,2002,38(10):114-117.
[5] 李磊,张胜文,于洋,等.滚动导轨结合面参数识别及仿真分析[J].江苏科技大学学报,2009,23(2):142-145.

