测试不确定条件下基于贝叶斯网络的装备测试优化选择技术
陈希祥 邱 静 刘冠军
国防科学技术大学,长沙,410073
0 引言
在装备全生命周期的测试性设计过程中,基于测试性分析的测试优化选择是测试性方案优化工作的开始,关系到整个测试性设计工作的好坏[1-2]。目前关于测试性分析与测试选择的研究比较广泛和深入[2-6],并取得了一定的成果,也涌现出了一些辅助分析与设计工具,如DSI公司的eXpress[7]和QSI公司的 TEAMS[8]。但是其理论与方法仍然停留在早期的研究基础之上,即基于确定性测试假设条件,忽略十几种存在的真实情况对模型进行简化。鉴于此,Raghavan等[9]、Sui等[10]考虑了测试不确定性,进行了诊断策略设计或故障诊断的研究。其中,在测试性模型中,故障与测试逻辑关系也表现出不确定性,导致测试性指标的计算以及故障-测试相关性矩阵都将发生改变。如果忽略这种不确定性,而采用传统的诊断推理机,则可能产生不合乎实际情况的测试性分析结果,无法有效指导测试性评估与设计,进而影响测试选择的结论。
为了从根本上避免脱离实际,针对装备系统测试过程中普遍存在的测试不确定性问题,基于传统的多信号流图模型,首先建立面向测试性分析的贝叶斯网络模型,在此基础上通过贝叶斯参数学习算法获得不确定条件下的故障-测试相关矩阵,并提出基于贝叶斯推理的测试性指标形式化描述与计算方法,进而利用混合二进制粒子群-遗传算法(hybrid binary particle swarm optimization and genetic algorithm,HBPSOGA)[6]对系统进行测试优化选择。最后通过案例对所提出的模型和方法进行有效性验证。
1 基于不确定测试的测试性分析模型
1.1 问题描述
装备系统测试性模型的建立有多种方式,其中运用最广泛、效果最明显的是Deb等[11]提出的多信号流模型,通过该模型可以获得基于布尔逻辑的系统故障-测试相关矩阵,进而可对系统进行测试性分析与评估,对于初始阶段的测试性设计而言能够满足需要。但上述模型并没有考虑测试过程中的不确定性,其约束条件在实际测试性设计中往往是不完备的,导致该模型缺乏对不确定信息的处理能力,对装备测试性分析的结果过于乐观。由于装备复杂的内部结构和外界环境,实际中的测试结果会受到许多干扰源的影响,包括不正确的安装、错误的人为操作、电磁干扰、环境影响以及测试设备固有的测量误差等,这些难以用传统模型描述的运行状态和工况都会影响测试结果的可信度,因而有必要构造具有处理不确定性信息能力的测试性分析模型。
本文立足于测试实际情况,考虑不确定因素,对多信号流图模型进行扩展,建立基于测试不确定的扩展多信号流模型,可用一个六元组进行表述,即(F,T,E,PF,PT,C),具体构成如下:
(1)m+1维系统故障模式集F={f 0,f 1,…,f m},其中 f 0表示系统无故障状态;
(2)n维系统测试集T={t1,t2,…,tn};
(3)E=F ×T,其中,“×”号表示集合F与集合T的笛卡儿乘积,E表示故障与测试之间的拓扑连接关系;
(5)测试不确定概率集合 PT={(pd ij,p f aij)}(i=1,2,…,m;j=1,2,…,n),其中,pd ij=p(tj=1|f i=1),pf a ij=p(tj=1|f i=0),pd ij、pf a ij分别表示测试t j对故障模式 f i的检测概率和虚警概率;
(6)n维向量C=(c1,c2,…,cn),表示测试代价。
除此之外,由多信号流图模型经可达性算法[10]可以得到如下两个矩阵:
(1)测试确定条件下系统故障-测试相关性矩阵 FT,FT=[ftij](m+1)×n,其中

(2)测试不确定条件下系统故障-测试相关性矩阵 FTP=[ftp ij]m×n,其中
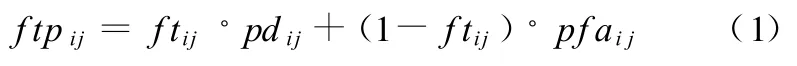
本文首先建立基于贝叶斯网络的测试性分析模型,并结合扩展的多信号流模型,通过贝叶斯网络参数学习过程来计算PT并以此获取f tp ij。
1.2 基于贝叶斯网络的测试性分析模型
1988年,Pearl[12]提出了贝叶斯网络的概念,它基于概率推理,本身就是一种不确定性因果关联模型。由于贝叶斯网络对于解决复杂系统不确定因素引起的故障分析具有很大的优势,在许多领域得到了很好的应用[13-14]。
在测试性分析中,如果将多信号流模型中的故障与测试看作节点,那么多信号流模型和贝叶斯网络在结构上很相似。由此可以根据系统多信号流模型构建面向系统测试性分析的贝叶斯网络B(G,P),如图1所示。它由两部分组成:
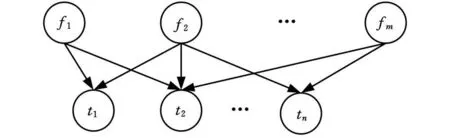
图1 面向系统测试性分析的贝叶斯网络模型
(1)具有M个节点的有向无环图G(V,E),用于表示贝叶斯网络结构。图1中的节点V={V1,V2,…,V M}=F∪ T={f 1,f 2,…,f m,t1,t2,…,tn}代表随机变量,fi(i=1,2,…,m)(正常/故障)表示第i个故障模式,tj(j=1,2,…,n)(通过/不通过)表示第 j个测试,记 f i、tj的第k(k=1,2)个取值分别为fki,tk
j。而节点间的有向边E代表故障节点与测试节点间相互关联关系。值得一提的是,该有向图蕴含了条件独立性假设:图中每个节点 Vi条件独立于由Vi的父节点pa(Vi)给定的非Vi后代节点构成的任何节点子集A(Vi),即
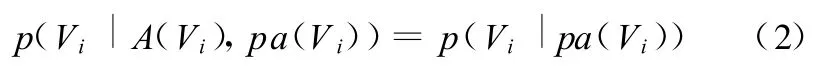
(2)与每个节点相关的条件概率表(conditional probabilities table,CPT),它表达了节点与其父节点之间的相关关系——条件概率。
由于具备了节点及其相互关系、条件概率表,故贝叶斯网络可表达网络中所有节点的联合概率,即

1.3 贝叶斯网络参数学习
根据构成,贝叶斯网络学习分为两部分内容:网络结构G的学习和条件概率表CPT的学习。根据装备多信号流图模型,测试领域专家可以通过一定的转换规则获得相应的贝叶斯网络结构。而要直接给出众多变量的CPT则非常困难,且随着系统复杂性增加,难度增大。因此在故障测试与诊断领域中,学习CPT更具有实际意义。
对于CPT参数学习问题的研究已有一些成功的方法和结果[12,15]。由于贝叶斯网络本质上是变量的联合概率分布的图形表示,故CPT学习可以归结为统计学中的参数估计问题。通常学习方法可以分为两大类:一是基于经典统计学的学习,采用频率方法,学习目标是寻找参数的点估计,如最大似然(maximum likelihood,ML)或最大后验概率(maximize a posterior,MAP);二是基于贝叶斯统计学的学习,采用贝叶斯方法,参数可以处理为其他任何随机变量,学习与推理是一样的。
对于图1所示的面向系统测试性分析的贝叶斯网络模型,假设:DI={CI f1,CI f2,…,CI fm,CIt1,CIt2,…,CItn}为故障与测试数据样本,元素CI fi(i=1,2,…,m)或CI ti(i=1,2,…,n)为样本DI的一个事例。对于本文所述问题而言,pa i(pa i∈F)为结构G中测试变量ti(ti∈T)的父节点集,并记其可能取值的数目为qi,γij表示pa i的第j个取值,则表示给定pai为第j种取值时,节点ti为第k种取值的概率,记为θij k。
贝叶斯网络参数学习的目标是基于网络拓扑结构G和训练样本集DI,利用先验知识,确定贝叶斯网络模型各节点处的条件概率密度,记为p(θ|DI,G),根据贝叶斯规则便可得到如下估计:

至此便可以获得图1所示网络的条件概率表,然后根据式(1)计算对应装备系统在不确定测试条件下的故障-测试相关性矩阵FTP。
2 测试性指标分析计算
测试选择的目的是在满足系统测试性参数指标要求前提下选择合理的测试项目组合,使测试代价最小[2]。下面首先基于不确定条件下的故障-测试相关性矩阵对测试性参数进行分析计算。
(1)故障检测率。对于故障 f i(f i∈F),在所选择的测试集Ts条件下,其能被检测到的概率为可通过贝叶斯推理得到。那么故障检测率形式化表示为

(2)关键故障检测率。对于关键故障f i(f i∈F),在所选择的测试集 T s条件下,其能被检测到的概率为1),可通过贝叶斯推理得到。那么关键故障检测率形式化表示为

(3)故障隔离率。由于存在一个测试可用于检测多个故障以及一个故障可被多个测试观测到的情况,因此故障隔离问题要远比故障检测问题复杂。若故障 f i和f j(f i,f j∈F且i≠j)可以被隔离,则必须满足矩阵FT第i行FT i与其第j行FTj相异。设Tfi为能检测故障fi的所有测试组成的集合,Tf j为能检测故障f j的所有测试组成的集合,那么 f i能被隔离的条件是:Tf i⊕Tf j≠0,∀f j∈F,f i≠f j。其中“⊕”表示集合异或,当两个集合不同时,结果为1。反之,故障 fi和f j位于同一模糊组的条件是:Tfi⊕Tfj=0,∀f j∈F,f i≠f j。如定义另一个运算符“⊙”表示两个集合的同或,即当 Tfi⊕Tfj=0时,Tfi⊙Tf j=1,表示故障 f i和f j属于同一模糊组。设所选择的测试集T s能隔离的所有故障构成的集合为F I,若给定故障隔离模糊度L,则有

对于任意 fi∈FI,设其能被隔离的概率可通过贝叶斯推理所得。由此可以获得故障隔离率形式化表示:
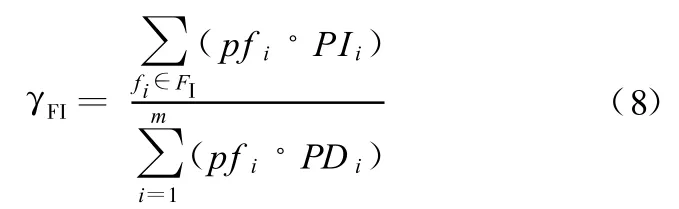
(4)虚警率。设故障 f i(f i∈F)对应可能产生的虚警概率为那么总的虚警率可以形式化表示为
3 基于HBPSOGA的测试优化选择
3.1 优化模型描述
根据测试选择目标及约束,通过测试性参数指标分析与计算过程,可以得到测试优化选择模型如下:

其中,FDR、FIR、FAR分别为给定的故障检测率、故障隔离率和虚警率。
3.2 基于HBPSOGA的测试优化选择算法
文献[6]将二进制粒子群算法(binary particle swam optimization,BPSO)与遗传算法(genetic algorithm,GA)相结合,提出混合二进制粒子群-遗传算法(HBPSOGA)进行测试确定条件下的测试优化选择,通过性能互补,既能通过GA避免陷入早熟收敛和局部最优,又能充分利用BPSO增强搜索速度,提高成功率。本文利用HBPSOGA对式(10)所示的测试不确定条件下的测试选择优化模型进行求解。首先假设:
(2)NP为当前迭代次数,Nmax为最大迭代次数,w为惯性权重,则w=w max-N P(w maxw min)/N max;
(3)c1、c2为加速因子,均为正实数为随机产生的一个介于(0,1)之间的正实数;
那么在BPSO中,位置与速度的更新公式如下:

而遗传算法作为一个较成熟的进化算法,以适应度为依据,通过对群体中的个体进行选择、交叉、变异等遗传操作算子实现群体内个体结构重组并不断迭代获得最优个体。结合两者优点,提出基于 HBPSOGA的测试优化选择,步骤描述如下:
(1)参数初始化,包括种群规模Popsize,遗传交叉概率P c、遗传变异概率P m,粒子群惯性因子w,学习因子 c1、c2,最大速度 v max和迭代次数N max。
(2)种群初始化,根据求解问题维数随机产生初始种群Pop=(xij)Popsize×n,其中n为所求问题的维数,即备选测试数目,当测试tj被选中时,xij=1,否则x ij=0,并定义适应度函数为

其中 ,D 、α、β 、γ、φ均为常数 。
(3)计算Pop中个体适应度并进行评价,采用轮盘赌方法选择两个个体,并以概率Pc两两进行交叉操作,得到种群Pop′。
(4)对Pop′中的个体以概率P m进行变异操作,得到种群 Pop″。
(5)对Pop″中的个体进行适应度评估,得到个体最优位置Pbest和全局最优位置Gbest,并按照式(11)和式(12)分别对种群速度和位置进行更新,产生下一代种群Pop。
(6)若迭代次数已经达到最大次数,则算法结束,输出最优个体作为问题最优解;否则转(3)。
4 案例验证
表1为某系统[6]故障与可选测试间对应关系。系统共有15个故障源,20个可用测试,表2是故障的先验概率,表 3是各测试对应的测试费用。

表1 某系统故障与测试故障对应关系

表2 故障先验概率

表3 测试费用 美元
由系统故障与测试相关关系,根据1.2节所述便可建立相应的贝叶斯网络模型,如图2所示。由于贝叶斯网络参数学习需要大量的训练样本,且本文重点研究系统在不确定信息条件下的测试选择问题,因此鉴于篇幅所限,略去贝叶斯网络参数学习过程。假设条件概率仿真数据如表4所示。

图2 系统贝叶斯网络图
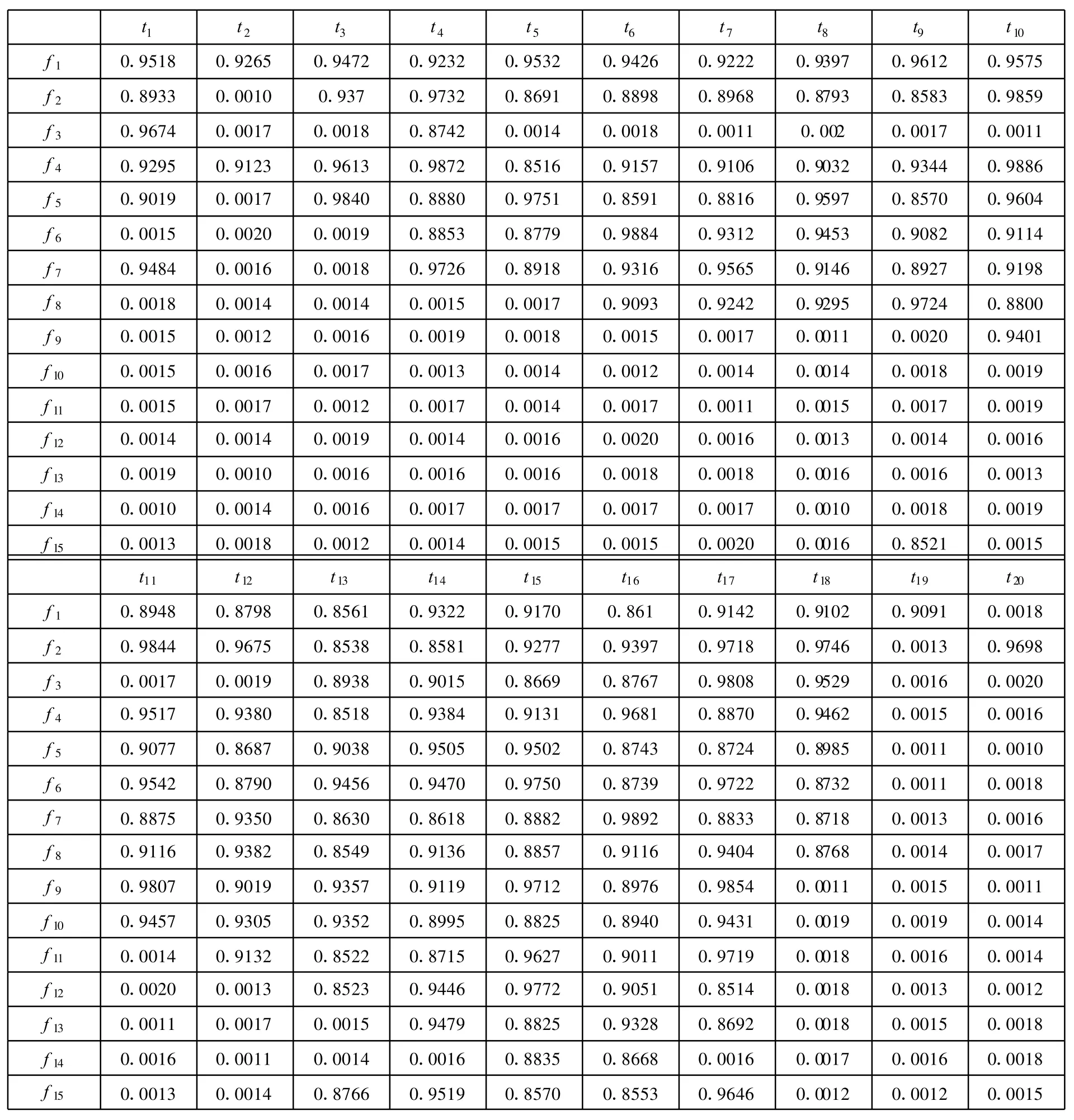
表4 故障-测试CPT
设系统测试性设计的要求为:故障检测率不低于90%,故障隔离率不低于80%,关键故障{f 4,f 5,f 6,f 7,f 10,f 11,f 14,f 15}检测率为100%,虚警率不大于3%,且费用最小。利用HBPSOGA对文献[6]与本文所述问题分别进行测试优化选择,参数设置均为:Popsize=60,p c=0.8,p m=0.02,wmax=0.9,wmin=0.4,Nmax=200,c1=c2=1.4962,D=10,α=β=γ=0.5,φ=50。计算结果对比如表6所示。
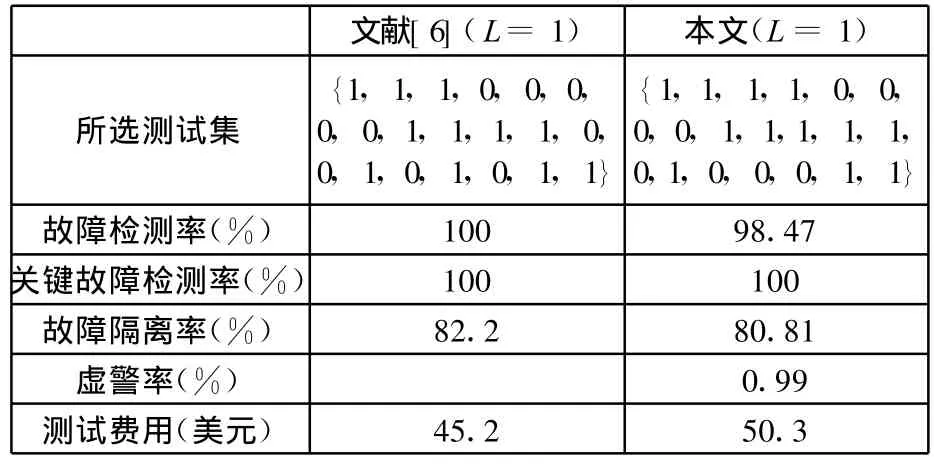
表6 本文与文献[6]结论对比
结果分析:从表6可以看出,测试优化选择结论随着测试性分析方法的不同而发生相应的变化。通过以上对比,利用本文方法进行测试性分析及测试优化选择具有两个特点:①本文所得结果虽然使得测试性指标有所降低,但依然能够满足既定要求;②由于考虑了装备测试过程中的不确定性,其分析更加符合实际情况,这也是提出本文方法的重要目的。
5 结束语
随着装备功能结构与运行环境越来越复杂,测试过程中普遍存在大量不确定信息。本文基于贝叶斯网络建立测试性分析与评估模型,通过计算测试性关键指标参数,建立了测试优化选择模型。在此基础上利用 HBPSOGA对备选测试项目进行优化。案例分析表明,本文所提出的模型与方法表达的信息量高,具有处理不确定性信息的能力,使得测试性分析与评估结果更为客观,为复杂装备测试优化选择提供了可靠的依据,可有效指导测试性方案设计。
[1] Navy-EC.MIL-STD-2165-1985 Testability Program For Electronic Systems and Equipments[S].Washington D C:Department of Defense,1985.
[2] 田仲,石君友.系统测试性设计分析与验证[M].北京:北京航空航天大学出版社,2003.
[3] 龙兵.多信号建模与故障诊断方法及其在航天器中的应用研究[D].哈尔滨:哈尔滨工业大学,2005.
[4] 吕晓明,黄考利,连光耀.基于混沌遗传算法的测试选择优化问题研究[J].弹箭与制导学报,2009,29(3):265-269.
[5] 杨成林,田书林,龙兵.多值故障字典的测点选择与序测试设计[J].系统工程与电子技术,2009,31(9):2271-2275.
[6] 陈希祥,邱静,刘冠军.基于混合二进制粒子群-遗传算法的测试优化选择研究[J].仪器仪表学报,2009,30(8):1674-1680.
[7] DSI International Inc.eXpress[EB/OL].[2010-07-26].http://www.dsiintl/WebLogic/products.aspx.
[8] Qualtech Systems Inc.Testability,Engineering and Maintenance System(TEAMS)[EB/OL].[2010-07-26].http://www.teamqsi.com/press/2000/teams_pr2.htm.
[9] Raghavan V,Shakeri M,Pattipati K R.Test Sequencing Algorithms with Unreliable Tests[J].IEEE Transactions on SMC-part A:Systems and Humans,1999,29(4):347-357.
[10] Sui R,Yunkai Z,Feili Y,et.al.Dynamic Multiplefault Diagnosis with Imperfect Tests[J].IEEE Transactions on Systems,Man and Cybernetics,Part A:Systems and Humans,2009,39(6):1224-1236.
[11] Deb S,Pattipati K R,Raghavan V,et al.Multi-signal Flow Graphs:a Novel Approach for System Testability Analysis and Fault Diagnosis[C]//Autotestcon'94 IEEE Systems Readiness Technology Conference.Anaheim,1994:361-373.
[12] Pearl J.Probabilistic Reasoning in Intelligent Systems:Networks of Plausible Inference[M].San Francisco:Morgan Kaufmann,1988.
[13] Esteves RM,Wlodarczyk T W,Chunming R,et al.Bayesian Networks for Fault Detection Under Lack of Historical Data[C]//2009 10th International Symposium on Pervasive Systems,Algorithms,and Networks(ISPAN).Kaohsiung,2009:732-736.
[14] 李俭川.贝叶斯网络故障诊断与维修决策方法及应用研究[D].长沙:国防科学技术大学,2002.
[15] 张少中,杨南海,王秀坤.贝叶斯网络参数的在线学习算法及应用[J].小型微型计算机系统,2004,25(10):1799-1801.

