航空公司不安全事件发生率的贴近度研究

王永刚，何士笑

（中国民航大学安全科学与工程学院，天津 300300）

航空公司不安全事件发生率的贴近度研究

王永刚，何士笑

（中国民航大学安全科学与工程学院，天津 300300）

运用模糊数学中的Euclid贴近度方法，分析了中国民航2005—2009年各航空公司在各季度的亿吨公里不安全事件发生率数据，确定出航空公司各季度发生不安全事件的贴近关系为相邻季度的不安全事件发生率贴近度最大，且有第四季度不安全事件发生率与第三季度最贴近，第一季度与上一年第四季度不安全事件发生率的贴近度次之，之后依次是第二季度与第一季度、第三季度与第二季度。随着贴近度的变小，各季度与相邻前一季度不安全事件发生率的可比性变差。

安全管理；不安全事件；贴近度；航空公司；趋势分析

航空公司经常进行安全趋势分析和对比，以及准确地把握其内部安全运行动态，如近几年发生严重事故征候的趋势比较，每月轮胎轧伤不安全事件的趋势比较等。多数的趋势分析都采用下一时间段与相邻上一时间段的数据进行比较，而不管统计期限是短还是长。对于统计期限较长的单位，如季度，由于时间间隔较长，数据波动较大，前后相邻阶段发生不安全事件的数量差异比较大，数据间就可能不具有良好的可比性，如果将贴近关系不大的数据进行比较，其结果会产生较大偏差或波动，进而对安全趋势的合理判断产生不良影响，因此对该类数据进行趋势预测或分析前应首先进行可比性论证。

本文通过分析历年来各季度不安全事件发生率之间贴近度大小，得出季度不安全事件统计数据的差异及可比关系，最后对结论进行了验证。

1 Euclid贴近度方法适用性的验证

民航法规的不断完善使各类不安全事件的标准不断发生变化，导致收集的数据存在一定差异；而不安全事件上报及收集过程中人为归类的主观判断，导致统计数据存在不确定性，因此本文欲将所要研究的不安全事件发生率贴近情况采用模糊数学中Euclid贴近度确定。贴近度是指模糊集合之间的靠近程度，设 X={x1，x2，…，xn}，A、B∈F（X），则 A、B 间 Euclid 贴近度为[1-2]

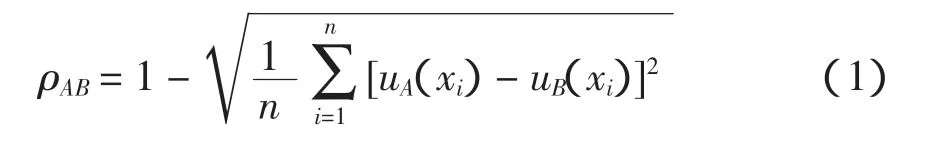
其有如下性质：ρAB=ρBA（对称性），即A相似于B的程度与B相似于A的程度是一样的。假设各月、各季度的不安全事件发生率共组成了n个模糊集U1，U2，…，Un，取

为确定该方法对于判断航空公司不安全事件发生率贴近度的适用性，笔者采用较小统计单位——月

份的相关数据进行了验证。为克服由于运输飞机数量变化、运输架次变化等原因引起分析数据的波动，本文采用了比值而不是绝对值来表示；为使分析结论具有普遍适用性，本文收集了近5年国内航空公司各月份不安全事件数量和周转量数据[3－7]并进行了处理，即以不安全事件数目/总周转量——亿吨公里不安全事件发生率进行分析，每个月构成的模糊集如下

为简略起见，选取具有代表性的6个模糊集合进行分析：X4、X5、X8、X9、X10、X11，根据式（1）和式（2），各个月模糊集合之间的距离为

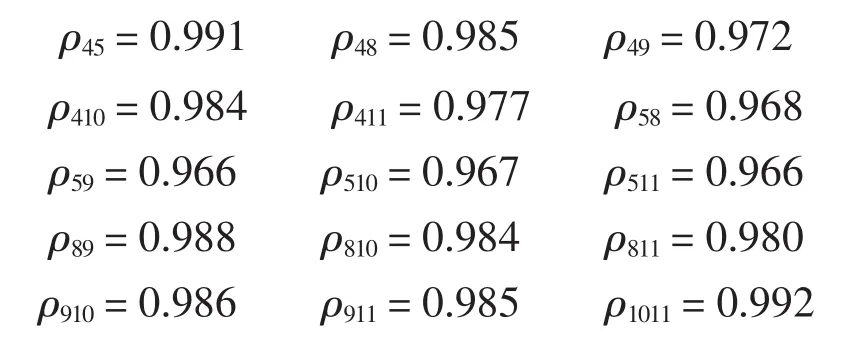
各月份模糊集合之间的贴近度关系分别为

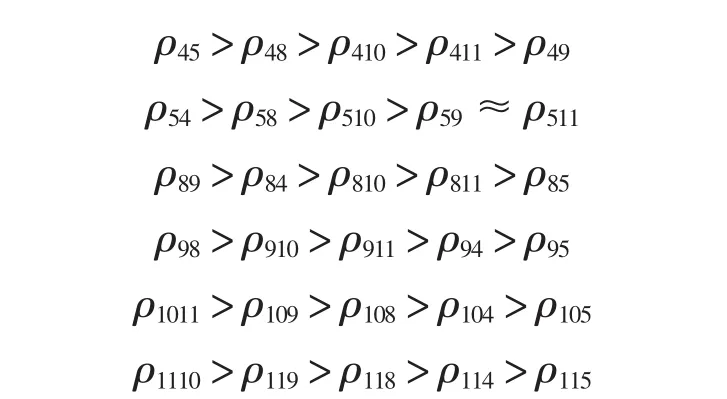
由上述各贴近度关系，得出如下结论：相邻月份之间发生不安全事件的贴近度最大，且各相邻月份在贴近程度上差异非常小——仅从0.001～0.006，几乎可以忽略。

由上可知，运用模糊数学理论中的Euclid贴近度方法，可以比较合理地判断出模糊集合间的贴近关系。

2 季度不安全事件发生率的贴近关系判定

季度趋势是以一个季度数据为单位进行的比较，笔者欲探究各季度不安全事件发生率之间的关系，故以国内各航空公司各季度亿吨公里不安全事件率为分析对象[3－7]，具体如表 1 所示。

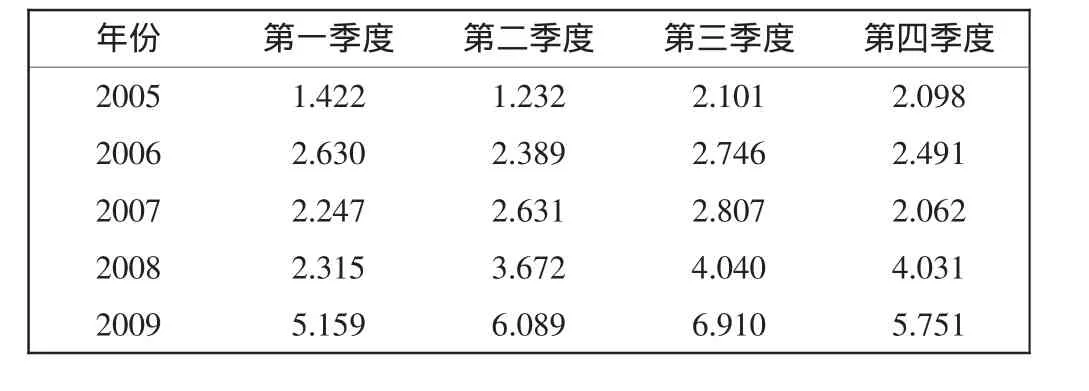
表1 2005—2009年各季度亿吨公里不安全事件发生率Tab.1 Occurrence of unsafe events per 100 million ton-km in each quarter from 2005—2009

根据式（1）、式（2），可计算出各季度不安全事件发生率的贴近度

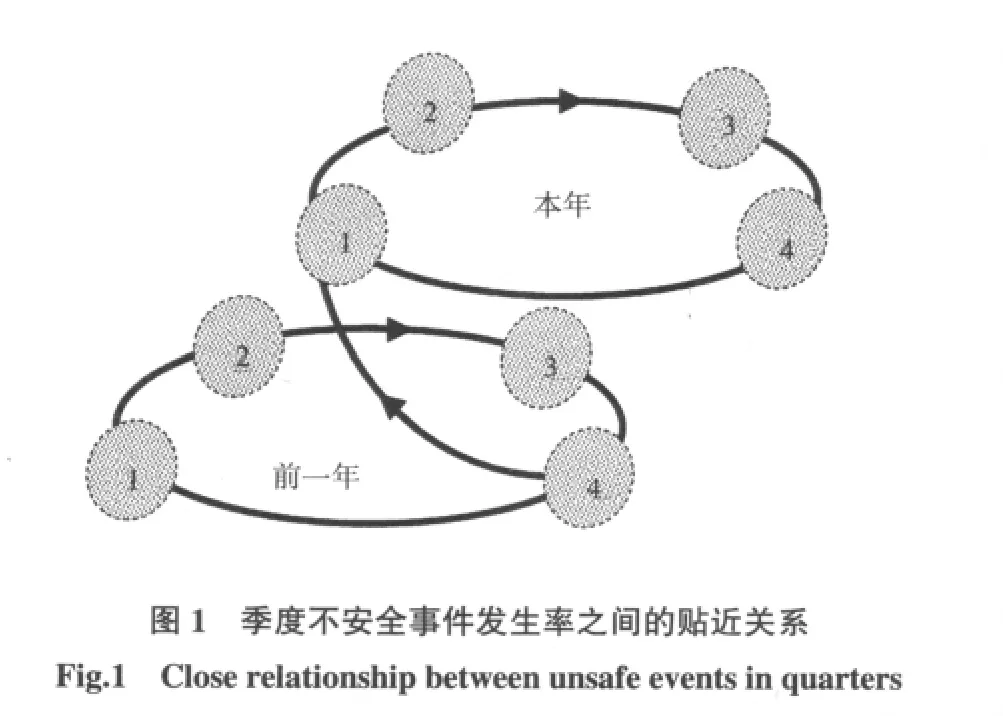
由以上计算结果可知，ρ43＞ ρ14＞ ρ21＞ ρ32＞ ρ42＞ρ14＞ρ13。根据模糊集合Euclid贴近度的相关性质，可用图1来表示各季度不安全事件发生率的相互位置关系。

笔者得出如下结论：①各个季度之间发生不安全事件的贴近度是不相同的；②相邻季度的贴近度最大，且其相似程度差异较大（从0.002到0.02）：第三季度不安全事件发生率与第四季度最贴近，第一季度与上一年第四季度不安全事件发生率的贴近度次之，之后是第一、二季度和第二、三季度。由于贴近度越大集合中的数据越靠近，可比性越好，在数据比较过程中波动性就越小、越稳定，相应地其比较的结果就越准确。

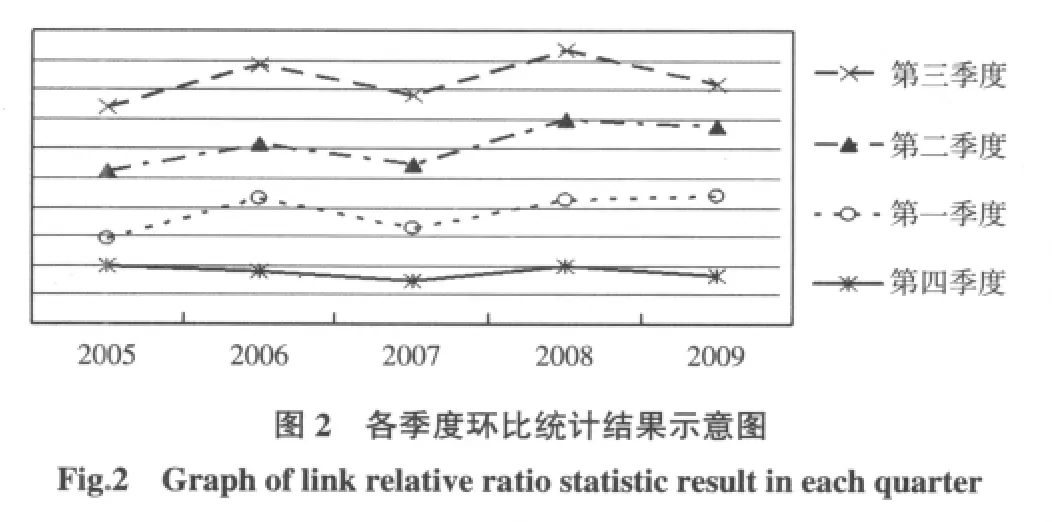
为了清楚地展现各季度与其前一相邻季度不安全事件比较结果的波动情况，在伸缩比例相同的前提下，将各季度的折线分别向上平移，如图2所示。从图2中可以看出，第四季度与第三季度不安全事件发生率比值的统计结果波动最小、最稳定；而第三季度与第二季度比值的波动最大，稳定性最差。与上述相邻季度贴近度的结论相一致。

比较相邻月份的贴近度与相邻季度的贴近度数值可知，随着民航不安全事件统计时限的变长，相邻统计单位之间的贴近度差异变大，并非每个相邻单位之间的可比性都一样好。

3 结语

本文通过分析国内各航空公司在近5年的亿吨公里不安全事件发生率数据，得出如下结论：

1）模糊数学理论中的Euclid贴近度能准确合理地判定出民航各种安全数据的贴近程度，可为确定比较对象提供依据。

2）航空公司各季度亿吨公里不安全事件发生率的贴近关系为第三、四季度发生不安全事件的差异性最小，贴近度最高，可比性最好；其次是第一季度不安全事件发生率与上一年第四季度；之后依次是第一、二季度和第二、三季度。

3）欲比较的单位（如月度、季度）不具有周期变化规律时，单位时间越长，各相邻单位间的贴近度差异就越大，可比性差异越明显。

[1] 彭祖赠，孙韫玉.模糊数学及其应用[M].武汉：武汉大学出版社，2007.

[2] 丁 星.根据Euclid贴近度研究考试成绩排序的特点[J].系统工程理论及实践，1996（9）：103-106.

[3] 张志中.从统计看民航2005[M].北京：中国民用航空总局规划科技司，2005.

[4] 张志中.从统计看民航2006[M].北京：中国民用航空总局规划科技司，2006.

[5] 王战斌.从统计看民航2007[M].北京：中国民用航空总局规划科技司，2007.

[6] 王战斌.从统计看民航2008[M].北京：中国民用航空总局规划科技司，2008.

[7]CAAC.中国民用航空安全信息网[EB/OL].[2010-06-17].http：//safety.caac.gov.cn/.2005-2009.

Close-Degree Study of Unsafe Event Ratio for Airlines

WANG Yong-gang，HE Shi-xiao
（College of Safety Science&Engineering，CAUC，Tianjin 300300，China）

Implying the method of Euclid close-degree in fuzzy mathematics， the paper determines out the close-degree of the airlines′unsafe events in each quarter by analyzing the domestic occurrence of unsafe events per 100 million ton-km in four quarters from the year 2005—2009.From the result， we can conclude that the closestdegree is the quarters neighborhood，the unsafe occurrence of the forth quarter and the third quarter is the closest， successively is the first quarter and the forth in last year， the second quarter and the first quarter， the third quarter and the second one.As the close-degree becoming smaller，the comparability is growing worse.

safety management；unsafe event；close-degree；airlines；trend analysis

X924.3

A

1674－5590（2011）01－0039－03

2010-06-20；

2010-10-26

王永刚（1963—），男，天津人，教授，博士，研究方向为民航安全管理体系（SMS）、民航风险管理、人为因素等.

（责任编辑：杨媛媛）