二重积分中值点渐近性的讨论

郭 辉，谭 艳

（重庆师范大学数学学院，重庆 401331）

讨论积分中值定理中值点的渐近性的文献很多，文献［1］最早讨论第一中值定理，文献［2］讨论积分第二中值定理的中值点渐近性，文献［3］总结了积分第一、二中值定理的中值点的渐近性，并得出了一些比文献［1］更强的结果.文献［4］讨论了最简单的二重积分中值定理中值点的渐近性.

这些文献中，没有人讨论含两个函数的二重积分中值定理中值点的渐近性.此处就这方面进行了研究，定义二重积分中值定理的正则中值点（ζx，ηy）并讨论它的渐近性.

1 积分中值点的渐近性

1.1 一元积分中值点的渐近性

积分第一中值定理中值点的渐近线在文献［2］［3］［5］［6］［7］中已经给予了讨论，在这里先归纳一元函数第一积分中值定理中值点ζ渐近性的一些结论.

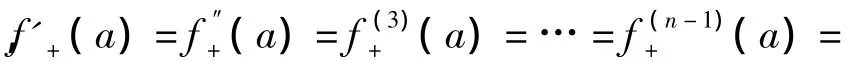
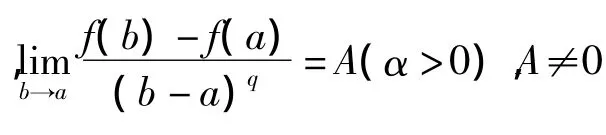
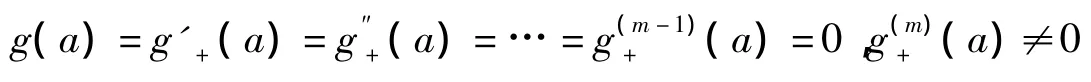
特别地，得到积分第一中值定理中值点ζ的渐近性的一个简单推论.

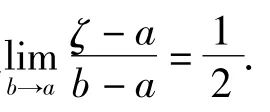
2 二元积分第二中值定理中值点的渐近性

在文献［2］［3］［8］中都对一元函数积分第二中值定理中值点的渐近性进行了讨论，而文献［4］［9］在文献［2］［3］［8］的基础上对二重积分中值定理中值点的渐近性进行了讨论，并得到二重积分正则中值点（ζx，ηy）的定义如下:

定义 1［4］设函数f（x，y）在区域Dxy={（u，v）|a≤u≤x，b≤v≤y}上连续，函数g（x，y）在Dxy连续且不变号，则至少存在一点（ζx，ηy）∈Dxy，使得:

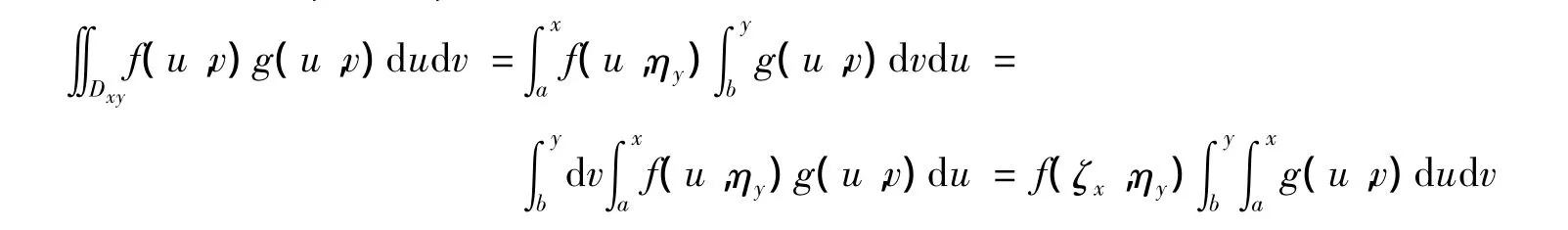
则称（ζx，ηy）为正则中值点.

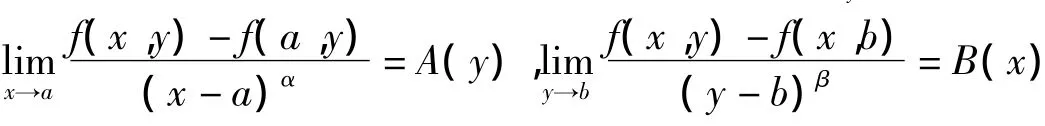
由洛必达法可知:

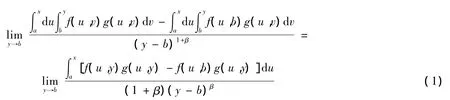
又因为函数f（u，v），g（u，v）在矩形区域Dxy={（u，v）|a≤u≤x，b≤v≤y}上都连续，所以式子（1）中的积分和极限可以交换次序，即:

另一方面，对于任一确定点y（y≠b），x→a时，同理可得:

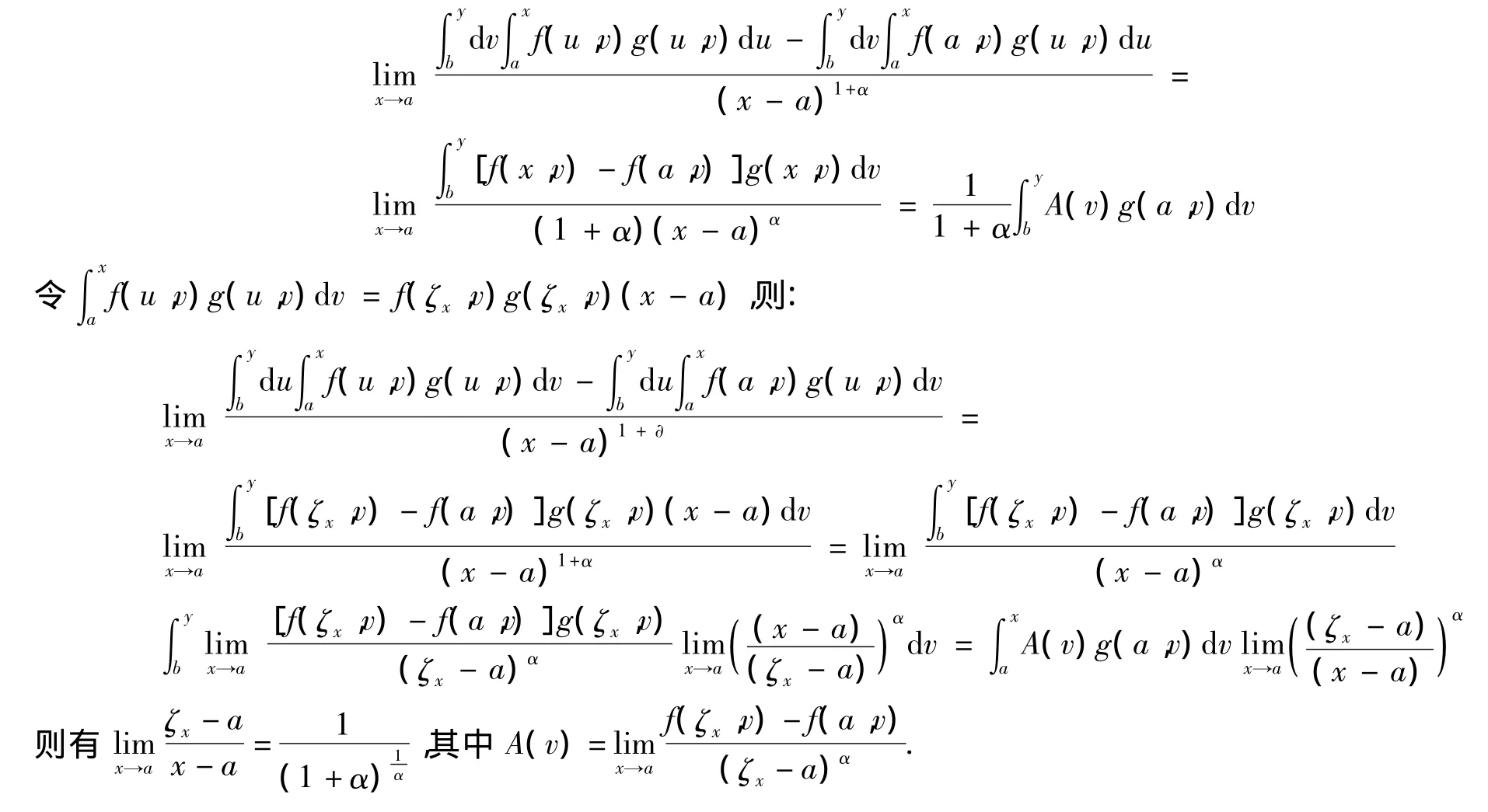
3 结论

对二重积分中值定理中值点的渐近性进行了讨论.通过比较，二重积分中值定理中值点渐近性的一些结论完全可以由一元函数中值点渐近性推广得到.此处二元函数中值点渐近性的一些简单结论是否可以推广到多元函数中值点渐近性的讨论，有待进一步研究，但其方法很具有参考意义.

［1］BERNARD JACOBSON.On the Mean Value Theorem for Integrals［J］.Amer Math Monthly，1982，89:300-301

［2］郑权.关于第二积分中值定理的中值点ξ的渐近性质［J］.大学数学，2005（6）:113-115

［3］郑权.积分第一、二中值定理的中间点的渐近性质的一般性定理［J］.数学实践与认识，2005，35（5）:240-243

［4］蔡文康.二重积分中值定理中值点的渐近性［J］.上海电力学院学报，2005（1）:90-92

［5］邵品琮.关于积分第一中值定理［J］.曲阜师范学报:自然科学版，1979，2（5）:12-15

［6］刘一鸣.关于积分第一中值定理的证明［J］.曲阜师范学报，1980，2（6）:56-58

［7］王成伟，张晓燕.第一积分中值定理中间点的渐进性［J］.北京服装学院学报，2000（4）:23-24

［8］唐金菊.积分第二中值定理中的渐进性［J］.芜湖职业技术学院报，2001，2（3）:38-40

［9］杨彩萍.二重积分中值定理中间点的进一步讨论［J］.中国民航学报，2000（1）:57-61