基于角度细分的永磁电机矢量控制的研究

熊丽满 白连平

（北京信息科技大学自动化学院，北京 100192）

1 引言

随着永磁材料、电力电子技术及控制理论的发展，永磁同步电机得到迅速发展，其中，电压空间矢量脉宽调制(SVPWM)就是一种很好地应用于交流电动机数字化控制的方法，该方法具有谐波含量少、开关损耗小、直流电压利用率高等优点，从而降低了PMSM的转矩脉动，提高了交流调速性能。因此建立永磁同步电机矢量控制模型是十分必要的，由于带有高分辨率位置传感器的永磁同步电动机成本高，所以本文中采用低分辨率的位置传感器以及软件算法估算出转子的实际角度。主要是根据位置区间的平均速度及平均加速度原理来实现位置估算，从而得到高分辨率转子位置信号。

2 永磁同步电机的数学模型

永磁同步电机在d-q坐标系基本方程如下[3]

电压方程：

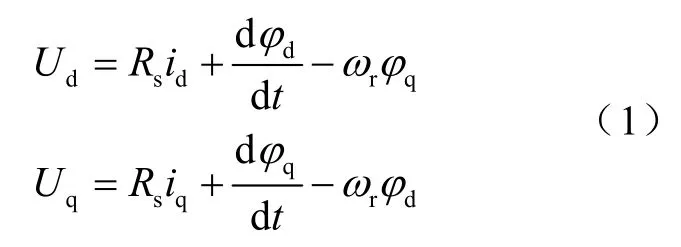
磁链方程：

电磁转矩方程：

机械运动方程：

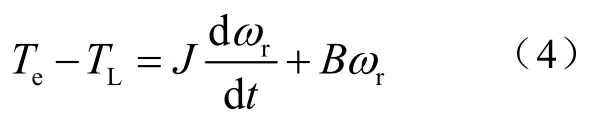
3 PMSM转子磁场定向控制原理

三相永磁同步电机的模型是一个多变量、非线性、强耦合系统，为了实现转矩线性化控制，就必须要对转矩的控制参数实现解耦。通常采用转子磁场定向控制方法，图1给出PMSM转子磁场定向控制原理。

图1 系统控制框图

首先，通过霍尔位置传感器出来的低分辨位置信号,再根据位置估算算法得到高分辨率位置信号θ，最终转化为转子的电角度θ和角速度ω，将给定角速度与实测角速度ω的偏差作为速度调节器（PI）的输入，速度PI控制器的输出作为定子q轴电流的参考值，定子三相电流需经过Clark变换、Park变换到dq旋转坐标系中,再与参考输入qrefi 和drefi 相比较，采用dref0i = 控制策略。通过电流调节器（PI）分别控制交直轴电流,从而控制电机的转矩和磁场，控制信号再经Park逆变换,通过SVPWM算法模块产生6路PWM信号控制逆变器电路的输出，最终达到控制电机转速和转矩，构成永磁同步电机闭环控制系统。

4 矢量控制的仿真研究

4.1 位置信号产生

本文在低分辨位置信号的基础上，结合软件算法估算出转子高分辨率位置信号，三相霍尔位置信号相隔120°安装在电机中，当电机转动时，产生相位相差120°的方波信号，在此方波基础上结合DSP相位检测功能得到低分辨位置信号。首先分析角度细分的原理，再在Sinmulink环境下建立估算转子位置模型，产生高分辨位置信号，为实验研究提供参考。

由于霍尔位置传感器每个周期只提供6个位置信号，不能直接满足永磁同步电机矢量控制，因此需要利用6个低分辨率的位置信号得到高分辨率的转子位置信号。

当电机稳态运行时，可以用前60°位置区间的平均速度 1iω-来估算当前区间的转子的位置角度imθ，从图中可以看出当前的转子位置 imθ等于低分辨位置信号 iθ加上由iθ已旋转的角度 ikθ，其计算公式为

式中，sT为采样周期，k为t到it的采样周期次数。

图2 转子位置估算示意图

由于实际中电机转速在某一段不是匀速的，那么估算高分辨位置信号可能超出区间的最大值，需要对角度进行校正，假设一个60°区间为（iθ，i+1θ），那么，若，则令，若在新的霍尔区间到来时，估算位置信号，则强制令。

在DSP中实现高分辨位置的估算，根据霍尔位置传感器提供的低分辨位置信号，结合DSP相位检测捕捉电平跳变，可以得到六个低分辨位置信号，霍尔位置信号与转子位置信号对应关系如表1所示，在捕捉电平跳变时，产生捕捉中断，在捕捉中断中确定低分辨位置信号，同时开启0.1ms定时中断，除此之外，还需要一个定时器测量每个60°时间间隔，这样，0.1ms内转子转过的角度增量θΔ，就可以确定，当一个定时0.1ms中断到来时，根据，计算高分辨位置信号角度。

根据表达式（5）和（6），建立高分辨位置信号仿真模型，并得到转子角度θ仿真波形。

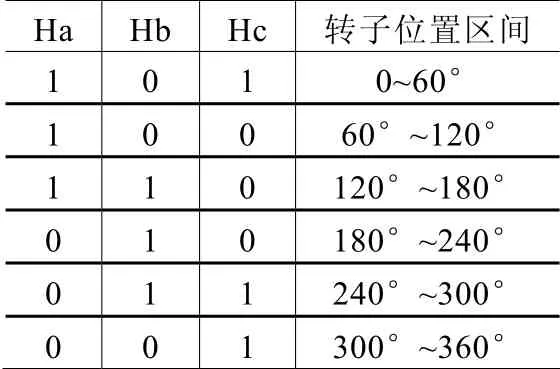
表1 霍尔位置信号与转子位置对应关系

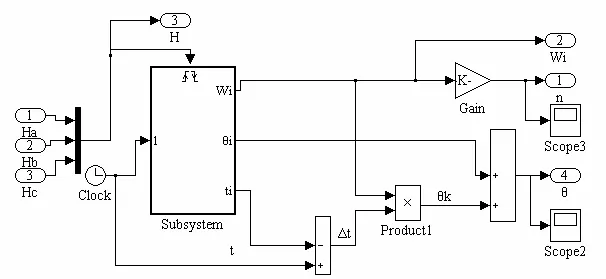
图3 高分辨率位置信号产生

4.2 坐标变换模块

矢量控制中用到的变换有：将三相平面坐标系向两相平面直角坐标系的转换（Clarke变换）和将两相静止直角坐标系向两相旋转直角坐标系的变换（Park变换）。

Clark变换的表达式为

Park变换以及Park逆变换的表达式

4.3 SVPWM仿真模型

理论上， SVPWM以三相对称正弦波电压供电时,交流电机产生的理想圆形磁链轨迹为基准,用逆变器不同的开关模式产生的实际磁通去逼近基准磁链圆,从而达到较高的控制性能。由于逆变器产生的矢量数目有限,不能产生角度连续变化的空间矢量，SVPWM方法通过8个基本空间矢量中两个相邻的有效矢量及零矢量,并根据各自作用时间不同,来等效电机所需的空间电压矢量 outU ,其原理图如图4所示[7]。

（1）扇区判断

首先定义三个变量 ref1V 、ref2V 、ref3V ，令它们与Uα、Uβ的关系为

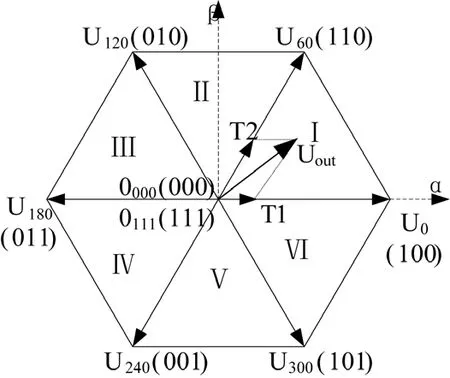
图4 基本电压空间矢量

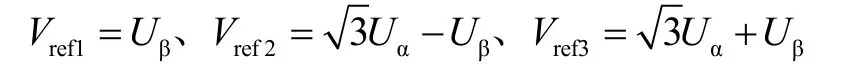
另外再定义三个变量A、B、C，根据αU和 βU的关系，当ref10V ＞ ，令A=1，否则令A=0，当ref20V ＞ ，令B=1，否则令B=0，当ref30V ＜ ，令C=1，否则令C=0，取N=A+2B+4C。且 N与扇区号成一定对应关系，其关系如表2所示。

表2 N与扇区号sector的对应关系

（2）计算X、Y、Z和T1、T2

图5 T1、T2的数学模型

（3）确定矢量切换点

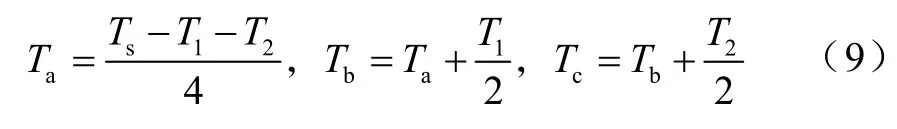
由上式计算出aT、bT、cT，再根据空间矢量调制原理，将 aT、bT、cT分配给Tcm1，Tcm2，Tcm3[1]，这样就可以得到不同扇区内空间矢量的占空比，再由占空比和等腰三角波比较产生对称的空间矢量PWM，最终产生6路PWM脉宽调制信号。

综上所述，实现SVPWM算法的整体模型如图6所示。

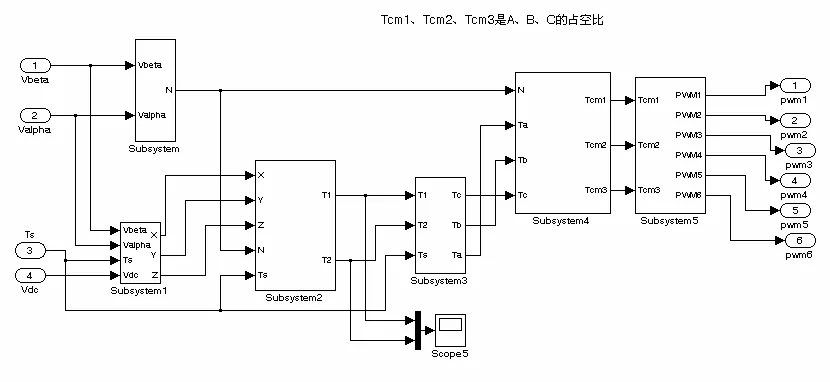
图6 SVPWM算法实现

5 实验研究

本文中采用DSP56F803控制芯片，设计整个系统的硬件电路以及编写矢量控制算法，并在永磁同步电机调试运行。系统硬件电路包括系统控制电路、IGBT驱动电路、逆变电路、电流检测电路、位置信号检测电路、电源电路、键盘电路等。图7为系统硬件框图。

图7 硬件框图

整个系统软件部分由主程序和中断服务子程序组成，在主程序中完成系统的初始化工作，在中断程序中执行系统的功能模块程序。系统初始化完成后进入循环等待状态，直到有中断到来，执行相应的中断服务函数。主要的中断函数有输入捕捉中断、定时中断、测速中断、PWM重载中断、A/D转换完成中断以及键盘中断等，根据系统要求设置中断优先级，使控制芯片各个模块能正常运行。

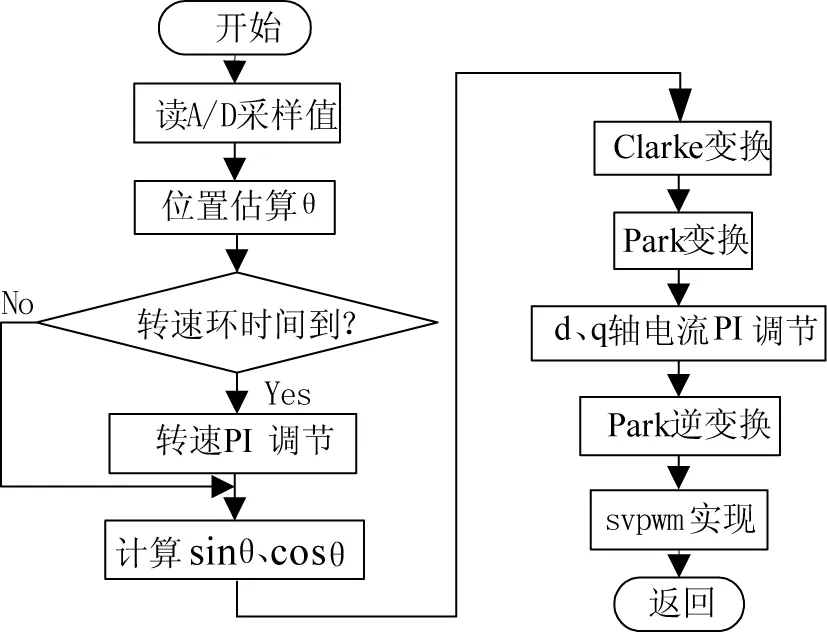
图8 0.1ms定时中断流程图

系统主要算法、位置估算以及PI控制都是在0.1ms定时中断完成，所以给出 0.1ms中断的流程图，如图8所示。

由于位置估计是建立在对离散霍尔位置信号时间间隔的计算，在启动阶段，速度偏低，定时计算器可能溢出，造成估算结果不准确，即不能正确反应转子当前位置，所以采用直流方波起动电动机，待电机运行稳定后，再切换到矢量控制，解决了永磁同步电机在低速脉动大而造成失步的问题[4]。

6 仿真与实验结果

本文永磁同步电动机的基本参数：额定功率2.2kW，额定电压220V，额定电流8.3A，额定转速2000r/min，极对数 mp=4，定子绕组电阻R=0.29Ω，转化为d-q轴的转子电感为Ld=Lq=8.5mH，每极磁通量Φ=0.175 Wb，转子的转动惯量

为了验证模型的正确性和有效性，对模型进行仿真实验，给定角速度为50×pi（rad/s）（即1500r/min），采样频率为0.0001s，直流母线电压，电机带负载起动，仿真时间设置为0.2s，电机带5N·m负载起动，得到定子的三相电流、转速波形以及角度θ仿真图形。

图9 定子三相电流

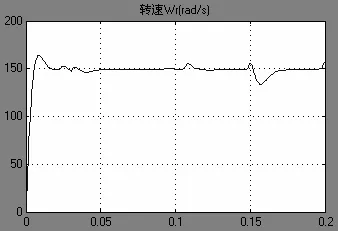
图10 转速波形

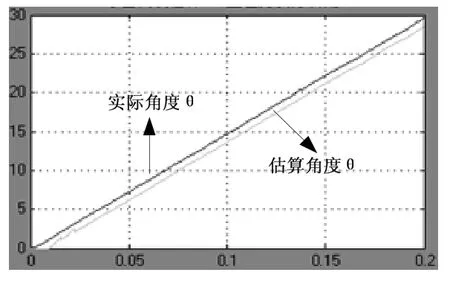
图11 转子角度θ仿真图形

实验研究结果：DSP56F803开发环境中集成了一套十分有特色的可视化调试工具PC Master，它能够实时的显示和记录实验中的波形和数据，给实验研究带来很大的方便，当电机上电运行，通过PC Master监测到的转子角度θ（theta）变量的变化，如图12所示，图中角度是标幺化后的值，即（-1～1）表示实际角度为(π～π)- 。用示波器采集的其中一相电流波形如图13所示。

图12 实际转子角度

图13 相电流波形

7 结论

仿真图形结果表明，永磁同步电机矢量控制系统的具有稳定动态性能，仿真为实验研究提供了参考，具有一定的实际意义。从图12和图13说明，实际中电机运行较平滑，转子的位置信号好，故采用角度细分方法获得高分辨位置信号是可行，可以把它作为检测转子的实际位置，实验结果与仿真结果相符合，验证了基于角度细分在永磁同步电机矢量控制上的应用是可以实现的。

[1] 何亚屏,年晓红.永磁同步电机矢量控制Matlab仿真研究[J].变流技术与电力牵引,2007(6)：58-62.

[2] 唐任远等.现代永磁电机理论与设计[M].北京.机械工业出版社,1997.

[3] 林海.基于DSP的永磁同步电机控制方法的研究[D].西北工业大学,2007.3.

[4] 房森林,章跃进.基于离散位置信号的永磁同步电机矢量控制[J].微特电机,2010,38(7).

[5] 黄忠霖，黄京.控制系统Matlab计算及仿真[M].北京：国防工业出版社，2009.

[6] 董窈窈.采用低分辨率位置传感器的正弦波永磁同步电机控制系统[D].山东大学.2007.4.

[7] 王巍等.一种永磁同步电机控制系统仿真建模的研究[J].沈阳工程学院学报(自然科学版),2008,4(1).

[8] 王晶菡,李铁才,杜坤梅.基于Matlab的永磁同步电机控制系统仿真研究[J].宁波职业技术学院学报,2007,11(2).

[9] 许振伟.基于低分辨率传感器的PMSM伺服系统[J].电工技术学报,2004,19(10).

[10] 邹继斌，徐永向等.正弦波无刷直流电机的新型转子位置检测方法[J].中国电机工程学报,2002,22(12).