群体决策信息获取激励的相容性研究

卢光松

（安徽建筑工业学院 管理学院，合肥 230022）

0 引言

群体决策在现代社会无处不在。群体可以利用各群体成员所掌握的与决策问题相关的信息，与个体相比，更有可能发现世界的真实状态，因而更有可能作出正确的决策。不考虑其它因素，仅从信息集结的角度看，让更多拥有信息的个体参与决策可以改善决策质量，这种观点符合人们的直觉，其形式化证明出自18世纪Condorcet给出的陪审团定理。该定理认为：群体决策可以有效集结信息，在多数决定规则下，增加群体成员数量可以增加作出正确决策的概率，并且随着成员数量趋于无穷，作出正确决策的概率趋于1。

Condorcet陪审团定理及其后来的很多拓展往往都有个潜在的假设：群体决策者所掌握的与决策问题相关的信息是事前外部给定的，或是以零成本获得的［1］。但对于许多现实决策情形，信息并不是不需要投入成本和努力就能轻易得到的，如审稿专家需要付出一定的时间和精力才能决定稿件是否符合录用标准，因此决策者必须决定是否付出以及付出多少代价以获取信息。而在群体决策中，与决策问题相关的信息是公共物品，因而存在典型的所谓社会惰化现象或搭便车问题。文［1］对陪审团决策中的信息获取问题进行了研究，认为陪审员的信息准确程度取决于陪审团的大小，更大的陪审团的陪审员具有更少的动机认真听取审判过程，所以更大的陪审团作出正确判决的概率可能更小，从而导致陪审团定理不再成立。文［2～8］进一步研究了群体决策中的理性无知（rational ignorance）问题，对仍能有效集结信息时信息获取成本或成本函数需要满足的条件进行了分析，这些文献针对多数决定规则，假定所有群体成员具有完全相同的决策偏好。其中文［2,4,5,6］证明，当全体或部分群体成员的信息获取成本函数在获取零信息处的二阶导数为零，则Condorcet陪审团定理仍然有效。

文［9］证明，采用适当保守的决策规则可以促进群体成员收集证据，从而改善决策质量。文［10,11］对存在信息获取时的群体决策最优规则与最优群体成员数进行了研究，文［10］指出，在只考虑单调纯策略均衡的条件下，除非群体成员的信息足够准确，否则一致性规则或接近于一致性规则的规则不可能最优；文［11］认为，事前最优的决策机制事后可能不是最优的。前述文献都假定决策群体成员具有相同的偏好，而文［12］分析了偏好差异对信息获取的影响，证明获取较多信息的成员也可能弃权，成员获取的信息量与其弃权的概率不一定负相关。文［13,14］的研究结论为避免信息获取中的搭便车问题从决策群体人员组成方面提供了理论参考，指出具有极端偏好的成员相对来说更具有收集高成本信息的动机，但这两篇文献所研究的不属于严格意义上群体决策，因为其中的委员会成员仅负责收集与报告信息，自身并没有决策权。另外，文［15］通过一个仅有两个成员的群体决策模型，指出群体成员间的交流可能会恶化信息获取中的搭便车问题。

现实中的群体决策者一般存在决策偏好差异，而且决策信息的获取对不同的决策者一般需要不同的成本，这里的“成本”差异来自于两个方面：一方面不同的决策者获取相同质量的信息需要投入的时间、精力和金钱等可能不一样，如审稿专家对稿件涉及领域的熟悉程度不同导致审稿需要花费的时间不同；另一方面相同的投入对不同的决策者往往具有不同的负效用。本文假定群体决策者具有不同的先验知识、偏好与信息获取成本，针对确定性单调决策规则，分析决策者的先验知识、偏好与信息获取成本对其信息获取动机的影响。

1 模型描述

由n个成员所组成的决策群体N={1，2，…，n}面临一个二分决策问题，需要通过投票表决的方式集体选择一个决策选项 d∈{a，b}，世界的真实状态为 ω∈{A，B}，各成员从最终决策中获得的效用取决于世界的真实状态ω，但ω的取值在投票表决时对于群体成员而言是未知的。

成员i∈N关于真实状态ω取值为A的先验概率记作Pi（ω=A）=πi，于是状态为 B 的先验概率是 Pi（ω=B）=1-πi，状态ω的两种取值对于所有群体成员都是先验可能的，即0＜πi＜1，∀i∈N。在状态ω，如果群体最终决策为d，则成员i获得的效用为ui（d，ω），各成员间的偏好差异体现为效用函数值的不同。 这里假设 Δui（A）=ui（a，A）-ui（b，A）≥0 且 Δui（B）=ui（b，B）-ui（a，B）≥0，∀i∈N，也即在状态 A（B），所有成员都倾向于采取决策a（b），因而不存在极端偏好者。各成员的先验概率与偏好信息都是私密的。

每个成员i∈N在投票表决前可以获得一个与世界真实状态相关的私有信息 si∈{α，β}，P（α|A）=P（Si=α|ω=A）=P（β|B）=P（Si=β|ω=B）=q，∀i∈N，其中 0.5＜q＜1，私有信息的质量q反映了私有信息与真实状态的相关程度。此处的假设有如下局限性：首先，所有群体成员获取的信息质量相同（在其它文献中往往也理解为群体成员的决策能力相同），都是q，事实上群体成员私有信息的质量不可能完全相同，因此在理想情况下，应该根据群体成员信息的相对质量对其投票进行加权处理，但很明显，对群体成员的投票进行加权处理在现实中既缺乏技术上的可操作性，也缺乏社会上的可接受性。其次，在不同的真实状态，投入相同的成本，所获取的信息与真实状态的相关性相同，这与现实情况不相符，例如，证明犯罪嫌疑人有罪和无罪的难度是不一样的，因此更合理的假设应该是：P（Si=α|ω=A）=q1，P（si=β|ω=B）=q2，但这样做除了使公式表示更复杂化外，数学推导过程并没有本质改变，对文章结论的现实意义也没有实质性影响。

信息的获取需要付出一定的成本，成员i的信息获取成本为ci≥0，该成本对成员意味着负效用。信息获取过程中成本的投入对外界来说是不可观测的，因此外界无法通过有效的惩罚措施强制群体成员获取信息，成员是否获取信息完全出于自身效用最大化的考虑。另外，给定世界的真实状态，各成员获得的信息相互之间条件独立。

确定性单调决策规则是现实中最为广泛采用且最具有可操作性的群体投票表决规则，因此本文的分析针对确定性单调决策规则：在n个成员中至少 m（m为［1，n］内的整数）个成员投票选择a，则群体最终决策d=a，否则决策d=b。本文假设群体成员在投票表决前不存在信息的相互交流，且投票表决是同时进行的或是匿名的，因而不需考虑投票过程中的所谓从众行为。

2 博弈分析

每个成员根据自己的先验概率、偏好与信息获取成本决定是否获取信息以及如何投票表决，成员i∈N的策略记为σi（πi，ui，ci）=（λ，vα，vβ），其中 λ∈{0，1}为成员 i的信息获取策略，λ=0表示该成员不获取信息，λ=1表示获取信息，vα∈{a，b}为成员 i获取的信息 si=α 时的投票选择，vβ∈{a，b}为获取的信息si=β时的投票选择。如果成员i不获取信息，则vα=vβ。因为本文讨论的是所有群体成员都获取信息为Nash均衡，成员的偏好和信息获取成本等需要满足的条件，所以仅需考虑纯策略。同时，这里认为群体成员所采取的策略仅取决于自身的先验概率、偏好与信息获取成本，和成员的具体身份无关，即只考虑对称策略：σi=σ，∀i∈N。

从成员i的角度看，如果所有其他成员所使用的策略都是σ，将任一成员j∈N/{i}在真实状态为ω时投票选择a的概率记作 Pj（a|ω，σ），简写为 Pj（a|ω），则对于阈值为 m 的确定性单调决策规则，在状态ω，成员i投票选择a，群体决策结果为a的概率是：

式中的vi为成员i的投票选择。

在状态ω，成员i投票选择b，则群体决策结果为a的概率是：

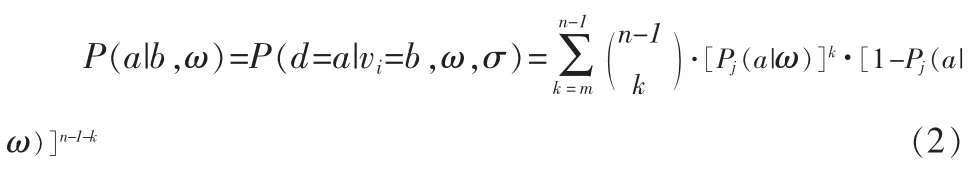
假设成员i获取信息，如果获得的信息si=α，则其投票选择α将得到的期望效用是（不考虑信息获取成本）：

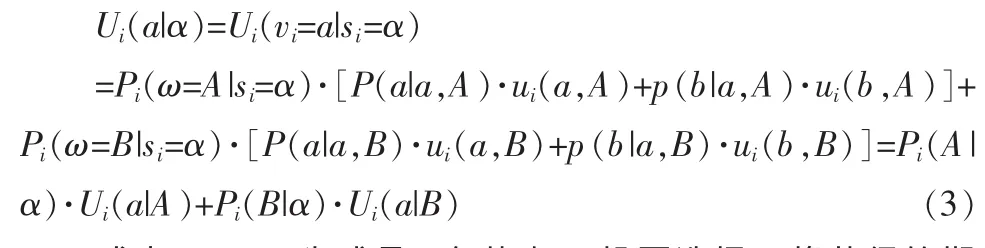
式中Ui（d|ω）为成员i在状态ω投票选择d将获得的期望效用。

如果成员i获得的信息si=β，则其投票选择b将得到的期望效用是：

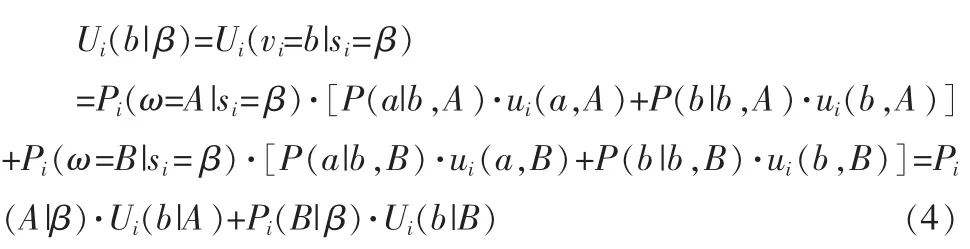
于是，在所有其他成员都采取策略σ的前提下，如果成员i获取信息，且获得的信息si=α则投票选择a，si=β则投票选择 b，即采取策略 σi=（1，a，b），成员 i将获得的期望效用为（计入信息获取成本ci）：

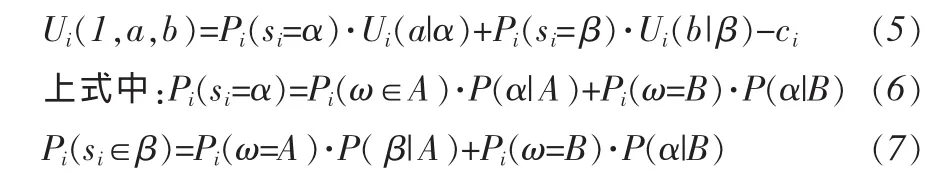
如果成员i不获取信息，总是投票选择a，即采取策略σi=（0，a，a），将获得的期望效用为：

如果成员i不获取信息，总是投票选择b，即采取策略σi=（0，b，b），将获得的期望效用为：

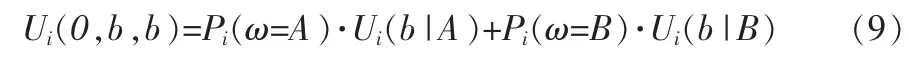
在所有其他成员都采取策略σ的前提下，根据式（3）～（8），可得成员 i采取策略（1，a，b）与采取策略（0，a，a）的期望效用之差为：

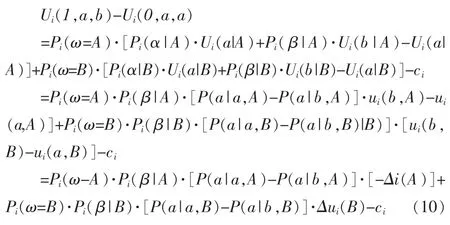
根据式（1）与（2）可得：

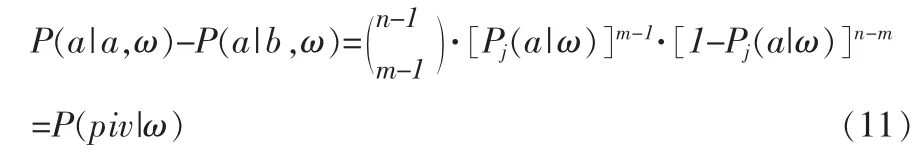
上式中的piv是指成员i的投票选择对最终决策结果具有决定性影响（to be pivotal）的事件，P（piv|ω）是指在状态ω，成员i的投票选择可以改变群体决策结果的概率。

于是，式（10）可以改写为：

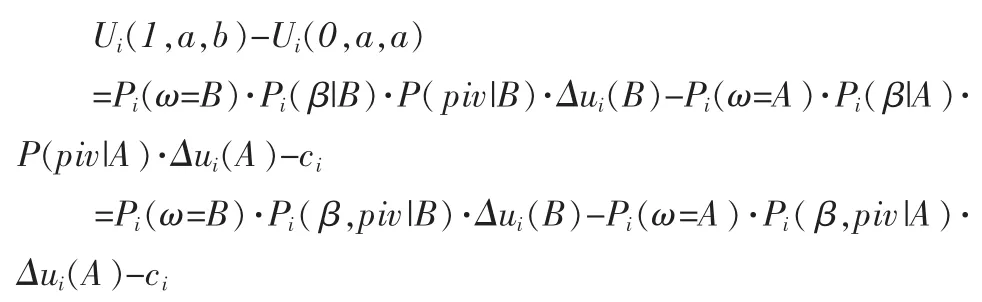
（此处推导是因为模型假设：给定世界的真实状态，各成员获得的信息相互之间条件独立。）

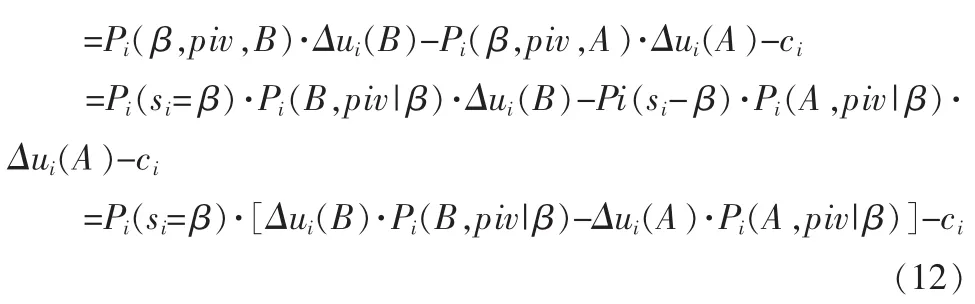
上式中的 Pi（ω，piv|β）为成员 i获得信息 β 后判断状态是 ω 且自身为 piv 的概率，Δui（B）·Pi（B，piv|β）可理解为成员i获得信息β后，从投票选择a改为投票选择b将得到的期望效用，Δui（A）·Pi（A，piv|β）可理解为成员 i获得信息 β 后，从投票选择a改为选择b将损失的期望效用。因此，在所有其他成员采取策略σ的前提下，对于成员i来说，如果其付出代价获取信息，能够获得信息β的概率乘以获得信息β后投票选择b的好处，若该乘积值大于信息获取成本，则成员倾向于采取策略（1，a，b）而不是策略（0，a，a）。

同理可得，在所有其他成员都采取策略σ的前提下，成员 i采取策略（1，a，b）与采取策略（0，b，b）的期望效用之差为：

在所有其他成员采取策略σ的前提下，对于成员i来说，如果其付出代价获取信息，能够获得信息α的概率乘以获得信息α后投票选择a的好处，若该乘积值大于信息获取成本，则成员倾向于采取策略（1，a，b）而不是策略（0，b，b）。

3 信息获取均衡条件

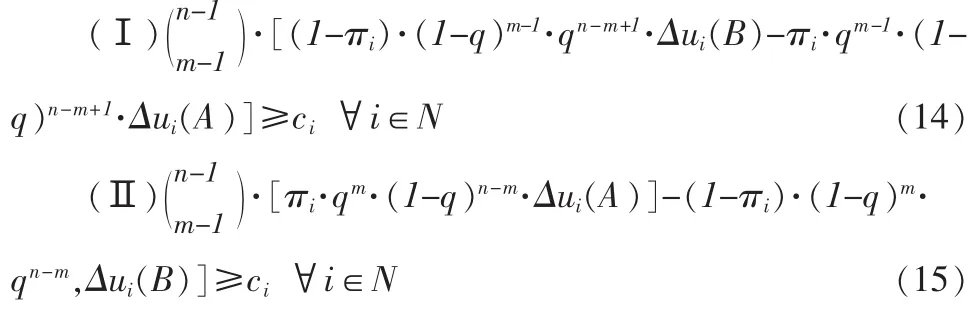
定理1给定决策群体成员数n、阈值为m的确定性单调决策规则以及决策问题的信息质量q，所有群体成员都获取信息为Nash均衡，成员的先验概率πi、效用函数ui与信息获取成本ci需要满足的条件是：

证明：首先，任一成员若获取信息，则其一定采取策略（1，a，b）。这是因为如果该成员总是投票选择a或总是投票选择b，则其不需要付出代价获取信息，另外由模型定义，在状态 A（B）所有成员都倾向于采取决策 a（b），故策略（1，b，a）不符合理性原则。因此，群体成员可能采取的策略为（1，a，b）、（0，a，a）或（0，b，b）。

某成员 j采取策略（1，a，b），则该成员在状态 ω 投票选择a的概率等于在状态ω获得信息α的概率，即：

根据式（10）与（11）可得，在其他成员都采取策略（1，a，b）的前提下，对于成员 i，策略（1，a，b）不劣于（0，a，a）的必要条件是不等式（14）。 同理，策略（1，a，b）不劣于（0，b，b）的必要条件是不等式（15）。定理得证。

由不等式（14）与（15）可以看出，在其他成员都采取策略（1，a，b），即都获取信息且按信息投票的前提下，先验概率的值过于接近0或1都可能使得成员不愿获取信息，因此，具有极端偏见的成员相对来说缺少收集高成本信息的动机。

需要指出的是，本文描述的群体决策博弈存在多个Nash均衡。如所有成员都不获取信息且总是投票选择a对于阈值m＜n的确定性单调决策规则是Nash均衡，因为这时任何一个成员改变策略都对决策结果没有影响。因此，即使定理1的条件满足，所有群体成员都获取信息仅是多个可能的Nash均衡中的一个。但如果将不等式（14）与（15）中的等号去掉，则得到所有群体成员都获取信息为优势策略均衡的充分必要条件。

4 结论

对于多数决策问题，为了作出正确的决策，决策者必须付出一定的代价获取信息以识别世界的真实状态。但在群体决策中，与决策问题相关的信息是公共物品，因此存在典型的社会惰化现象或搭便车问题。随着群体成员的增多，单个成员能够影响最终决策的可能性减小，因而具有更少的动机参与信息的收集，进而可能引起群体决策质量的下降。本文假定群体决策者具有不同的先验知识、偏好与信息获取成本，首先针对确定性单调决策规则分析了决策者的信息获取与投票表决策略，然后给出了所有决策者都获取信息为激励相容时，决策者的先验知识、偏好与信息获取成本需要满足的条件。

虽然本文的问题描述具有较为普遍的应用背景，但本文与此领域的类似文献一样没能给出具体的实例分析。这主要是因为利用博弈论研究群体决策问题的文献一般以完全理性假设作为判断与决策的微观基础，例如假定所有群体成员严格按照贝叶斯规则更新自己的信念等，从而限制了研究成果在现实中的直接可验证性。尽管博弈论研究文献的完全理性假设对于心理学家和普通人来说都是难以接受的，但博弈论文献还是以其数学分析的简洁与严谨颠覆了很多直觉上的认识。利用博弈论作为理论工具分析决策群体成员的动机和理性行为，有助于我们理解决策机制的哪些方面可能会引起不利于决策目标实现的策略性行为，进而有助于决策机制的改进。本文针对实践中最常用的确定性单调决策规则，分析了群体决策者的先验知识（可理解为偏见）、偏好与信息获取成本对其信息获取动机的影响，相关结论对于群体决策规则设计、决策成员人选等具有一定的参考价值。

[1]Mukhopadhaya K.Jury Size and the Free Rider Problem[J].The Journal of Law,Economics,and Organization，2003，（19）.

[2]Martinelli C.Would Rational Voters Acquire Costly Information?[J].Journal of Economic Theory，2006，129（1）.

[3]Martinelli C.Rational Ignorance and Voting Behavior[J].International Journal of Game Theory，2007，35（3）.

[4]Kitahara M,Sekiguchi Y.Condorcet’s Jury Theorem under Costly Information Acquisitio n[C].Working Paper,University of Tokyo,2004.

[5]Kitahara M,Sekiguchi Y.Aggregate Accuracy under Majority Rule with Heterogeneous Cost Functions[J].Economics Bulletin，2006，4（25）.

[6]Kitahara M,Sekiguchi Y.Condorcet Jury Theorem or Rational Ignorance[J].Journal of Public Economic Theory，2008，10（2）.

[7]Bag P,Levine P,Spencer C.A Note on:Jury Size and the Free Rider Problem[J].Economics Bulletin，2006，4（3）.

[8]Triossi M.Costly Information Acquisition.Better to Toss a Coin?[C].Working Paper,Collegio Carlo Alberto,2010.

[9]Li H.A Theory of Conservatism[J].Journal of Political Economy,2001,109（3）.

[10]Nicola P.Committee Design with Endogenous Information[J].Review of Economic Studies，2004，71（1）.

[11]Gerardi D,Yariv L.Information Acquisition in Committees[J].Games and Economic Behavior，2008，62（2）.

[12]Oliveros S.Who Abstains in Equilibrium[C].Working Paper,U-niversity of California,Berkeley,2008.

[13]Beniers K,Swank O.On the Composition of Committees[J].Journal of Law,Economics,and Organization，2004，20（2）.

[14]Cai H.Costly Participation and Heterogeneous Preferences in Informational Committees[J].The RAND Journal of Economics，2009，40（1）.

[15]Swank O H,Wrasai P.Deliberation,Information Aggregation,and Collective Decision Making[C].Working Paper,Tinbergen Institute,2003.