基于SVPWM的永磁同步电动机控制系统的研究
张 萍
(江阴职业技术学院 电子信息工程系,江苏 江阴214405)
随着电子技术和控制技术的发展,永磁同步电动机(PMSM)的控制技术也日趋成熟,且在工业界得到了广泛的应用。采用空间矢量脉宽调制(SVPWM)算法控制PMSM,将在PMSM的三相定子绕组中产生正弦波电流,形成旋转磁场,使电动机按要求的速度运转。与直接的正弦脉宽调制(SPWM)技术相比,PMSM控制简单,数字化实现方便,且在电机线圈的电流中产生更少的谐波成分,降低了电机转矩的脉动,提高了对IGBT逆变桥直流供电电源的利用效率[1,2]。
1 PMSM控制系统的构成
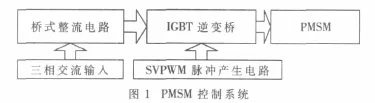
PMSM控制系统的构成如图1所示。三相交流输入经过二极管桥式整流电路整流之后得到直流电压,由DSP芯片产生的SVPWM脉冲控制IGBT逆变桥,并给IGBT逆变桥供电,从而在由逆变桥驱动的PMSM三相定子绕组中产生互差120°电角度的正弦波电流,形成等幅的旋转磁场,使电机按照一定的速度进行旋转。
1.1 IGBT逆变桥
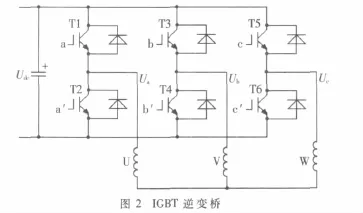
PMSM控制系统中的 IGBT逆变桥如图2所示,Ua、Ub和 Uc是其电压输出,T1~T6是 6个 IGBT,它们分别被 a,a′,b,b′,c 和 c′这 6 个来自 DSP 芯片的控制信号所控制,U、V和W分别为PMSM的定子三相绕组。当逆变桥上半部分的一个IGBT开通时,其下半部分相对应的 IGBT 应被关闭,即 a、b 或 c 为 1 时,则 a′、b′和 c′为0。a、b和 c为 0或为 1的状态, 决定了 T1~T6这 6个IGBT的开关状态,从而决定了 Ua、Ub和 Uc三相输出电压的波形情况。如果用SVPWM脉冲控制这6个IGBT的通和断,则PMSM的三相定子电流波形接近于理想的正弦波形,从而产生恒定角速度旋转的圆形磁场,使PMSM按指定的速度进行运转[3]。
由图2可得到逆变桥输出的相电压矢量与开关状态矢量的关系[1,4]如式(1)所示。
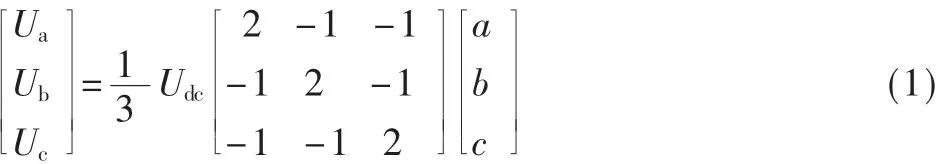
在(α,β)坐标系中,与相电压相对应的分量可以用式(2)表示:
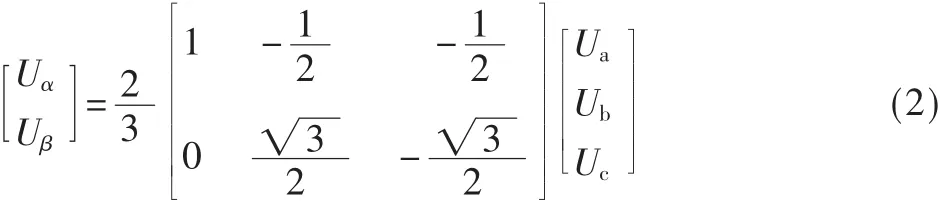
由于逆变桥中,6个IGBT的开关状态的组合一共有8种,即开关变量矢量[a b c]T共有8种取值,则相电压 Ua、Ub和 Uc及(α,β)坐标系中的 Uα和 Uβ也分别有 8种取值。8种开关组合决定了8个基本空间矢量,此8个基本空间矢量如图3所示。每相邻的两个基本空间矢量之间所包围的区域依次叫作 Sector 0~Sector 5,如图3所示。

1.2 SVPWM原理及算法实现
在图3中,将扇区Sector0的电压矢量Uout映射到基本向量 U0和 U60的边沿上,则有[5-7]:
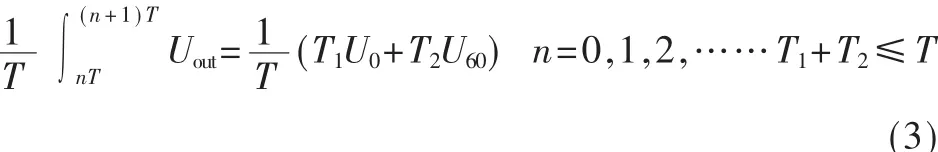
式(3)中,T表示一个 PWM周期时间长度,T1和 T2分别表示在一个周期时间T中基本空间矢量U0和U60各自的作用时间。T0是零矢量在一个周期中的作用时间,于是有等式:

当T极小时,式(3)可化成下式:

将 Uout映射到α和β轴上,则可以得到式(6):

由于所有基本空间矢量的幅值都为2Udc/3,则由式(6)可 得 到 式(7):
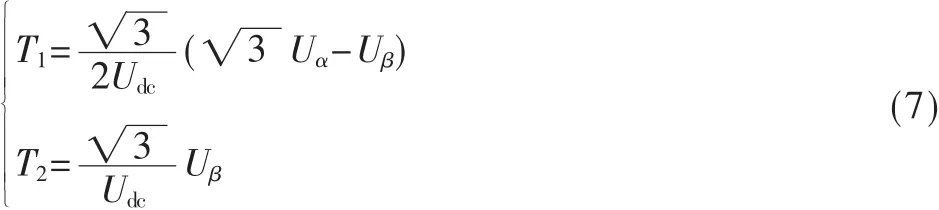
同理可求得其他扇区中基本空间矢量在一个PWM周期中的作用时间。如果定义式(8),则可以得到每个扇区中包围这个扇区的两个基本矢量在一个PWM周期中的作用时间[8,9],如表1所示。

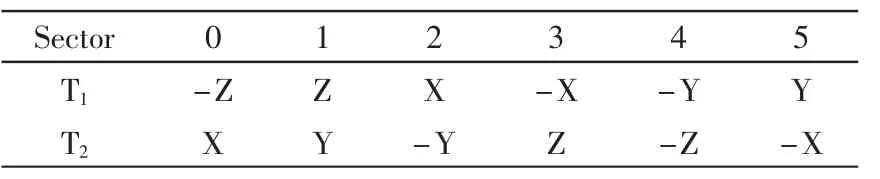
表1 T1和T2的取值
对于式(9),定义 3 个变量 a、b、c,如果 Vref1>0,则a=1,否则 a=0;如果 Vref2>0,则 b=1,否则 b=0;如果 Vref3>0,则 c=1,否则 c=0。 设 N=4×c+2×b+a,则很容易得到 N与扇区数Sector的对应关系。
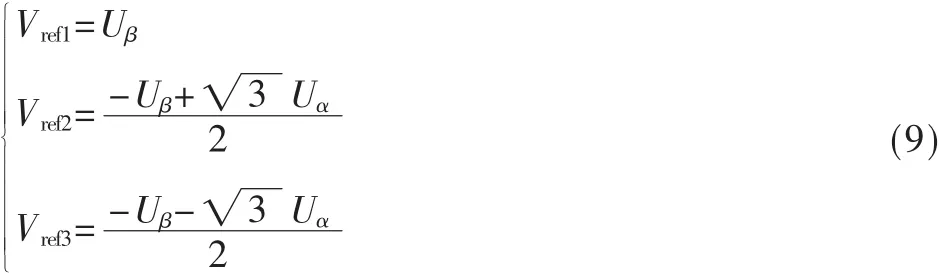
为了保证三相桥臂在一个PWM周期中导通的占空比,所应设置的比较值分别定义为 Tcm1、Tcm2和 Tcm3,并定义式(10),则 N与扇区数 Sector及 Tcm1、Tcm2和 Tcm3的关系如表2所示。

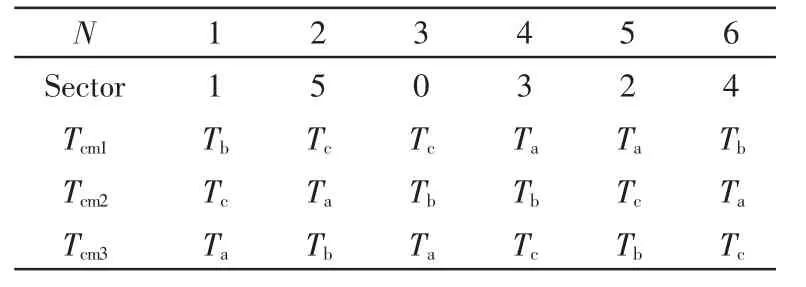
表2 N、Sector和 Tcm1、Tcm2、Tcm3的对应关系表
将 Tcm1、Tcm2、Tcm3与设置为连续增/减模式的 DSP 芯片定时器进行比较后得到PWM脉冲,控制图2中的三个桥臂的通断,从而在PMSM的三相定子绕组产生相位差为120°的正弦波形电流。
3 系统的Simulink仿真
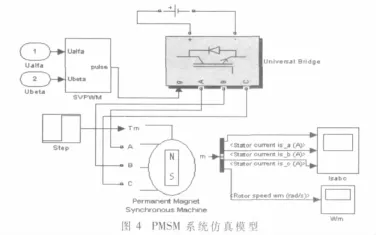
系统仿真模型[10,11]如图4所示。选取PMSM的参数为:电磁转矩 Te=0.8 N.m,额定电压 Udc=300 V,电机最高转速ωm=3 000 r/m。
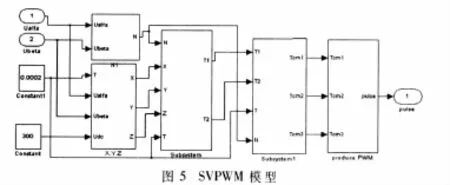
其中按照上述算法构建的SVPWM的Simulink仿真模型如图5所示。取 PWM周期为 200 μs,直流电源 Udc为300 V。
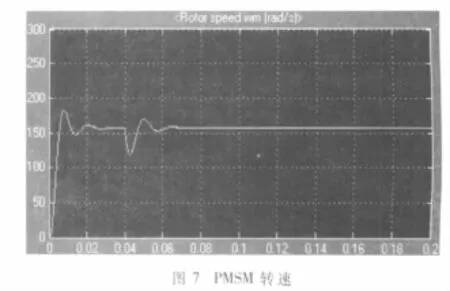
PMSM系统仿真模型运行后,得到定子A、B、C相绕组电流、电机转速如图6、图7所示。
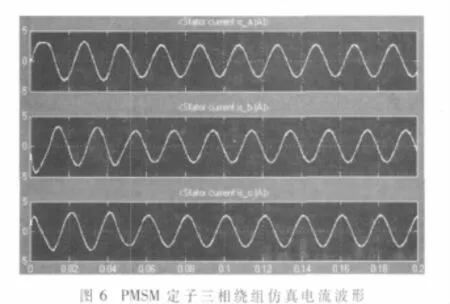
从仿真波形可以看出,定子绕组电流和电机转速除了在启动瞬间有较多的谐波成份外,迅速稳定之后波形还是比较理想的:定子三相绕组电流基本呈相位差为120°的正弦波形,电机转速基本稳定在 160 rad/s,即为160/(2pi)×60=1 528 r/m,与选定的电机参数完全一致。另外通过改变SVPWM脉冲频率可以方便地改变电机转速。
本文介绍了采用SVPWM脉冲控制永磁同步电动机的原理及其实现的过程,建立了系统的Simulink仿真模型,并对模型运行结果进行了分析。结果表明:采用SVPWM技术控制永磁同步电机是一种理想的控制方法,相较于其他的PWM调速方法,这种方法算法简单,定子绕组电流谐波成分少,直流电压利用率高,有着广阔的应用前景。
[1]刘和平,王维俊.TMS320LF240x DSP C语言开发应用[M].北京∶北京航空航天大学出版社,2002.
[2]BROECK H W.Analysis and realization of a pulsewidth modulation based on voltage space vector[J].IEEE Trans on IA,1998,24(1)∶142-150.
[3]邵群涛,徐余法.电机与拖动基础[M].北京∶机械工业出版社,2002.
[4]杨贵杰,孙力,崔乃政,等.空间矢量脉宽调制方法的研究[J].中国电机工程学报,2001,21(5)∶79-83.
[5]BLASKO V.Analysis of a hybrid PWM based on modified space-vector and triangle comparison methods[J].IEEE Trans on IA,1997,33(3)∶756-764.
[6]赵镜红,张俊洪,杨涛.基于 DSP的 SVPWM的研究[J].电机与控制学报,2002,6(2)∶108-110.
[7]熊健,康勇,陈坚,等.电压空间矢量调制与常规 SPWM的比较研究[J].电力电子技术,1999,2(1)∶25-28.
[8]侯利民,李洪珠,王巍.空间电压脉宽调制 SVPWM的原理及DSP的实现[J].辽宁工程技术大学学报,2007,26(6)∶898-900.
[9]CHUANG D W.Unified voltage modulation technique for real time three-phase power conversation[J].IEEE Trans on IA,1998,34(2)∶374-380.
[10]求是科技.MATLAB 7.0从入门到精通[M].北京∶人民邮电出版社,2006.
[11]孙屹.Simulink通信仿真开发手册[M].北京∶国防工业出版社,2004.

