基于熵值法的组合模型用电量预测方法研究
卓元志,刘家军,王明军,张小庆,刘益瑾
(1.西安铁路局安康供电段,陕西安康725200;2.西安理工大学水利水电学院电力系,陕西西安710048;3.陕西电力科学研究院,陕西西安710054)
电力系统的中长期负荷预测是配电网规划的基础,对实现电网的安全经济运行起着重要作用。地区的年用电量受该地区的经济、气候、人口等多方面因素的影响,不同的影响因素之间有时还存在着严重的相关性[1],因此,对地区的年用电量进行中长期负荷预测时,要选用能够将这些影响因素考虑进去的负荷预测模型,那么其年用电量预测结果才能正确的反映该地区的年用电量情况。在对地区的年用电量进行中长期负荷预测时,组合预测方法是一种有效的方法,该方法首先采用不同的单项预测方法从不同的角度反映地区的年用电量情况,其次根据某种准则对各个单项预测方法赋予一定的权系数,最后得出年用电量的组合预测结果,因为组合预测模型考虑了多种因素对电力负荷的影响,因此,得到的结果一般要优于单一模型预测方法的结果[2-3]。
本文在建立年用电量组合预测模型时,各个单项模型分别按照年度、季度、月度和行业用电量发展的不同规律,分别采用对应适当的方法进行求解[4],依次得出年度、季度、月度和行业用电量预测值,然后将每年的4个季度用电量预测值相加得到该年用电量的一种预测值;再将每年的12个月用电量预测值相加得到该年用电量另一种预测值;再将该预测年的第一、第二、第三产业年预测值相加得到该年国民经济全行业用电量预测值再与该年城乡居民用电量预测值相加得到该年用电量第4种预测值,然后将上述4种单一方法的年用电量预测结果进行线性组合,同时采用熵值法[5]求解组合预测模型的权系数,最后得出该年用电量预测值。算例证明了该组合模型综合利用了各种方法所提供的信息,克服了单一方法的缺陷,提高了预测精度。
1 组合预测模型的建立
在进行用电量负荷预测时,从年用电量、季度用电量、月用电量和行业用电量的不同角度分析,可以发现用电量负荷发展的不同规律。对于年度用电量发展序列,可以根据负荷的变化趋势采用趋势分析法进行拟合预测。用电量在一年里的不同季节,不同季度和不同月份呈现出比较稳定的统计特性,此即用电量的季节特性[6]。我国属于季节性气候,每年的四季季节性比较明显,地区的年用电量受该地区气候影响很大,因此,地区的年用电量也具有较强的季节性特点。一般说来,夏季和冬季是用电量较大的季节,春季和秋季的用电量则相对夏季和冬季较少一些。因此,对于季度用电量发展序列,可以根据用电量的季节特性采用虚拟变量法或季节调整的X12方法等具有周期性特点的方法进行负荷预测;用电量不仅有季节特性,同时月度用电量也有其周期性的特点,一般说来,月度用电量高峰在每年夏季的7、8月份,同时冬季的12月份也可能接近夏季的7、8月份月度用电量;1、2月份是全年月度用电量的峰谷,3—7月是全年月度用电量的持续增长时期,但是有可能会出现反复现象,9—11月比夏季的7、8月份月度用电量有所下降,但是其用电量趋势比较稳定。所以根据月度用电量的季节特性同样可以采取虚拟变量法或季节调整的X12方法等具有周期性特点的方法进行负荷预测。对于行业用电量的负荷预测,可以采用部门分析法或者虚拟变量法和季节调整的X12方法等具有周期性特点的方法进行各行业用电量预测。
本算例中,因为年度用电量具有线性增长趋势,可采用趋势分析法进行计算并得到年用电量预测值.因为季度、月度和行业用电量同时具有季节周期性,因此,采用季节调整的X12方法、虚拟变量法分别进行计算并得到季度、月度和行业用电量预测值,接着依次将该年4个季度用电量预测值相加得到该年用电量预测值,然后采用基于误差平方和最小的组合模型对其权系数进行求解,最后得出该年用电量预测值;依次将该年12个月用电量预测值相加得到该年用电量预测值,然后采用基于误差平方和最小的组合模型对其权系数进行求解,最后得出该年用电量预测值;依次将该年4个行业用电量预测值相加得到该年用电量预测值,然后采用基于误差平方和最小的组合模型对其权系数进行求解,最后得出该年用电量预测值.
在依次得出4种年用电量预测值后,将上述4种单一方法的年用电量预测结果进行线性组合,同时采用熵值法求解组合模型的权系数,最后得出组合模型年用电量预测值。该模型分别从年度、季度、月度和行业4个方面对年用电量进行分析,较充分考虑了地区的年用电量特点,同时也较好地反映了年用电量发展的实际情况。
2 基于熵值法权系数的确定
2.1 建模优点
年用电量预测受大量不确定性因素的影响,如何在预测模型中综合考虑各种误差的影响,对预测的准确性至关重要。基于熵值法的年用电量预测方法综合考虑了各影响因素,对不同的影响因素赋不同的权值,可以有效提高预测的精度[7-8],也有效克服了加权组合评价法中根据单一误差赋权值的缺陷[9]。
2.2 基本思路
由于年用电量预测受大量不确定性因素的影响,影响负荷预测变化的因素很多,而单一方法只能反映某一信息或某几种信息,不能完全反映负荷发展实际情况。熵值法根据不同的预测方法提供不同的预测信息和预测精度,将不同的预测方法进行加权组合,以综合利用各种方法所提供的有用信息,从而可提高模型的预测精度。这就是熵值法的基本思路[10-11]。
2.3 组合模型的建立步骤及求解
在信息论中,熵是对不确定性的一种度量。信息量越大,不确定性就越小,熵也就越小;信息量越小,不确定性越大,熵也越大。根据熵的特性,我们可以通过计算熵值来判断一个事件的随机性及无序程度,也可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响越大。

首先定义组合模型的预测相对误差:令则称eit为第i种预测方法第t时刻的预测相对误差,i=1,2,…,m,t=1,2,…,N。显然,0≤eit≤1,(eit,t=1,2,…,N)。为第i种预测方法在各个t时刻的预测相对误差序列,i=1,2,…,m。
设年用电量的负荷数据序列为{xt,t=1,2,…,N},组合预测模型中共有m种单项预测方法,其中第i种预测方法第t时刻的预测值记为xit,i=1,2,…,m,t=1,2,…,N。同时设l1,l2,…,lm为组合模型的权系数。它满足归一性和非负性,即具体建模步骤为[12]:
1)将组合模型中各单项预测方法的相对误差进行归一化,即计算第i种单项预测方法在第t时刻的预测相对误差比重

显然

2)计算第i种单项预测方法的熵值hi

其中,k>0为常数,hi≥0,i=1,2,…,m
对第i种单项预测方法而言,如果Pit全部相等,即Pit=1/N,t=1,2,…,N,那么hi取极大值,即

所以取

则有:0≤hi≤1。
3)计算第i种单项预测方法的差异系数di
因为0≤hi≤1,根据系统某项指标的熵值的大小与其变异程度相反的原则,所以定义第i种单项预测方法的预测相对误差序列的差异系数di为:
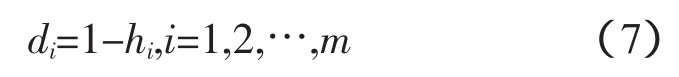
4)计算各单项预测方法的权系数l1,l2,…,lm
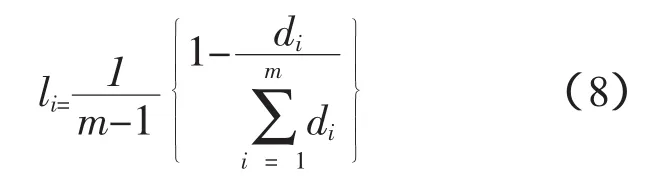
上式体现了一个原则:某个单项预测方法预测误差序列的差异程度越大,则其在组合预测中对应的权系数就越小。显然权系数满足

5)计算组合预测值
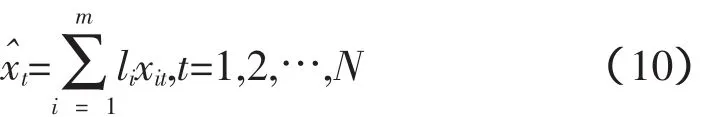
3 算法实例
3.1 单一预测模型预测
根据某省电业局统计,采用4种单项预测方法进行了预测,2004—2009年各年年用电量情况及各单项预测方法的预测值如表1所示。
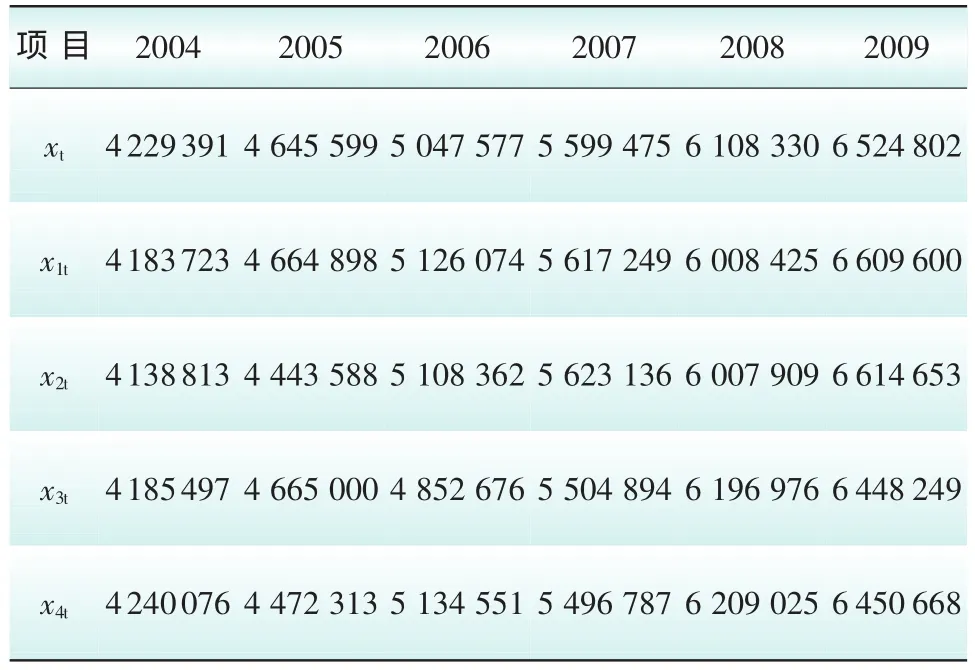
表1 实际值和4种单项预测方法预测值 万kW·h
表1中xt表示各年年用电量实际值,x1t,x2t,x3t,x4t分别表示按照年度、季度、月度、行业用电量发展序列进行预测得出的预测值,表2同此表示。
3.2 组合预测模型的建立和求解
由上述可知,采用4种单项预测方法对2004—2009年某省年用电量数据进行了预测,然后对4种预测模型的相对误差序列进行归一化处理,并计算4种单项预测模型的预测相对误差的熵值h1、h2、h3和h4为:h1=0.922505,h2=0.887246,h3=0.887157,h4=0.893070,再计算4种单项预测模型的预测相对误差序列的差异系数d1、d2、d3,d4为:d1=0.077495,d2=0.112754,d3=0.112843,d4=0.106930,最后计算出4种单项预测模型在组合预测模型中的权系数l1,l2,l3,l4为 :l1=0.270332,l2=0.241668,l3=0.241596,l4=0.246403,从而可以建立组合预测模型为:

表2 预测效果评价指标体系
如果采用常用的基于误差平方和最小为准则的组合预测模型,可得如下最优化模型:

利用matlab最优化工具箱计算出相应的组合预测权重系数为l1=0.088449,l2=0.3356805,l3={0.4410179},l4=0.1348529。
3.3 2004—2009年年用电量预测效果分析
为了验证本文基于熵值法的组合预测模型的有效性,选择以下5个误差指标评价预测效果:
1)平方和误差

2)均方误差
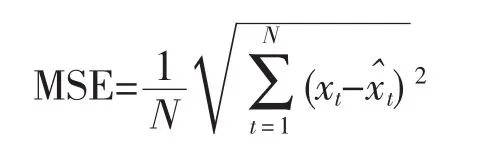
3)平均绝对误差

4)平均绝对百分比误差

5)均方百分比误差

由本节分析可知,基于熵值法的组合预测模型预测效果评价的5个误差指标的计算结果如表2所示,从表2来看,各个单项预测方法的评价指标值均明显高于的评价指标值,而且与相比在预测精度上也有一定程度的提高。
4 结语
本文采用基于熵值法的组合预测方法在对年度用电量进行预测时,尽管单个预测方法的选择不一定具有最好的代表性,但基于熵值法的组合预测方法可以充分利用各个单项预测方法的信息,从而较全面地反映了负荷发展的实际情况,而且该方法与传统的基于误差平方和最小定权系数的方法相比,预测精度也得到了一定的提高,实例证明该方法是有效的。
[1] 杨宗麟,顾宇桂,温权.华东地区电力与经济发展关系研究[J].华东电力,2007(4):41-43.
[2] 刘昊,张艳,高鑫,等.基于RBF神经网络与模糊控制的短期负荷预测[J].电网与清洁能源,2009,25(10):62-66.
[3] 张建华,邱威,刘念,等.正交设计灰色模型在年电力负荷预测中的应用[J].电网与清洁能源,2010,26(2):28-32.
[4] 刘家军,王明军,姚李孝,等.基于Theil不等系数的IOWHA算子组合模型年用电量预测新方法[J].现代电力,2010,27(5):44-48.
[5] 王琦,王花兰.基于熵值法的城市汽车保有量组合预测[J].交通科技与经济,2009(6):53-55.
[6] 吴疆.我国用电量季节特性研究以及在电力运行走势分析中的应用[J].中国电力发展与改革研究,2009(12):33-38.
[7] 朱成骐,孙宏斌,张伯明.基于最大信息熵原理的短期负荷预测综合模型[J].中国电机工程学报,2005(19):1-6.
[8] 李春生,王耀南.基于条件熵的电力负荷组合预测模型[J].电力系统及其自动化学报,2007(4):55-58.
[9] 王德金.基于熵权法的电力中长期负荷组合预测[D].北京:华北电力大学,2007.
[10] 苏恒强,陈桂芬,朱春娆.基于熵值法的玉米产量组合预测模型[J].沈阳农业大学学报,2010(1):125-127.
[11] 张庆宝,程浩忠,刘青山.基于最大熵原理的中长期负荷预测综合模型的研究[J].继电器,2006(3):24-27.
[12] 陈华友.熵值法及其在确定组合预测权系数中的应用[J].安徽大学学报:自然科学版,2003,27(4):1-6.

