高层框筒结构剪力墙抗侧移及最优厚度分析

□文/黄雅娜

高层框筒结构剪力墙抗侧移及最优厚度分析

□文/黄雅娜

文章以正交异性板宏单元法理论及其对应Fortran程序为依据，验证Sap2000有限元软件对框筒结构进行受力及侧移分析的有效性。在此基础上对四筒高层建筑结构中不同厚度及不同位置的剪力墙板抗侧移能力进行对比，分析其在满足侧移要求前提下，获得最大经济效益的剪力墙厚度。

高层框筒；剪力墙；抗侧移；最优厚度

在高层结构设计中，侧向风荷载和水平地震作用所产生的结构内力与位移是结构设计的控制因素。随着建筑物高度的增加，对结构抗侧刚度的要求也随之提高。

1 框筒结构介绍

与一般框架结构相比，密柱深梁的框筒结构是一种立体结构，在水平力作用下，翼缘框架与腹板框架共同工作，提高了整个结构的抗推刚度，使结构侧移减小很多。但是立体结构的有效性取决于结构剪力滞后效应的大小。在一个完全的立体结构中，水平力作用下所引起的弯曲应力达到理想的分布状态，即翼缘墙上的轴力，近似呈均匀分布，腹板墙上的轴力，近似呈三角形线性分布，见图1a。而一般有四片框架组成的框筒结构在水平荷载作用下发生整体弯曲所引起的轴力，不论是翼缘框架还是腹板框架，均呈曲线分布，如图1b，降低了立体结构的有效性，减小了结构的抗推刚度，水平荷载下的结构侧移也就随之增大。

图1 侧力作用下的立体结构的应力分析

高层建筑中的外框筒，有时因设计者希望提供一个较好的视野，要求外圈框架的柱距适当加大，裙梁较矮。然而这种稀疏框架筒体在风或地震等水平力作用下，因剪力滞后效应显著而不能有效发挥立体结构的空间作用，产生较大的顶点侧移和层间位移，难于满足规范要求以及使用者的风振舒适感。为解决这一问题，设想将框筒中的填充墙换成或部分换成厚度适中的抗剪墙板，来增大结构的抗推刚度，减小结构侧移。

2 剪力墙抗侧移分析

2.1 理论背景

高层束筒建筑板块法理论采用力法体系给出了多筒高层框筒结构的宏单元法。这是一种半解析法，兼有数值法与精确法的优点，使用比较方便，便于进行快速计算机辅助设计与优化。本方法将整个筒体结构分为平板（框架板或实腹剪力墙板）与角柱2种单元，外荷载作用在角柱上，平板为平面应力问题，当平板为框架板时按正交异性板计算，当为实腹墙板时按各向同性板计算。把平板与角柱连接处的分布内力作为未知量，平板采用正交异性板二维弹性理论级数解，角柱作为悬臂梁单元处理，然后用板梁形变协调条件，求出结线上内力分布，这样就可得到各板任一点的内力与应力分布。

2.2 框筒轴力分析

计算一个20层、层高3m的高层框筒并分为单筒和四筒2种情况分析，荷载及截面见图2。采用高层束筒建筑板块法理论编制相应的Fortran程序及有限元软件Sap2000分别计算，计算结果比较见表1和表2。

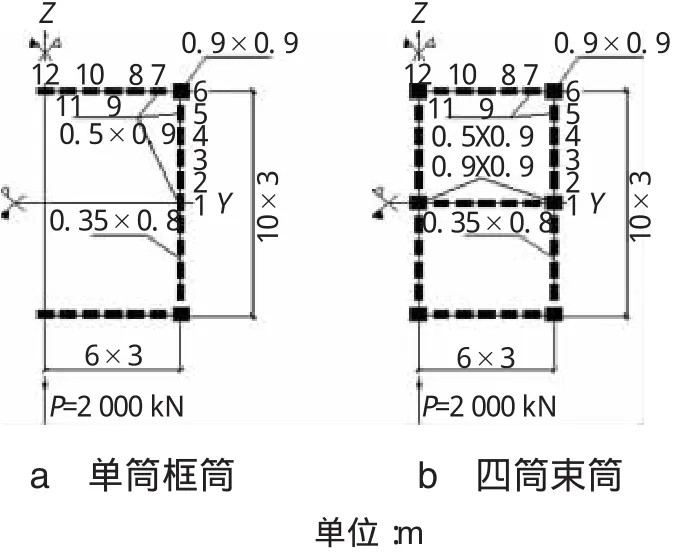
图2 框筒算例

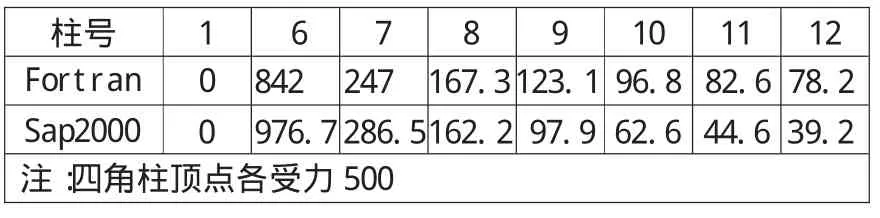
表1 单筒基底柱轴力 kN

表2 四筒基底柱轴力 kN

由表1和表2可以看出，Sap2000结果与Fortran程序理论解析解基本吻合。

2.3 剪力墙抗侧移分析

将高层框筒结构中的填充墙换成侧向刚度很大的剪力墙板，计算在不同位置布置不同厚度剪力墙板的顶点位移。

根据底部剪力法估算多遇地震时的水平地震作用为沿Z向分别布置作用在外围6根脊柱上的倒三角荷载，共1200kN/m(八度)、600kN/m(七度)。八度地震作用下，分为3组布置剪力墙，第1组只在受力方向布置1片剪力墙，即将中间沿Z向的1榀框架中的填充墙改为剪力墙板，见图3；第2组，在受力方向布置3片剪力墙，即将中间沿Z向的3榀框架中的填充墙改为剪力墙板，见图4；第3组，在受力方向交错布置3片半榀剪力墙，见图5。各顶点水平侧移见图6-图8。七度地震作用下，分为两组布置剪力墙，第4组，只在受力方向布置1片剪力墙，与第1组相同；第5组，在受力方向分散布置6短片剪力墙，见图9。各顶点水平侧移见表6。

图3 第1组剪力墙板布置

图4 第2组剪力墙板布置

图5 第3组剪力墙板布置

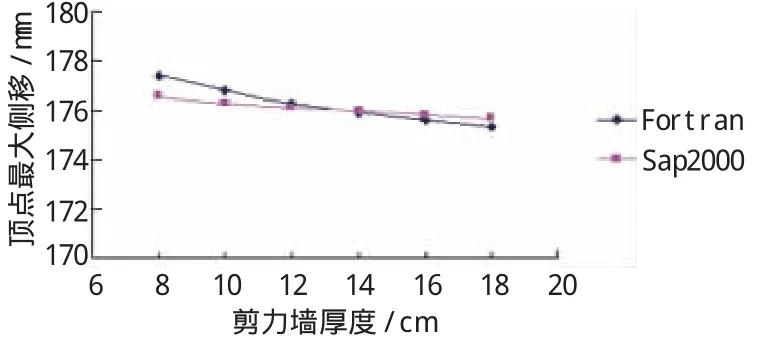
图6 第1组不同墙厚的顶点侧移

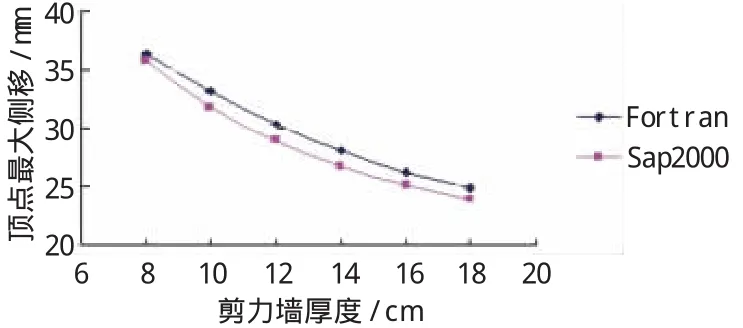
图7 第2组不同墙厚的顶点侧移

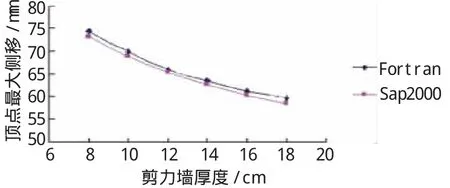
图8 第3组不同墙厚的顶点侧移

图9 第5组

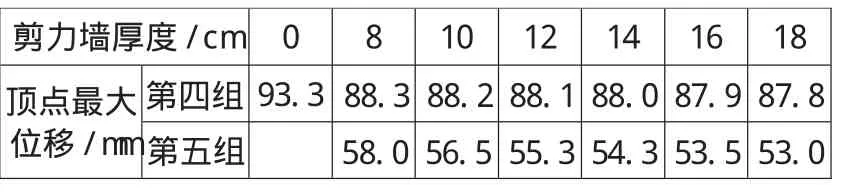
表6 第4～5组剪力墙板顶点侧移

软件Sap2000与Fortran程序算出的结果相符合，能够较好地分析框筒的受力及位移。相同厚度的剪力墙数量与顶点最大位移成反比，但并非线性。第1组，剪力墙集中布置在中跨，角柱与中柱顶点位移相差很大且角柱为位移控制点，即使增加墙体厚度也无法有效控制顶点侧移，剪力墙布置不合理。第2组，剪力墙数量相对第1组增大了3倍，侧向顶点位移＜H/800（规范顶点侧移控制）且由于门窗开洞要求，无法布满剪力墙，故此组剪力墙布置不合理。第3组，剪力墙数量相对第1组增大了0.5倍，顶点位移减小了60%～70%。同理，七度区抗震，由于地震作用减小，剪力墙无需布置太多。第5组剪力墙数量比第4组增加了20%，顶点侧移减小了34%～40%，可以较好地控制侧向顶点位移，满足规范要求。第3组和第5组的剪力墙布置合理，顶点侧移均以角柱的顶点侧移来控制。可见，合理布置剪力墙的位置可以有效控制顶点位移。

将部分填充墙改设为剪力墙并合理控制剪力墙数量和布置剪力墙位置，结构的抗侧刚度有很大提高，在地震作用下的侧向位移有明显减小。由多组数据可以得出，剪力墙板的厚度在8～14cm之间，厚度的增加对结构侧向位移的减小比较明显。

3 剪力墙最优厚度分析

选取合理剪力墙布置 (第3组和第5组)，应用SAP2000分析结构分别在八度及七度地震荷载作用且设定顶点侧移刚好约为H/800=75mm的前提下，进行结构经济性分析。随着剪力墙厚度的变化，结构梁柱尺寸也在变化，从而导致钢筋混凝土用量及使用面积的变化，造价及获利值的变化，从而找到最大获利增量对应的剪力墙厚度范围。见表3和表4。

设原框筒内外填充墙为200mm厚的空心砖，钢筋混凝土造价500元/m3，空心砖造价125元/m3，房屋销售价格5000元/m2。

表3 第3组剪力墙设置八度区抗震

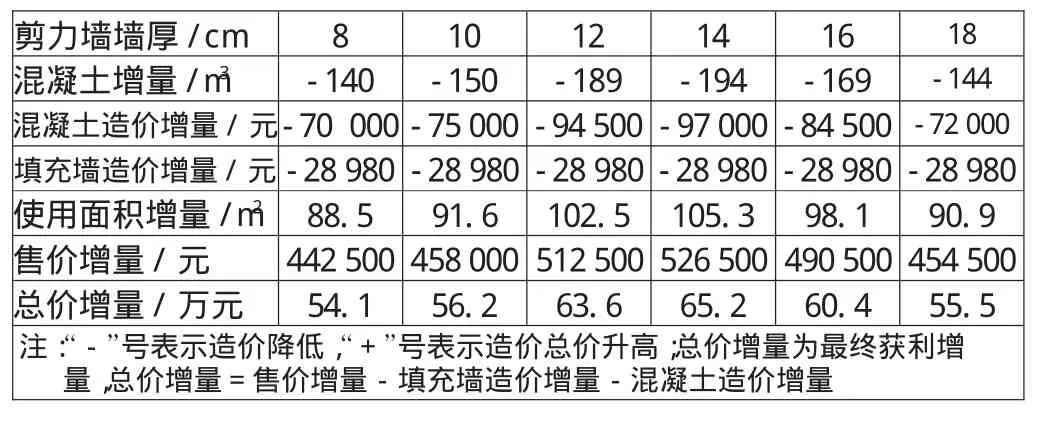
表4 第5组剪力墙设置七度区抗震

由表3和表4看出，在顶点位移控制下，相同剪力墙数量及布置结构，通过协调剪力墙厚度及钢筋混凝土梁柱尺寸，可有效减少钢筋混凝土用量，增加使用面积，从而获得最优的经济效益。而此时最大经济效益对应的剪力墙厚度为最优厚度解，即当剪力墙厚取约14cm厚时，可获得最大的经济利益。

4 结论

本文是在高层束筒建筑板块法理论的基础上，提出了一种新的结构形式薄剪力墙抗侧力结构并对其在稀疏框筒中的应用进行了初步的探索。这种结构形式是将原结构中的部分填充墙改为较薄的剪力墙 (厚度＜16cm），增加了结构的抗侧刚度，减小了梁柱截面，在几乎不增加结构造价的基础上可以提高结构的整体性和抗震性能。

[1]王修信.高层束筒建筑板块法理论[J].宁波大学学报，1994，7（2）：57-66.

[2]李爱群，高振世.工程结构抗震与防灾[M].南京：东南大学出版社，2003.

[3]包世华.高层建筑结构设计和计算[M].北京：高等教育出版社，2004.

[4]齐永顺，杨玉红.自密实混凝土的研究现状分析及展望[J].混凝土，2007，(1):25-28.

[5]沈蒲生，孟焕陵.框筒结构梁柱截面基于剪力滞最小的合理高度[J].建筑科学与工程学报，2005，22（3）：16-19.

TU398.2

C

1008-3197（2011）01-19-03

2010-12-09

黄雅娜/女，1983年出生，助理工程师，硕士，天津城投建设有限公司，从事土建技术管理工作。