集群下Cholesky分解的核外预取算法

刘 凤,刘青昆

(辽宁师范大学 计算机与信息技术学院，辽宁 大连 116081)

随着科学技术的迅猛发展，人们需要处理的数据量迅速增长。大规模并行应用涉及的数据量是非常惊人的，内存容量常常不能满足涉及到大数据量计算问题的存储需求。因待处理数据无法全部读入内存，所以只能保存数据到外部磁盘系统。当程序运行时，某个时刻只能将部分数据调入内存并参加计算，并且在适当的时候写回外存，通过某种策略实现内外存数据的交换。由于运算过程中数据并没有全部存放在内核存储器中，所以称之为核外计算。核外计算程序中包含大量的文件操作，因访问磁盘数据的速度比较慢，所以在处理大数据量问题时，I/O性能显然要超过CPU性能而成为重要的限制因素。因此，如何对核外数组进行合理调度与高效访问是解决核外计算应用问题的关键。

利用三角分解式求解对称正定方程组是一种有效方法。单行卷帘存储Cholesky分解[1]使每个节点所分配的数据最多相差一行，但是这种划分方式的通信开销比较大。多行卷帘存储Cholesky分解[2]可以减少通信开销,充分利用节点的缓存，但是没有充分考虑缓存的效率问题，因为缓存可以对程序性能带来巨大的改变。递归算法[3]通过将矩阵分块使各个子矩阵的运算能够在高速缓存中进行，以提高运算效率，同时递归算法良好的数据局部性和矩阵递归的分块，使其非常适合分层多级存储的计算机结构。但是在递归调度算法中，非对角块的运算不能充分利用计算机的分级存储结构。分块Cholesky分解[4-5]通过精心的挑选块的大小，使每个块都能充分地利用一级缓存，并且合理地划分块的大小还能使每个块常驻内存。参考文献文[4]充分利用了系统硬件的并行机制以使通信与计算重叠，减少了节点的等待时间。同时通过矩阵元素的重排使每个块都被连续存储，以充分利用计算机的多层次存储结构，减少数据拷贝和内部的变化。但是这些算法只在数据量较小的情况下适用；当数据量较大时，数据将无法一次性读入内存，因此引进了核外计算的概念。

本文对Cholesky分解的并行算法进行了深入的研究，给出的核外算法通过预取[6-7]的方法使得数据在实际使用之前从硬盘移到缓存中,从而进一步提高了缓存的命中率，减少了文件读取的时间。

1 基本概念

1.1 Cholesky分解

Cholesky分解用于求解系数矩阵对称正定的线性方程组。

式(1)中，A为实对称正定矩阵，且A的所有顺序主子式均不为零，X和b为矩形矩阵或向量。为了避免平方根法Cholesky分解 (A＝LLT)的开方运算且扩大使用范围，将矩阵对称正定矩阵A分解成A＝LDLT。当A是正定对称矩阵时，A的分解是唯一的。其中D是对角线元素全为正的对角矩阵，L是单位下三角矩阵。其求解公式如下：

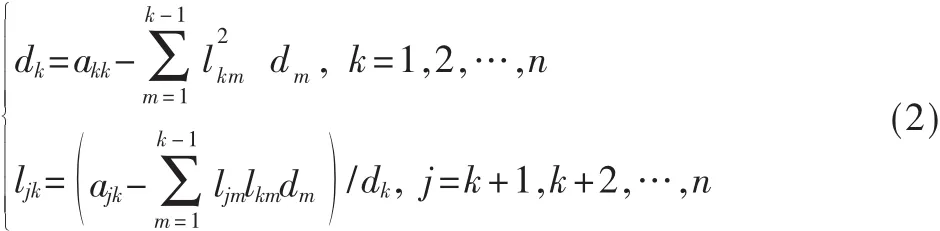
1.2 预取方法

在核外计算中数据存储在磁盘上，只有CPU对数据进行处理时才将其读入内存缓冲区，处理完成后写回文件。这样，核外计算过程就可以描述成：读入核外数组文件的一块数据到内存缓冲区，进行计算等处理，处理完成后将其写回数组文件；读取下一块数据，进行数据处理，处理完成后写回文件。如此反复执行，直到整个核外数组处理完成后结束。显而易见，这是一个顺序流水线，执行I/O操作与CPU进行计算是顺序执行的；由于二者在执行前需彼此等待，所以程序的执行效率非常低。于是考虑到，当I/O操作的数据与CPU执行计算的数据无相关性时，可以把对下一个数据块的I/O操作与对当前数据块的计算重叠起来，这样就可以隐藏I/O的延迟，达到缩短整个程序运行时间的目的。图1所示为数据预取前后的对比。

本算法采用双缓冲区的方式，即为一个核外数组分配两个内存缓冲区buffer[2]，轮流存放本次和下一次读入的数据块。用预取的方法对第s个子文件更新，其伪码如下：

图1 数据预取前后的对比

(1)主节点将第一个子文件读入内存数组buffer[0]中，并将其广播出去；

(2)依次用已分解的子文件更新第s个子文件，即对ka=1,2,……,s-1循环：

若该节点是主节点,做以下工作：①读入第ka个文件到buffer[ka%2]中；②发送第ka个文件;

若该节点是从节点,则做以下工作：①用第ka-1个文件更新第s个文件；②接收第ka个文件。

(3)若该节点是从节点，则用第s-1个文件更新第s个文件。

2 用预取算法实现Cholesky分解

2.1 Cholesky分解并行算法的思想

将大规模矩阵A连续拆分成q个子文件，并将其储存到主节点中。主节点一次调入内存一个子文件，依次对各子文件进行Cholesky分解，直至最后一个子文件分解完毕。所以只要拆分的子文件大小不超过空闲内存的范围，算法就可以运行。其算法流程见图2，具体步骤如下：

(1)文件拆分过程

由主节点机进行矩阵拆分存储的操作，打开存储于硬盘中的A.txt文件，依内存容量的需要进行拆分，读取相应规模的数据，生成子文件，并将这些子文件j.txt(j=1,2,3)存储回硬盘。

(2)A阵的Cholesky分解过程

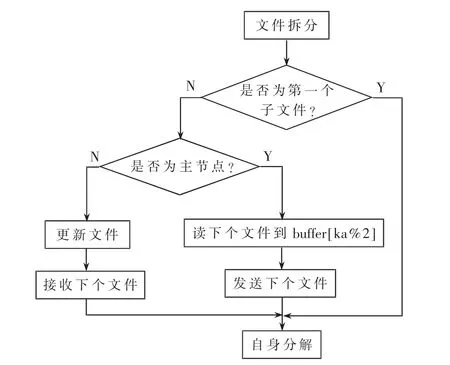
图2 Cholesky分解流程图

考虑到Cholesky分解过程中的依赖关系，对其由上至下依次进行分解。由于在三角分解中，既需要分解后的上三角，又需要分解后的下三角，所以可以将分解后的上三角复制到下三角。这样既可以减少运算量又可以减少存储量。在分解过程中利用其并行性，主节点打开第一个子文件 1.txt后，赋值给 a6×15，再将 a广播出到各个从节点。每个从节点经卷帘计算出分解因子后，广播出去，如此地计算kb=2次，该子文件的Cholesky分解完毕。当1.txt计算结束后,主节点打开下一个子文件2.txt，赋值给a6×15，再将 a广播到各个从节点。同时主节点还要打开分解完毕的子文件 1.txt,赋值给 aa6×15(即 buffer[0]),再将aa广播到各个从节点。各个从节点用aa6×15卷帘去更新 a6×15，更新完毕后 a6×15再像上面的操作，每个从节点卷帘的计算出分解因子后，广播出去，如此的计算kb=2次后，主节点打开下一个子文件3.txt，进行如文件2.tx的操作。

2.2 Cholesky分解并行算法的描述

将A连续拆分存储到q个子文件中，依次对各子文件进行Cholesky分解，直至对最后一个子文件分解后，原大规模系数矩阵已被拆分到几个小文件中存储。将节点机分别标记为 P0，P1…Pnp，np代表从节点机个数，P0代表主节点，kb表示在一个子文件中单个节点机计算的行数，s是子文件依次分解的循环控制变量，ka表示读取已分解子文件的循环控制变量，在拆分后 a∈R[kb×np]×n，aa∈R[kb×np]×n。 具 体 步 骤 如 下 ：

(1)文件拆分

主节点机打开存于硬盘中的A.txt文件，按内存容量的需要进行拆分，读取相应规模的数据，生成q个子文件。

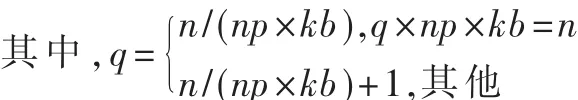
(2)A矩阵的Cholesky分解过程

①1.txt(s=0)的 Cholesky分解：(a)主节点打开 1.txt，读取文件内容，赋值到a[np*kb][n]数组中，并将数组a广播出去。(b)从节点 myid(myid=1,2,……,np)将数组 a中的第 i行(i%np=myid-1)进行 Cholesky分解。(c)从节点将已分解的对角元素赋给数组d[n]。(d)从节点用数组a已分解的元素重写其下三角。(e)从节点将分解后的数组a写回主节点。

②文件 j.txt(s=1,2,……,q-1,j=s+1)的 Cholesky分解：(a)主节点打开并读取 j.txt内容，赋值到a且将其广播出去。(b)用预取的方法对第j个子文件更新。即主节点依次打开已分解文件 ka.txt(ka=0,1,…,s-1)，赋值给buffer[ka%2]，并将 buffer[ka%2]广播出去。在各个从节点根据buffer[ka%2]的值更新数组a值的同时，主节点读取下一个已分解的文件。(c)用数组buffer[ka%2]的元素重写数组a的下三角。(d)将数组a进行Cholesky分解。(e）将数组a本次分解的对角线元素赋值给数组d[n]。(f)用数组a本次分解的元素重写其下三角。(g)将分解后的数组a写回主节点。

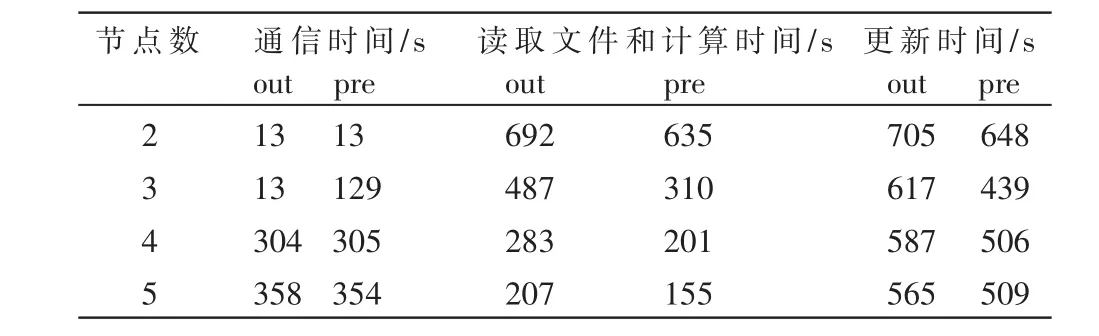
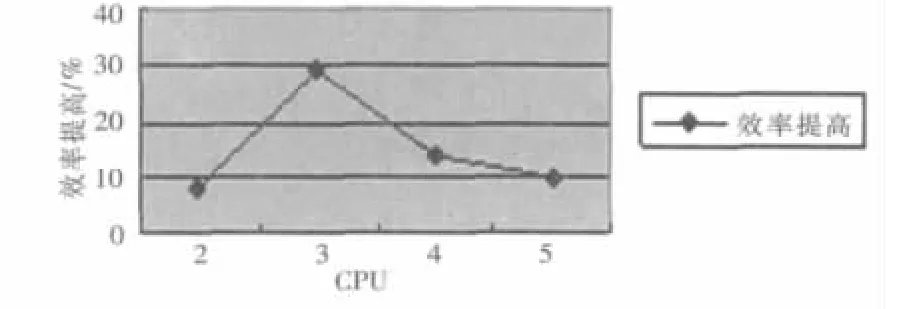
2.3 算法的复杂度分析

对于点对点的通信，测量开销使用乒乓法：节点0发送m个字节给节点1；节点1从节点0接收m个字节后，立即将消息发回节点0。总的时间除以2，即可得到点到点通信时间，也就是执行单一发送或接收操作的时间。通信开销的解析表达式是消息长度m(字节)的线性函数：tcomm(m)=Ts+Tb×m;其中 Ts表示通信的启动时间,Tb表示发送每个字节所需时间 (它是带宽的倒数)。由于MPI_Bcast函数采用树算法，所以一次MPI_Bcast的通信开销为 tcomm(s)×logP。Cholesky分解的执行时间可分为子文件的更新时间和自身分解时间。因此，Cholesky分解时间：Tc=Tg+Tf，其中 Tg是子文件更新时间，Tf是自身的分解时间。在文件的更新时间中,又细化为读文件时间Td、计算时间Tj和通信时间Tt。为了减少分解的执行时间，本文通过预取的方法使更新过程中的读文件与计算重叠，使得 Cholesky分解的时间开销：Tc

子文件的大小是通过参数kb(1≤kb≤n/np)而设定的，当kb=n/np时相当于无文件划分并行求解；当kb=1时，在每个子文件中每个节点机只计算一行，此时的通信量最大(按照这种分配方法划分数据后，每个处理器上须存储的内容为kb×np×n规模的矩阵 A)。因此算法的并行执行时间：Tn=T1+Tc+T2，其中，T1为划分子文件消耗的时间，Tc是Cholesky分解时间，T2为冗余的控制和管理开销。

3 实验测试与结果分析

实验环境采用由5台主频为2.8 GHz的Intel Xeon CPU，内存为ECC DDR-2 SDRAM 2 GB的Dell PowerEdge 2850构建的集群。该集群运行Linux RH9操作系统，并且建立了MPI并行编程环境。本文测试的两个程序分别为：带状循环划分的核外程序out和带状循环划分的核外预取程序pre。

表1表示当A的阶数n=2 478,核外Cholesky分解各个部分的执行时间对比。表2表示了在节点数np分别为2,3,4,5时，Cholesky分解中的子文件更新各个部分的时间对比(kb=10,n=2 479)。图3为核外预取程序相对于核外程序更新时间的效率提高百分比。

表1 矩阵规模n=2 478,Cholesky分解各部分执行时间

由表1可见，在求解过程中Cholesky分解中的更新部分占了大部分时间，所以提高更新部分的执行率能明显缩短总的执行时间。

表2 out和pre的Cholesky分解更新时间对比

图3 pre相对于out的更新时间效率提高百分比

由表2可见，预取方法使得子文件的更新时间平均缩短了15%左右。

图3表明，核外预取分解并行算法的效率明显好于核外分解并行算法，并且随着节点个数的增加，提高的效率先增大后减小。这是因为随着节点数目的增加，子文件容量增加，计算量增加，计算与文件读取的重叠时间越多。在节点数np=3时，效率提高幅度最大。当节点数np>3时，随着节点数的增加通信时间急剧增加，而计算时间逐渐减少，计算与文件读取的重叠时间减少，所以执行效率提高的幅度降低。

本文通过对Cholesky分解并行算法的研究，表明预取方法是计算核外稠密线性方程组的有效方法，非常有利于缩短I/O与CPU速度间的差距。数据预取的方法可以做到计算与I/O并行，即在计算一块数据的同时读入下一块要处理的数据。为了存放预取的数据，本文采用双缓冲区的方式，即为一个核外数组分配两个内存缓冲区，轮流存放本次和下一次读入的数据块。此外，预取方法同样适用于QR分解、LU分解、高斯削去等其他线性代数问题。当然采用数据预取技术时，I/O操作时间与CPU执行时间的比例是保证预取效果的关键。

事实上，Cholesky分解也可以采用数据重用的方法。通过减少对子文件的读取次数，可以进一步提高Cholesky分解算法的效率。由于目前分布存储计算机的处理速度都很高，而其网络通信速度较慢,所以用增加计算和通信粒度的办法来降低通信成本。

[1]迟学斌.Transputer上Cholesky分解的并行实现[J].计算数学，1993(3):289-294.

[2]王顺绪，周树荃.卷帘行存储下的一种并行Cholesky分解及其在PAR95上的实现[J].南京航空航天大学学报，1999，31(4)：428-432.

[3]陈建平.Jerzy Wasniewski，Cholesky分解递归算法与改进[J].计算机研究与发展，2001，38(8):923-926.

[4]GUSTAVSON F G,KARLSSON L,KAGSTRO B M.Distributed SBP cholesky factorization algorithms with nearoptimal scheduling[J].ACM Transactions on Mathematical Software,2009,36(2):1-25.

[5]ANDERSEN B S,GUNNELS J A,GUSTAVSON F G,et al.A fully portable high performance minimal storage hybrid format cholesky algorithm[J].ACM Transactions on Mathematical Software,2005,31(2):201-227.

[6]丁文魁，汪剑平，向华，等.p-HPF并行编译系统核外计算的实现及优化策略[J].计算机学报，1999，22(10):1042-1049.

[7]姚维.Linux下一种磁盘节能的预取算法[J].计算机系统应用，2010,19(7):91-94.