中国单沟泥石流危险度评价模型比较研究

张怀珍，范建容 ，郭芬芬，刘 飞

(1.中国科学院 水利部 成都山地灾害与环境研究所，成都 610041;2.中国科学院研究生院，北京100049)

泥石流是山区常见的一种自然灾害现象。由于泥石流形成过程复杂，暴发突然，来势凶猛，历时短暂，破坏力极大;严重危害山区人民的生命财产安全，制约社会经济的发展。我国山地和高原面积约占国土总面积的66%;大部分山区具备泥石流形成的基本条件，加之人类活动的影响，是我国成为世界上泥石流灾害最严重的国家之一。据近年统计资料:我国泥石流的活动区域面积约为430万km2，其中活动强烈的地区达130万km2;有8万处泥流活动，其中严重的有8 500处[1]。对泥石流进行研究，对泥石流的活动规模、危害程度等进行评价预测;对减轻泥石流灾害造成的间接和直接损害，保障人民生命财产安全具有重要的意义。

国际上，日本学者可能是最早涉及到泥石流危险度评价[2-3]，在1977年提出了泥石流发生危险度这一概念。在1981年美国学者Hollingsworth和Kovacs提出了基于打分方法的泥石流危险度评价框架，基本思路是先将岩性、坡度和切割密度3个因子分别划分为5个等级，再用因子叠加求和进行危险度评价。这可能是美国最初的，也是为数不多的涉及到的泥石流危险度的定量评价。我国学者谭炳炎是较早开始泥石流沟严重程度的数量化综合评判和危险度研究的学者[4]。近年来，广大科研工作者对泥石流危险性评价的研究不断深入，将灰色系统理论、模糊数学理论和GIS技术等引入到泥石流危险性评价中，使得泥石流危险性评价的研究得到了长足的发展，研究成果的实用性和可操作性不断加强。

1 单沟泥石流危险度评价模型

刘希林曾将我国泥石流危险度评价研究发展分为4个阶段时期:(1)90年前的最早的单沟泥石流危险度评价;(2)20世纪90年代初期的单沟泥石流危险度评价;(3)20世纪90年代中期的单沟泥石流危险度评价;(4)20世纪90年代后期及以后的最新单沟泥石流危险度评价[4]。本文根据这些模型的赋值方法特点，将其分为3种类型:分级评分模型，分级赋值模型和函数赋值模型。

1.1 分级评分模型

分级评分模型主要是20世纪90年代前的单沟泥石流危险度评价模型。这种模型出现的最早，影响较大，其基本原理和技术方法得到了广泛的应用和认可。基本原理是:首先根据实地情况选取泥石流危险度评价因子，依据一定的原理方法和测度(如关联度)确定各危险度评价因子的权重和权数，再根据一定分级评分方法确定单沟泥石流危险度查找表，然后计算各危险因子在危险度查找表中的评分总和，即为单沟泥石流危险度，其危险度W 计算公式可表达为:

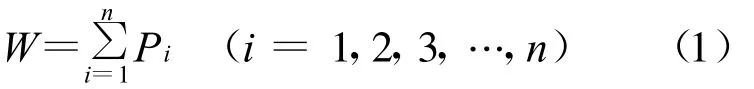
式中:Pi——第i个评价因子在危险度查找表中的评分;n——评价因子总个数。

1.2 分级赋值模型

分级赋值模型主要是20世纪90年代的单沟泥石流危险度评价模型，此时分级赋值的赋值结果是在0～1之间的小数。此类模型可以划分为两个阶段:(1)90年代初期的单沟泥石流危险度评价;(2)90年代中期的单沟泥石流危险度评价。

90年代初期的单沟泥石流危险度评价模型和分级评分模型类似。这个时期的模型已经将危险度评价因子划分为主要因子和次要因子;在各因子分级赋值时不再是因子评分，而是其参数大小在其评价因子中的影响比重。在危险度计算中，突出主要因子的权重和权数。其危险度Rd计算公式为:

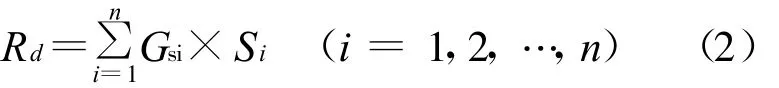
式中:Gsi——第i个评价因子所占的权重;Si——第i个评价因子在泥石流沟等级评分查算表中的定量赋值;n——选取的评价因子总个数。计算得到的危险度其值介于0～1。其值的大小能够表示暴发泥石流的可能性大小，即可以理解为发生泥石流的概率大小。

90年代中期的单沟泥石流危险度评价模型是对90年代初期模型的改进。最主要的是减少又重复影响的次要评价因子;选取与主要因子关联度较大的次要因子;增强主要因子的主导地位。另外，这一时期的评价模型还增加了评价因子的划分等级，提高了评价因子取值变化对危险度评价结果的灵敏度。其危险度计算公式与90年代早期的模型类似。

这种90年代出现的分级概率类模型其基本原理和技术方法基本已经成型，在四川、云南、北京和贵州等地得到了推广应用[2]。刘希林、唐川等在这方面的研究做出了重大贡献。

1.3 函数赋值模型

函数赋值模型在90年代末期出现，此类模型是由我国学者刘希林提出，属于最新的单沟泥石流危险度评价模型[5-7]。这类型的最大改进和完善就是危险因子赋值完全脱离危险度分级查找表，各评价因子采用不同的转换函数(见表5)采用公式化赋值。转换函数公式化赋值有效避免了采取分级赋值时的赋值结果的间断跳跃性。其危险Hd计算公式为:

式中:M ，F ，S1，S2，S3，S5，S7分别为 L1，L1、S1，S2，的转换函数赋值(泥石流规模 L1、泥石流发生频率L2、沟谷流域面积 S1、主沟长度 S2、流域相对高差、流域切割密度S5和不稳定沟床比例S7)。

这一类型的危险度评价因子仍分别选定主要因子和次要因子，但这类模型选定的次要因子个数进一步减少;选定的次要因子不但关联度要与主要因子较大，而且这些次要因子的确定性要更加明确。

2 单沟泥石流危险度评价应用实例

在泥石流危险度评价研究中不断引入了多种理论和技术，如灰色系统理论、模糊数学理论、GIS技术、多元回归分析和神经网络等。其中灰色系统理论和模糊数学理论较为成熟并得到广泛推广，GIS技术在泥石流危险度研究中的应用会得到不断推广。

本文主要运用基于灰色系统理论的关联度分析方法，对云南省37条典型泥石流沟进行危险度评价。所用基础数据主要参考1994年朱静发表的论文“泥石流沟判别与危险度研究”[8]和由刘希林、唐川编著1995年出版的《泥石流危险性评价》[9]。

2.1 分级评分模型危险度评价

我国学者朱静在1994年以云南泥石流形成环境的区域调查为基础，收集整理了云南省40条典型泥石流沟的11项因素参数[3](表1，40条中的37条)，分别为:流域面积S1(km2)，主沟长度 S2(km)，流域相对高差S3(km)，主沟平均比降S4，流域切割密度S5(km2/km)，松散固体物质储量 S6(万m3)，泥砂补给段长度比S7，植被覆盖率S8(%)，主沟弯曲系数S9，形成区山坡平均坡度S10(°)和24 h最大降雨量S11(mm);同时也考虑了泥石流最大一次冲出量L1(万m3)和泥石流暴发频率L2(次/100 a)。

表1 云南省37条典型泥石流沟基础数据[8]

其危险度评价的主要思路是首先把收集到的资料按4级分级由轻微-严重分别赋予1，2，3，4分值确定各因素与危险度之间的关联性量度，以确定各因素的关联序，用来计算各因素在判别泥石流危险度时的权重。采用的是古德曼(Goodman)和卡拉斯卡尔(Kruskal)的r度量来确定关联性指标与危险度之间的关联性大小，r的计算公式如下:

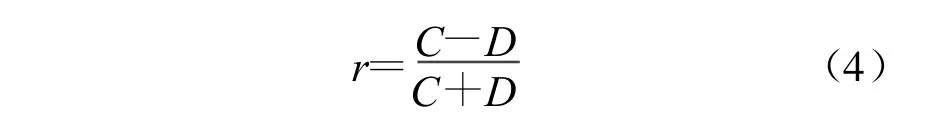
式中:C——某因素与一次最大冲出量的样本对在其有序尺度变量X和Y上协调时的数目;D——某因素与一次最大冲出量的样本对在其有序尺度变量X和Y上不协调时的数目[3];nij，nkl——在四级分级取值中，某因素与一次最大冲出量的样本对在其有序尺度变量X和Y上协调时取1;不协调取0。

经计算得出各因素的关联序为:

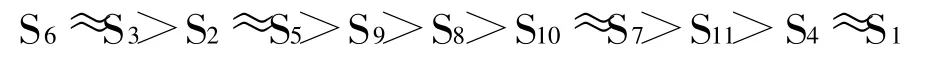
从关联度最小的因素S1开始，给定起始权数为1，以此基本单位为公差，依次以等级数向关联度变大的方向递增权重，得到个因素的权重;经计算可得S1-S11的权重以次为:0.022 2，0.133 3，0.155 6，0.222 2，0.133 3 ，0.155 6 ，0.066 7，0.088 9 ，0.111 1 ，0.066 7 ，0.044 4。由此计算出泥石流危险评价各因子评分表(表2)。

最后根据式(1)计算各条泥石流沟的危险度，其计算结果见表6。

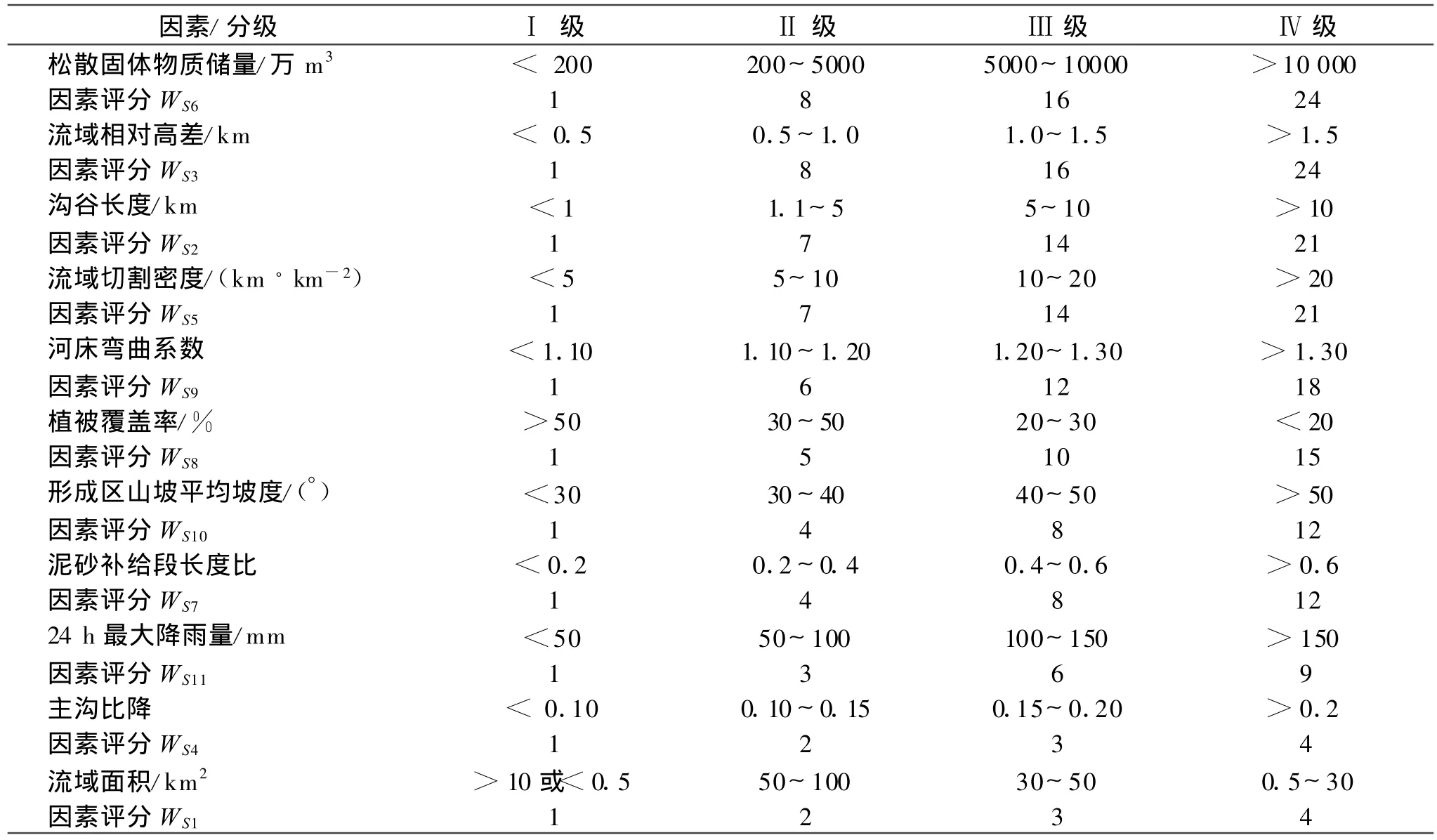
表2 泥石流危险评级因子分级、评分

2.2 分级赋值模型危险度评价

刘希林、唐川在1995年同样以云南省37条典型泥石流沟为研究对象[9]，收集整理了16项评价因子，其中包括2项主要因素和14项次要因子;主要危险因子为一次泥石流(可能)最大冲出量L1和泥石流发生频率L2;次要危险因子为流域面积S1，主沟长度S2，流域最大相对高差S3，主沟平均比降 S4，形成区山坡平均坡度S10，流域切割密度S5，主沟床弯曲系数S9、松散固体物质储量S6，泥砂补给段长度比S7，24 h最大降雨量S11，年平均降雨量S12，植被覆盖率S8，垦殖指数S13和流域内人口密度S14。其中L1、L2与S14见表3，其他参考表1。

通过对全国范围内劲100位泥石流专家学者的通信调查，采用邓聚龙教授创立的“灰色系统理论”中的灰色统计方法，成功解决了泥石流主要危险因子确定的关键问题。根据灰色统计方法，设定关联度阈值(L10.85;L20.83)最终选取确定主要危险因子为一次L1和 L2;次要危险因子为 S1、S2、S3、S5、S9、S7、S11和S14。使用灰色关联分析法，根据关联度特性和各危险因子的平均关联度确定各危险因子的权数和权重[9]。

所谓灰色关联分析就是先用均值化方法把原始数据做无量纲化处理，求出均值化矩阵;再计算主导因子序列与各关联因子序列相互比较的差值的绝对值;找出最大绝对差值和最小绝对差值;用公式(5)计算出关联系数ξij;再按公式(6)计算主导因子与关联因子间的关联度R。

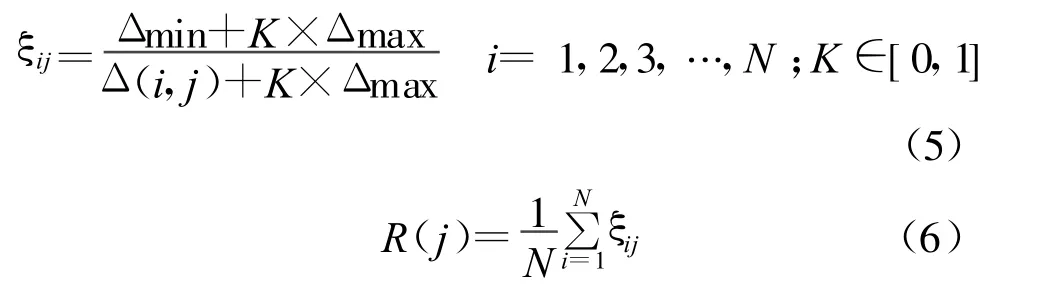
式中:R(j)——主导因子与其他各因子间的关联度;N ——样本数;i——第i个样本;j——第 j个关联因子;Δ(i，j)——主导因子与关联因子比较后的绝对值;Δmax——所有差值序列中的最大绝对差值;Δmin——所有差值序列中的最小绝对差值;K——经验系数，只影响关联系数的大小，不影响关联序列。

表3 云南省37条典型泥石流沟基础数据[9]

经计算可得，L1和 L2的权数为16，其权重为0.235 3;S1，S2，S3，S5，S9 ，S7，S11，S14的权数依次为8，6，5 ，7，1，4，3 ，2;其权重系数依次为 0.117 6，0.088 2，0.073 5 ，0.102 9 ，0.014 7 ，0.058 8 ，0.044 1，0.029 4 。各危险因子的取值范围较大，制定出统一的危险因子等级和危险度标准，采用对称不等分间隔分割法来划分泥石流危险因子的等级并赋予定值(表4)。最后得到危险度计算公式(7)，计算各泥石流沟的危险度Rd，计算中所用 L1、L2与S14参考表3，其计算结果见表6。

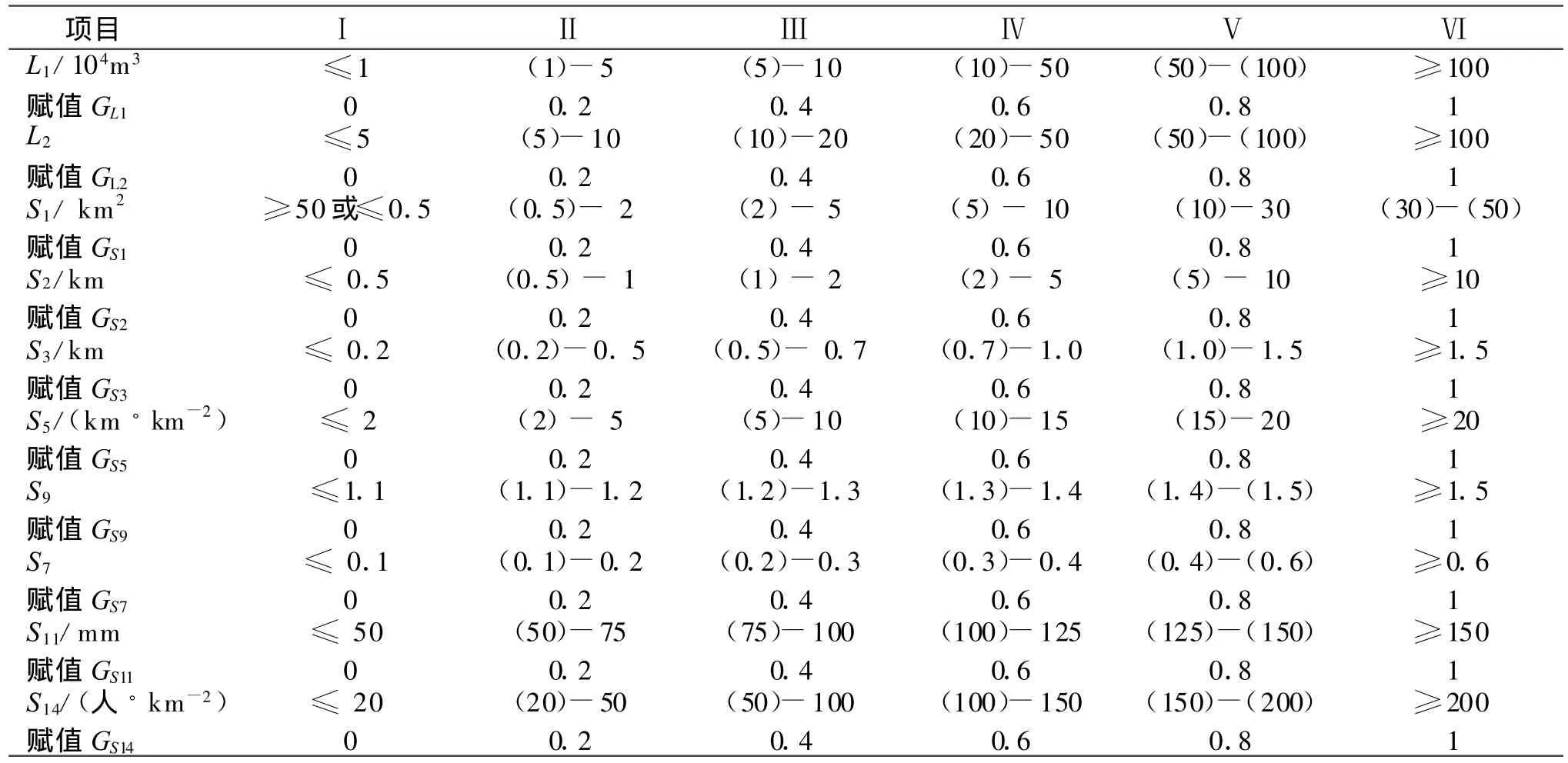
表4 泥石流危险因子等级及其赋值(1994年修订)

2.3 函数赋值模型危险度评价

刘希林进一步改进模型，他首先将14个候选次要因子分别与泥石流规模和发生频率进行关联度分析，再根据每个候选次要因子与泥石流规模和发生频率得出的2个关联度的平均值，确定其与主要因子关系的密切程度并决定其取舍，即双系列关联度分析方法。最后选取单沟泥石流危险度评价的7个因子:泥石流规模L1、泥石流发生频率L2、沟谷流域面积S1、主沟长度S2、流域相对高差S3、流域切割密度 S5和不稳定沟床比例S7，并提出了最新沟谷泥石流危险度Hd计算公式(3)[5-6]。依此计算云南省37条典型泥石流沟的危险度 Hd(表6)。其中计算过程中所用L1与L2参考表3。

3 评估模型比较分析

3.1 模型比较

分级评分模型的不足之处主要是难以获取的泥石流内在因子较多，降低了评价方法的可操作性，未能突出发生频率的主要因子地位。但朱静根据实际情况，以云南泥石流形成环境的区域调查为基础，选取确定了泥石流沟危险度判定的11项因子，采用的是古德曼(Goodman)和卡拉斯卡尔(Kruskal)的r度量来确定关联性指标与危险度之间的关联性大小。经过实际应用，该方法具有较高的可靠性和实用性[2]。

分级赋值模型选取多项因子用来评价泥石流沟的危险度，开始采用标准化量值，在标准化方面有了较大进步，得到了较广的应用。刘希林、唐川等在90年代中期对模型进行了改进，选取了10项因子，去除具有重复意义的因子，在各因子权重分配时突出主要因子的权重。其对模型的改进主要是将评价因子等级的4级划分改为6级划分，提高了评价因子取值变化的灵敏度;调整了大部分评价因子取值的上下限，使其更符合实际情况;明确了各等级间的取值界限，避免了评价因子取值界限模糊而导致的危险度取值的可变性。由于因子减少，准确度提高，获得了较为广泛的认同和引用，在我国四川、云南、北京、贵州和辽宁等地推广应用[2]。

函数赋值模型是对分级赋值模型做的进一步改进，泥石流危险度评价因子减少至7个;因子的确定性更加明确。采用函数公式计算评价因子的转换值，使评价因子的转换值连续变化于0～1之间，避免了评价因子分级结合点出现转换值的跳跃式变化[2，5]。

3.2 基础数据比较

对云南省同样的37条泥石流沟的基础数据进行对比，朱静和刘希林、唐川获取的部分(危险度评价)因子参考数据存在差异，主要是泥石流发生频率、松散固体物质储量和植被覆盖率。部分泥石流沟在其他评价因子参数方面也存在差异，其中一次泥石流(可能)最大冲出量存在较大差异的有东川因民沟和巧家白泥沟。存在较多差异的评价因子参数有着不同的计算方法，这些方法有间接性的，也有直接性的;不确定性较大。例如，一次泥石流(可能)最大冲出量L1的间接计算公式[1]之一:

计算泥石流发生频率L2的间接计算公式[1]为:

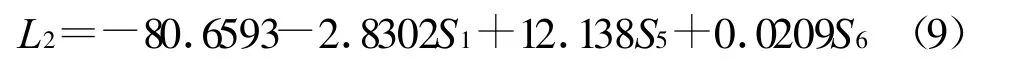
3.3 危险度评价结果比较

泥石流危险度是遭受到泥石流危害的可能性大小;故泥石流沟危险度是一个概率[9]。分级赋值模型和函数赋值模型的泥石流危险度的计算过程正是基于概率，其值0～1之间，可以理解为发生泥石流的可能性大小。分级评分模型基于泥石流沟危险因子等级评分表，得分越高，遭遇泥石流危害的可能性越大。理论上，如果各危险因子都是最高评分，即得到最高评分，那么它的危险度应该为1。将其转换为概率度量，其转化公式为:

3种模型对云南省37条典型泥石流沟危险度进行评价的结果如表6所示。为更直观观察3种模型的评价结果，绘制了3种结果的统计图(图1)。对3类模型危险度评价结果作相关性分析，3种模型危险度评价结果之间的Pearson correlation(皮尔逊相关系数)极高;其中Wd与Rd之间的相关系数为0.919;Wd与Hd之间的相关系数为0.941，Hd与Rd之间的相关系数为0.958。研究结果表明，3种模型的危险度评价结果具有较高的相似程度。朱静曾对模型危险度评价结果进行验证，选取40条泥石流沟，其吻合率达80%，其余20%的判定值高于实际值一个量级，其验证结果表明其模型具有较好的可靠性。

图1 3种模型危险度结果对比图

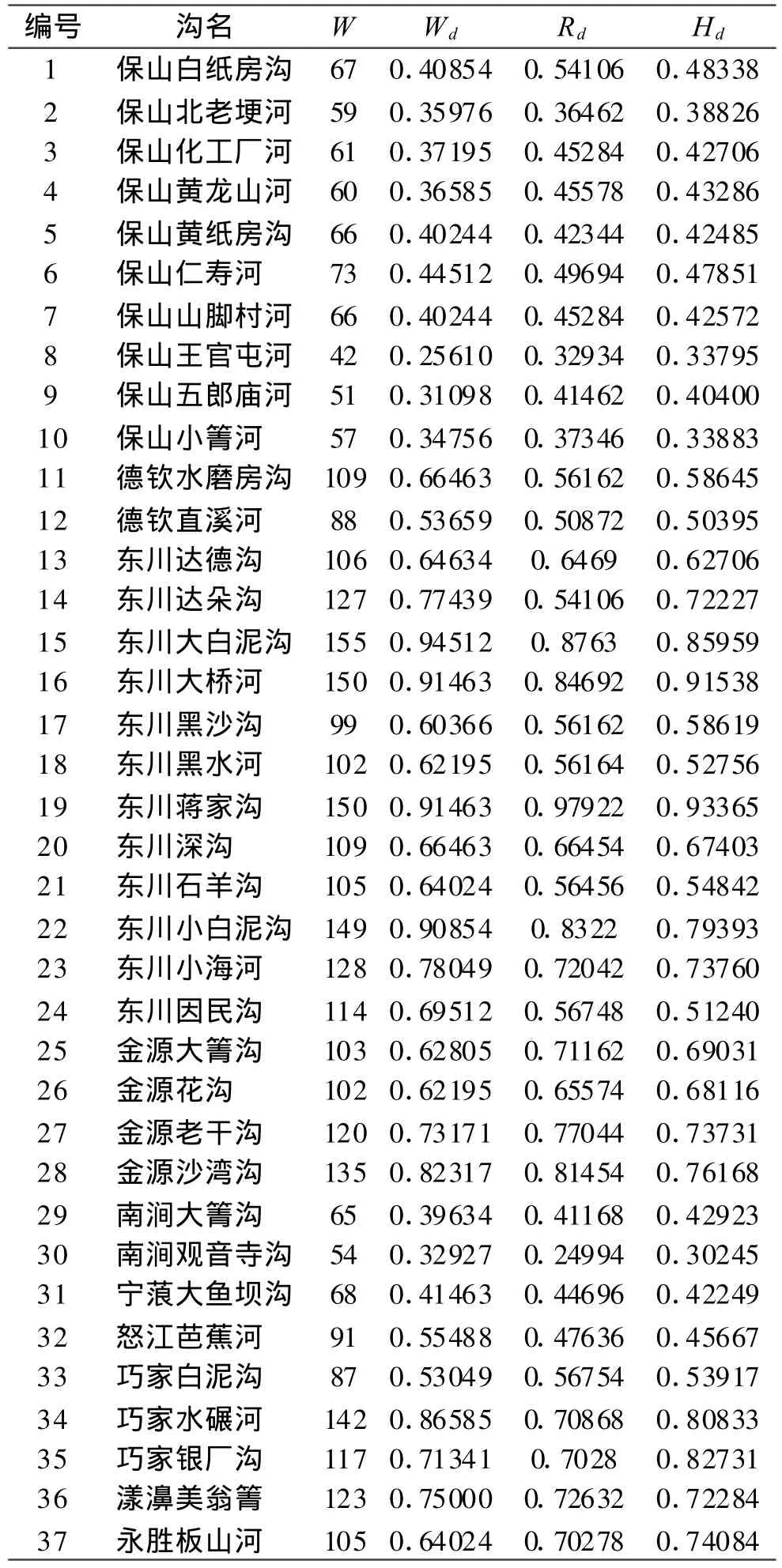
表6 云南省37条典型泥石流沟危险度评价结果

3类模型危险度评价因子参数存在不确定性，但其结果差相似程度极高，笔者认为主要原因是在泥石流沟危险度评价时，朱静选用了11种评价因子，其中松散固体物质储量S6和植被覆盖率S8所占权重只有0.155 6，0.088 9，减少了不确定性产生的误差;刘希林和唐川运用分级赋值类模型时只选取了泥石流发生频率，并突出了主要因子的权重，不确定性产生的误差也减小;函数赋值模型也只选取了泥石流发生频率，且选用了确定性较强的因子，有效减小了不确定性因子的影响。

分级赋值模型和函数赋值模型通过计算关联度，选取影响较大的评价因子。但泥石流是一个复杂的过程，其影响因子较多，不同环境下的泥石流，各影响因子的作用各异。如云南省37条典型泥石流沟的14项危险因子与一次泥石流(可能)最大冲出量L1和泥石流发生频率L2的平均关联度均大于0.824 2。

4 结语与展望

泥石流的产生和形成是一个十分复杂的过程，其影响因素较多且复杂。运用不同的方法选取主要因子和增加主要因子的权重是可行的;通过对3类模型的运用实例和结果分析，表明次要因子同样对泥石流危险度评价有影响，多种次要因子共同的作用对危险度的评价具有较大的影响[10-11]。如朱静选择11项评价因子(次要因子)的评价结果与刘希林等选择主要因子并突出主要因子权重的评价结果有较高的相似性，即:次要因子的影响不可完全忽视。

近年来，科研人员对泥石流研究的不断深入，多种科学理论的不断引入。泥石流沟危险度评价已经有定性化发展成定量化评价;并且评价因子的赋值也公式化，避免了跳跃性。模型的实用性和准确性会不断提高[12]。笔者认为，单沟泥石流沟的危险度评价具有时间性。泥石流多发于雨季，一定时间内的降雨量是泥石流暴发的激发因素。同一地区雨季与非雨季的泥石流危险度不同，一般情况下，非雨季时泥石流暴发的机率极小;当部分危险因子发生巨变时可能激发泥石流。笔者认为泥石流危险度评价可以为:

式中:∑GiPj——主要影响因子计算得到危险度;τ(t)——随时间变化较大的评价因子(如降雨量)计算得到危险度;φ(t)——突发事件产生的巨变影响(如地震);μ——修正系数。具体的评价模型需要进一步的研究确定。

现在，遥感技术已经迅猛发展，遥感定量化有了较大进步，可靠性不断增强。通过遥感影像定量提取泥石流危险度评估因子参数的可操作性、直观性会不断增强。如，一次最大冲出物，松散固体物储量及泥石流发生频率等。今后，遥感技术能够为泥石流灾害防治和灾害实时监测等提供更加有效准确的科学数据依据。

[1] 康志成，李焯芬，马霭乃，等.中国泥石流研究[M].北京:科学出版社，2004:5-16.

[2] 刘希林.我国泥石流危险度评价研究:回顾与展望[J].自然灾害学报，2002，11(4):1-8.

[3] 刘希林.泥石流危险度判定的研究[J].灾害学，1988，3(3):10-151.

[4] 谭炳炎.泥石流沟严重程度的数量化综合判别[J].水土保持通报，1986，6(1):51-57.

[5] 刘希林.沟谷泥石流危险度计算公式的由来及其应用实例[J].防灾减灾工程学报，2010，30(3):241-245.

[6] Liu X L.Assessment on the severity of debris flows in mountainous creeks of southwest China.Proceedings of International Symposium of Interprevention[C]∥Garmish-Partenkirenchen，Germany，1996:145-154.

[7] LIU Xilin，ZHANG Dan.Comparison of Two Empirical Models for Gully-Specific Debris Flow Hazard Assessment inXiaojiang Valley of Southwestern China[J].Natural Hazards，2004 ，31:157-175.

[8] 朱静.泥石流沟判别与危险度研究[J].干旱区地理，1995，18(3):63-71.

[9] 刘希林，唐川.泥石流危险性评价[M].北京:科学出版社，1995:1-26.

[10] 李泳.泥石流危险性评价的问题[J].山地学报，1999，17(4):305-312.

[11] 刘希林.泥石流风险评估中若干问题的探讨[J].山地学报，2000，18(4):341-345.

[12] 侯兰功，崔鹏.单沟泥石流灾害危险性评价研究[J].水土保持研究，2004，11(2):125-128.