大功率机车轮轨接触应力计算分析

周新建,卢 勇,王成国,肖 乾,,张 怀

(1 华东交通大学 载运工具与装备教育部重点实验室,江西南昌330013;2 中国铁道科学研究院 铁道科学技术研究发展中心,北京100081;3 中国科学院 研究生院 计算地球动力学实验室,北京100049)

目前国产大功率机车已批量下线并投入运用,促进了我国民族工业发展,形成了以重点企业为核心、配套企业为骨干、辐射上百家相关企业的国内机辆装备设计制造体系。大功率机车走行部,尤其是车轮这类关键零部件。实现国产化的最重要步骤就是需要对目前大功率机车的现场运行情况有非常清晰地了解,掌握全面的基础数据。轮轨接触应力分析是轮轨接触问题的基础。对于机车车轮来说,必须明确其在不同工况下与钢轨的接触特性,因此,完成大功率机车的轮轨接触应力计算分析就迫在眉睫。

1 轮轨接触的有限元计算模型

1.1 轮轨接触的非线性理论

接触问题通常采用增量方法求解,与一般的非线性问题区别在于每一个增量步中都必须将接触的约束条件作为定解条件和校核条件判断接触状态。也就是说,计算时,首先得到和时间t+Δt位形内平衡条件相等效的虚位移方程,然后在此基础上求得其T.L.或U.L.格式方程,一般式描述如下:

式中M是节点质量矩阵,K为节点刚度矩阵,P为节点载荷矩阵,μ为节点位移,M取零值为静态接触问题。这里需要特别指出的是根据拉格朗日乘子法和罚函数法引入约束条件的不一样,接触问题有限元求解方程的具体形式也有区别。对于这些非线性有限元方程组,可以采用显式解法或隐式解法进行求解。显式解法求解接触问题时,通常采用二步形式的中心差分法进行递推[1],即有:

而隐式解法常常采取Newton-Raphson方法进行迭代求解,N-R的迭代公式为[2]:

显式解法不仅可以避免每一增量步的迭代步骤,而且可以避免摩擦滑动接触状态时非对称刚度矩阵的求逆运算,但在每个时间步长内没有误差检查和迭代步骤,计算误差不能控制。而隐式解法的优缺点与显式求解正好相反,能保证求解精度但计算时间相对较长。为了保证良好的计算精度,轮轨接触有限元计算采用隐式求解法。隐式算法的计算速度主要由计算机内存决定,采用并行计算能完成单机无法计算的大规模有限元模型,考虑到计算模型规模比较大,用单机无法胜任,所以采用有限元并行计算。

1.2 轮轨接触的计算模型

1.2.1 轮对有限元模型

大功率机车车轮几何模型是以HXD2机车车轮参数绘制,直径为1 250 mm,采用磨耗型(JM)踏面。由于网格细化是保证计算精度的主要手段之一[3],文献[4]以对有限元两次分析的结果进行比较,如果二者相差小于2%,说明当前的网格密度和单元类型足以保证工程分析精度,指出在轮轨计算中,单元尺寸须小于等于0.75 mm。为了有较好的精度,对车轮可能接触的区域进行局部网格细化,细化区网格尺寸为0.5 mm,采用一阶六面体减缩积分单元(C3D8R)进行离散,整个轮对产生733 995个单元和758 126个节点。

1.2.2 钢轨有限元模型

钢轨采用的是75 kg/m国内标准轨,纵向长度取5 m。根据轮对细化相同的原理,对钢轨可能的接触区域进行网格细化,细化区最小单元尺寸为0.5 mm。钢轨也采用一阶六面体减缩积分单元(C3D8R)进行离散,两段钢轨共产生252 030个单元、267 430个节点。

1.2.3 模型的材料、边界条件以及接触面的定义

轮轨材料模型为经典的双线性弹塑性本构模型,材料本构曲线如图1。轨距为1 435 mm,轨底坡为1:40,轴重Q为25 250 kg,重力加速度为9.81 m/s2,泊松比υ为0.3。根据UIC 510-5[5]标准规定的计算载荷,对应直线运行时的受力状态。车轮受到垂直方向力的作用:

式中Q是单个车轮承受的质量,g为重力加速度。通过公式(4)可求得单个轴箱上所要承受的载荷为154 814 N。加载时以集中应力形式加载在轮对两端轴箱位置处,同时约束钢轨底面的所有自由度。接触面定义为柔性体间的面面接触,接触算法选用扩展的拉格朗日算法,摩擦模型选用罚摩擦模型。轮轨接触有限元模型见图2。由于轮轨接触有限元模型规模较大,采用中国科学院研究生院计算地球动力学实验室的网络集群并行计算环境,该并行系统计算节点的配置为2颗4核E5520处理器、8G DDR3内存和146GSAS接口的HP Proliant BL280c G6刀片服务器,根据ABAQUS6.9.1并行求解器的特点,采用12个节点共96核进行接触有限元并行计算。

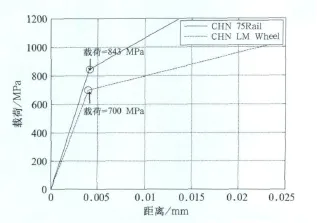
图1 轮轨非线性本构曲线

图2 轮轨接触有限元网格图

2 轮轨接触应力的计算分析

在不考虑超高和冲角的条件下,对车轮横移量为-9,-6,-3,0,3,6,9 mm 7种工况下的轮轨接触情况进行计算,获得了不同横移情况下的接触斑形状、接触斑面积、车轮的表面最大接触压应力、车轮最大Mises应力以及车轮的最大等效塑性变形量等。

2.1 大功率机车轮轨接触应力的基本计算分析

表1所示的是大功率机车车轮横移为0时的轮轨接触计算结果。

表1 横移为0时轮轨接触计算结果

图3为轮对横移为0 mm时的轮轨接触Mises应力分布云图,车轮最大Mises应力出现在接触表面以上2.5 mm处的车轮踏面内。图4给出了轮轨最大等效塑性变形分布云图,从图3和图4比较可以发现钢轨的Mises应力大于车轮的,但是由于车轮的屈服应力小于钢轨的(如图1所示),所以在车轮踏面出现了较大的塑性变形区,最大塑性变形点出现位置与车轮最大Mises应力出现位置一致,车轮接触表面也有塑性变形,车轮塑性变形区最大纵向长度为16.5 mm,最大横向长度为6.5 mm,最大垂向长度为5.7 mm。从图5可以看到接触斑横向长度向背离轮缘侧延伸,与Hertz理论的椭圆形接触斑有较大差异。

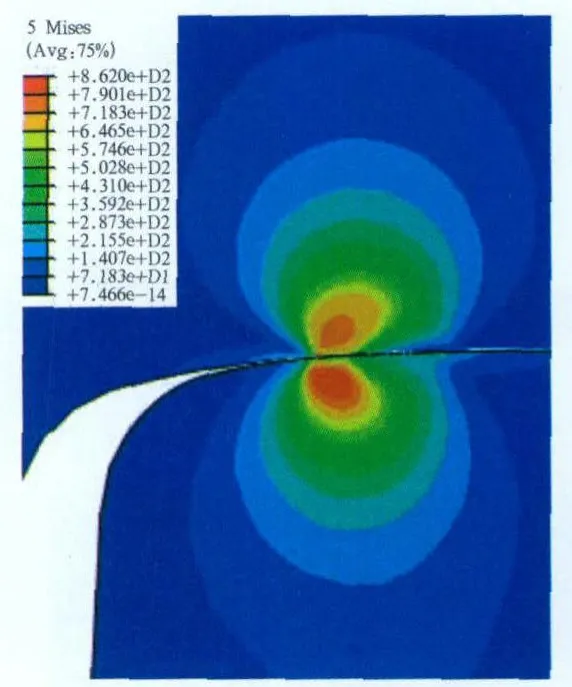
图3 横移为0时轮轨接触的弹塑性Mises应力分布云图

图4 横移为0时等效塑性 变形分布

图5 横移量为0时 接触斑形状

2.2 轮对不同横移对轮轨接触应力的影响分析

参照文献[6],提取不同横移时大功率机车的轮轨接触计算结果(如表2所示)。车轮踏面和轨头都是由多段不同半径的圆弧构成,表 2中所列的 Rwheelprof和Rrailprof分别是指接触斑所处的车轮踏面和钢轨轨头的圆弧半径,从表2中所列的不同横移时的接触斑形状可以看到,轮轨接触具有明显的非Hertz接触特点。

表2 不同横移计算结果数据表

从图6可以看出接触斑横向长度和纵向长度的变化呈现互补特性,即横向长度增大时纵向长度变短,反之亦然。由图6和图7可以看到,在横移量为-3～-6 mm时轮轨接触面积比较大,当横移量绝对值超过6 mm时,轮轨接触面积随横移增大而变小,而且接触面积随横移量的变化曲线与接触斑横向长度随横移量的变化曲线有相同的变化规律。

从图8可以发现,大功率机车轮对横移量的绝对值在6 mm以内变化时,Mises应力变化不大,当横移量从6 mm增加到9 mm时,车轮最大Mises应力迅速升高。这是由于当横移量为9 mm时,车轮踏面接触圆弧最小曲率半径与钢轨轨头接触圆弧最小曲率半径分别为14 mm和15 mm,接触圆弧的变小使得接触压力增大,而且,此时轮轨接触区域为一小半径倾斜曲面,曲面上的点在车轮径向上线速度相差较大,这会导致车轮和钢轨有相对滑动产生,加剧车轮的磨损;接触应力迅速升高也加速了车轮侧磨的发生,所以应减少横移量超过6 mm的时候;最大接触压力随横移量的变化幅度相比最大Mises应力的变化幅度大,横移为6 mm时接触压力最小。

从图9可见,轮对在不同横移时,车轮踏面都发生局部塑性变形。在横移为6 mm时最小,横移量从6 mm变化到9 mm时,最大等效塑性变形量迅速变大。

3 结束语

图6 车轮接触斑长度随横移量的变化

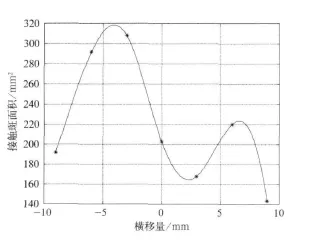
图7 车轮接触斑面积随横移量的变化

图8 车轮踏面体内外接触应力随横移的变化

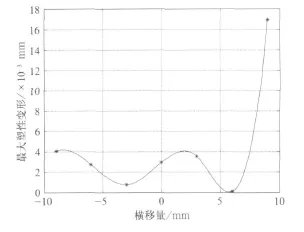
图9 车轮最大塑性变形随横移量的变化

(1)车轮踏面内出现塑性变形,塑性变形从车轮踏面内延伸至接触表面。对横移为0时车轮踏面的分析可知车轮塑性变形区最大纵向长度为16.5 mm,最大横向长度为6.5 mm,最大垂向长度为5.7 mm,而且不同横移时车轮踏面都出现塑性变形,可见车轮踏面塑性变形不可避免。

(2)随着车轮横移量的不同,横向接触斑长度与接触面积有着相同的变化规律,多数情况下的轮轨接触斑形态与Hertz理论的椭圆假设有较大差别。

(3)大功率机车轮对横移量的绝对值在6 mm以内变化时,Mises应力变化不大;当横移量从6 mm增加到9 mm时,车轮最大Mises应力迅速升高,此时车轮和钢轨接触区的最小圆弧曲率半径分别为15 mm和14 mm,小曲率半径圆弧相接触是造成接触应力升高的主要原因。应尽量减少机车横移量超过6 mm的情况。

(4)运用接触有限元并行计算技术可以解决轮轨接触有限元计算的计算规模和计算精度的矛盾,这也是未来用有限元计算轮轨接触状态的趋势。轮轨接触应力应变数据是研究大功率机车车轮的基本依据,计算结果为大功率机车车轮国产化提供理论参考。

[1] TED B,L IU Wingkam,BRIAN M.Nonlinear Finite Element s for Continua and Structures[M].New York:John Wiley&Sons,2000.

[2] 罗喜恒,肖汝诚,项海帆.几何非线性问题求解的改进算法[J].公路交通科技,2005,22(12):75-77.

[3] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2008.

[4] XiaoQian Wang Chenguo GuoGe.”The Research of Parallel Computing for Large-scale Finite Element Model OF Wheel/Rail Rolling Contact”.Proceedings of 2010 3rd IEEE International conference on Computer Science and Information Technology,Chengdu,pp:254-257,July.2010.

[5] UIC 510-5.锻造车轮和轧制车轮[S].国际铁路联盟.2003.

[6] Coenraad Esveld.Modern Railway Track(Second Edition)[M].The Netherlands:MRT-Productions,2001.