一种抗几何攻击的图像水印算法
朱莉莉,门志梅 ,侯迎坤
(1.泰山学院 信息科学技术学院,山东 泰安 271021;2.泰山学院 教务处,山东 泰安 271021)
1 引言
数字水印对几何攻击的鲁棒性在数字水印研究过程中一直是一个热点和难点问题。几何攻击包括旋转、缩放、平移、剪切以及改变长宽比等([1]–[3]).这些攻击都能破坏水印信号的同步,因此它们都能阻止水印信号的正常提取。对此人们想了很多办法也提出了一系列的算法来解决这个问题,现有的有效算法中大多是基于几何不变量的方法来应对该问题,尤其是基于图像归一化技术的算法在近几年成为研究该问题的主流方法。
这类算法的基本思想是从原始图像中找到具有几何不变性的量用来隐藏水印由于具有几何不变性,在水印图像遭受几何攻击后,这些量没有变化。因而隐藏于其中的水印信息得以保存。该类算法的优点是不用确定并恢复几何攻击。
Fourier-Mellin变换是一种具有RST不变性的变换.0’Ruanaidh等[4]首先提出把水印嵌入到Fourier-Mellin变换域中。该算法第一步计算图像DFT(Diserete Fourier transform)。因为图像在空间域内的线性平移只是引起Fourier变换域内的相位线性平移,而幅值不变,因此如果水印嵌入到幅值的子空间里,它对于空间坐标平移具有不变性。第二步,对DFT的幅值进行LPM(Log-Polar Map),这时笛卡儿坐标系变为对数极坐标系。笛卡儿坐标系中的缩放和旋转对应于对数坐标系中的平移。第三步再对对数极坐标上的系数做DFT,只取DFT的幅值,那么得到的空间具有RST不变性。水印嵌入到该空间可以对抗RST.水印图像由两次逆DFT和一次逆LPM得到。事实上,该算法仅仅是理论上的,文献[4]中提到的困难限制了它的应用;而且在512x512x8bit图像上嵌入的信息量也只有13个字符。值得说明的是,该算法实际上是第一个专门设计抵抗几何攻击的算法。上述算法有两个主要缺点:(l)使用这种策略的水印只能抵抗RST,不能同时抵抗剪切、长宽比(Aspect ratio)改变和RST联合攻击中常伴随的剪切等其它攻击;(2)当坐标系变化时,即进行LPM和逆LPM时,由于需要某种形式的插值会导致水印图像质量急剧下降。
近年来很多人在探索基于不变矩的图像归一化技术来研究抗几何攻击的图像水印。在文[5]中提出了一种基于图像矩的图像归一化方法使水印信号能在一定程度上抗几何攻击。众所周知,图像归一化实际上是一种用于计算机视觉与模式识别的技术[6]。用此方法,水印信号的嵌入与提取都在一个有标准尺寸与方位的归一化图像中进行。这样,它就能适用于原始图像不可得的公共水印情况。但文[5]中这种方法的嵌入水印量非常小,只能嵌入1 bit水印,实际应用价值不高。
Masoud Alghoniemy等人在文[7]中把几何不变矩作为一个工具去解决几何不变问题,他们用了两种不同的方案来设计几何不变系统,即不变水印与图像归一化技术。对于不变水印来说,他们意思是指一个水印对几何攻击与一般信号处理攻击都是不变的。水印是基于不变参数从图像几何矩中提取的,他们也称其为不变矩。
Ping Dong等人在文[8]中也提出了一种用于抵抗几何攻击的水印方法。他们同样是用图像归一化技术解决水印抗仿射几何变换攻击问题,他们的方法与文[5]的不同之处在于,他们强调了更一般的仿射几何变换而不是仅仅局限于缩放和旋转变换攻击。
但是所有基于图像归一化技术的水印算法都面临着一个相同的问题,即嵌入水印后的图像必须经过一次逆归一化过程,在这个过程中,图像的质量会急剧下降。能否找到一种不用归一化技术而又能有效抗几何攻击的水印算法呢?这个问题看来只能在水印检测步骤寻求答案了。本文就针对此问题提出了一种不用归一化技术的水印检测算法,该算法是基于图心这一定义提出的,从仿射几何变换对图像图心的影响出发,我们提出了一种全新的应对几何攻击的水印检测算法。对大多数几何攻击后水印图像来说,应用我们的算法水印都能正常提取出来。由于我们的算法没有涉及水印嵌入步骤,所以对水印透明性没有产生任何影响。
本文其后部分组织如下:第二节我们提出了一种新的图像变换技术,称其为半下采样小波变换。我们在第三节提出了一种公共水印方案。在第四节中基于图心与仿射变换的关系提出了一种能有效抵抗各种形式仿射几何变换的水印检测算法。第五节用大量的实验来验证所提出的方法与算法的有效性。最后我们在第六节给出了本文的结论。
2 半下采样小波变换(SSWT)
为了去除小波变换中的吉布斯现象,M.J.Shensa[9]提出了非下采样小波变换。非下采样变换具有平移不变性,所以能有效去除变换中的吉布斯现象,这对图像水印技术是有益的,能有效提高水印的透明性。但非下采样变换的各子带大小相同,当水印信号嵌入到某个或某些子带经逆变换重构图像后,水印不能更好地得到扩散,这对水印的鲁棒性与透明性都是不利的。
基于以上讨论,本文发展了一种新的半下采样小波变换(SSWT)。首先对一幅图像进行非下采样金字塔(NSP)滤波,得到一个低频子带和一系列高频子带;对非下采样滤波后得到的低频子带进一步进行小波变换得到一个比原始图像小的低频子带和一系列高频子带,在此低频子带按水印嵌入算法嵌入水印后重构图像,水印就能在图像中更好地扩散,从而保证了水印的高透明性。
2.1 非下采样金字塔分解[10]
非下采样金字塔获得了一个平移不变的滤波结构,它是一种相似于拉普拉斯金字塔分解的子带分解方法,能通过两通道非下采样的二维滤波器组实现,图1说明了三级非下采样金字塔分解。这样分解后的结果只有J+1的冗余度,这里J表示分解级数,而三级小波变换分解后会有3J+1的冗余度。
在第j级理想的低通滤波通带支撑为[-(π/2j),(π/2j)]2,相应的理想的高通滤波通带支撑为低通滤波通带支撑的补,即[-(π/2j-1),(π/2j-1)]2[-(π/2j),(π/2j)]2。后序各级滤波器都通过上采样第一级滤波器获得,这样不需要另外的滤波器设计就可以得到多尺度分解。

图1 非下采样金字塔分解Fig.1 The pyramid decomposition fron non-lower sample
2.2 SSWT滤波器组构造
NSP变换能够将图像进行多尺度分解,同时具有平移不变性,平移不变性是图像分析中的一个很重要的性质。但由于在NSP变换中用上采样,使得变换后的各个子带都与原始图像大小相同,这并不利于在图像水印中的应用。为了提高水印的透明性与鲁棒性,我们需要一种子带尺寸递减的变换,让水印信号嵌入到较小的低频子带,使得水印信号经逆变换后在宿主图像中能够更加扩散,这有利于同时提高水印的透明性和鲁棒性。另外图像通过NSP变换后只滤掉了一部分强边缘,在水印嵌入低频子带之前有必要进一步滤掉部分弱边缘,这对提高水印的透明性与鲁棒性也是非常有利的。通过以上分析,我们设计了一种新的滤波方法,即先对图像进行NSP变换,再对得到的低频子带进行小波变换,我们称这种变换为半下采样小波变换(SSWT)。一幅图像经NSP分解后各子带大小相同,可以根据具体应用问题分别灵活选择NSP变换的级数和小波变换级数。由于小波滤波器组满足Bezout恒等式:

所以小波变换能完全重构;由文[10]可知,在一定条件下,NSP变换也能完全重构,从而本文提出的半下采样小波滤波器组能实现完全重构。图2给出了SSWT滤波器组设计方法。

图2 SSWT滤波器组Fig.2 SSWT filter set
3 基于SSWT的图像水印算法
为了说明SSWT的潜力,我们研究了它在图像水印中的应用,提出了一种新的水印算法:
(1)对宿主图像进行NSP变换,得到一个低频子带和一系列高频子带;
(2)对(1)中得到的低频子带执行小波变换,得到一个较小的低频子带和一系列高频子带;
(3)设计一个与(2)中得到的低频子带同样大小的水印,将水印按一定规则嵌入到低频子带;
(4)执行小波变换的逆变换;
(5)执行NSP变换的逆变换,得到嵌入水印后的图像。
3.1 水印嵌入
上述(2)中得到的低频带LLi是大小为N×N的系数矩阵,记为A,选择一个大小也为N×N的二值图像作为水印,记为B,在系数矩阵A中嵌入水印信息,即将两个N×N的矩阵进行信息迭加,其中含有水印信息的矩阵元素为0或1。下面是信息迭加的具体算法:

这里,T1,T2是水印嵌入的阈值,S是水印嵌入强度因子,在满足水印不可见的前提下尽量取大的值,T1,T2分别取3S/4和S/4。rem运算类似于mod运算,唯一的不同是,mod运算中的取整为向下取整,而rem运算中的取整为向零取整:

由Mallat算法可知,随着小波分解级数的增加,低频系数的幅值以近似2的倍数增长,而水印可看作在强背景下迭加一个弱信号(水印),只要迭加的信号低于对比度门限,视觉系统就无法感觉到信号的存在。而根据Weber定律,对比度门限和背景信号的幅值成比例,这就意味着,随着小波分解的级数的增加,嵌入水印的强度就可以近似2的倍数增加,从而使水印的鲁棒性增强。同时,小波分解的级数越大,水印分量可以更好地扩散,因此在水印算法中,应根据水印信息量多少,尽可能提高小波分解的级数。
3.2 水印提取
对嵌入水印后的图像执行第(1)、(2)步,得到小波变换后低频带LLi系数矩阵(记为Y),按如下公式即可检测出嵌入的水印信息:
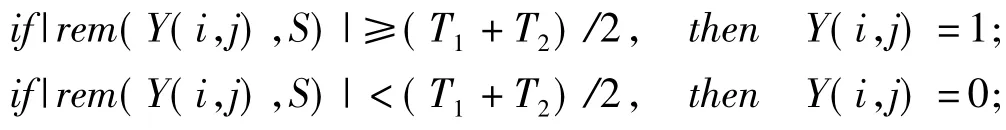
这样,水印信息就被恢复出来了。
对彩色图像我们只对其RGB三个通道中的任何一个作上述处理,就可以实现在彩色图像中嵌入水印,一般而言,将水印嵌入B通道,水印对一般信号处理攻击将会更鲁棒。
4 基于不变图心的水印检测
4.1 图心与仿射变换
Bum-Soo Kim等人在文[11]及Elijah Mwangi在文[12]中各自提出了基于不变图心的对几何攻击鲁棒的水印算法,他们的方法依旧没有摆脱图像归一化技术,仍然是先对图像进行归一化后再嵌入水印,所以得到的水印嵌入图像的质量仍然非常低。在本文中,我们只是把基于图心的方法应用于水印的提取步骤,所以能够得到高质量的水印嵌入图像.
令f(x,y)表示尺寸为 M ×N 的数字图像,它的几何矩 mpq,p,q=0,1,2,…被定义为(x,y).并且图心(x0,y0) 被定义为
一幅图像g(x,y)被称为另一幅图像f(x,y)的仿射变换,如果存在矩阵和向量d=使得 g(x,y)=f(xa,ya),这里:

显然旋转、缩放与平移变换都是仿射变换的特例,不失一般性,可以认为仿射变换不改变图像能量。
定理2 图像f(x,y)旋转一定角度再按同样角度反旋转后,图心不变。
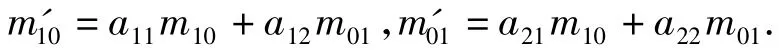
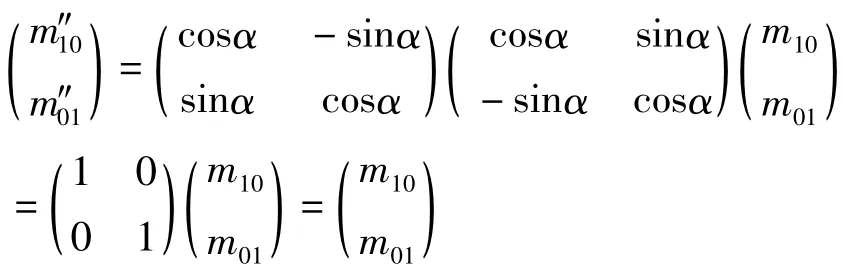

这里(x0,y0)为原始图像图心为旋转-反旋转后的图像图心。
定理3 图像f(x,y)缩放一定比例因子再按此比例因子的倒数反缩放后,图心不变;
所以:
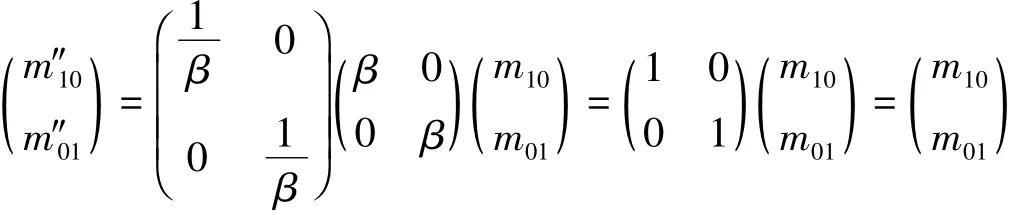

这里(x0,y0)为原始图像图心为缩放-反缩放后的图像图心。
由定理1可知,图像经过一定尺度平移后,图心也平移同样的尺度,但在平移后的图像上直接提取水印将会出问题,这是因为水印是嵌入到了经过N级小波分解后的低频子带,例如,经过三级分解后,低频子带的尺寸是原始图像尺寸的1/23,若原图平移1个像素,则小波低频子带的图心平移1/8个像素,也就是一个亚像素单位,破坏了水印信号的同步,因此水印不能正常提取。但是如果再把图像平移7个像素,这时三级分解后的低频子带的图心正好平移一个像素,这样就实现了水印信号的重同步,从而水印就能正常提取了。其实图像只要是平移8n(n∈Z)像素单位,水印就能重同步,水印信号也就能正常提取出来。
由定理2,图像经过旋转-反旋转后,图心不会发生改变,但在实际应用中,由于旋转过程要经过插值,所以反旋转后的图像会出现亚像素级的边框,所以无论怎样裁剪,都不能正好只把边框剪掉,实际情况如图3(b)所示,若直接对其提取水印就会失败。但是如果再重复一遍任一角度的旋转-反旋转后,问题就会迎刃而解,这时的亚像素边框就会恰好被剪掉,如图3(c)所示,从而实现能图心的归一化,并能完全正常提取水印。为了比较我们也给出原始图像的边框的一部分放大图,如图3(a)所示。实际应用中,只要是图像经过偶数次的旋转-反旋转变换,水印都能正常提取,这也说明了任一角度的旋转变换后水印信号用该方法都能实现重同步。

图3 旋转与反旋转后的图像亚像素边框比较,图中黄色区域为图像边界的放大图像.Fig.3 Comparison between rotary and anti-rotary image subpixel border,yellow area is the enlargedimage of image border
实际上,抗旋转攻击是最难解决的一个问题,现有文献中很多抗几何攻击的算法都是针对此问题提出的,由本文的理论分析和实验结果可知,本文对该问题的解决办法是即简单又有效。本文方法不仅适用于本文中所用的水印嵌入与提取算法,在其它算法中也同样适用,因为该问题的解决与水印的嵌入与提取算法本身没有任何关系。
由定理3,当图像经过任一比例的放大后再缩回,图心没有发生变化,从而能正常提取水印。但当图像先缩小再放大时,如果缩小程度过大,图像在缩小的过程中要经受低通滤波,再放大时要进行重采样与插值,从而使图心发生较大改变,这时提取水印质量就会有明显下降,由本文实验结果可知,当先缩小到原图的1/2后再放大回原图,水印还能正常提取,但若缩小比例再减小,提取的水印质量就会下降。
4.2 基于图心的水印重同步算法
在水印嵌入算法执行完以后,先计算出水印嵌入后图像的图心(x0,y0),后序检测算法都以此图心为标准。这里假设水印算法中小波分解为n级分解。
(1)如果图像遭受了平移攻击,计算图像图心得(xt,yt),与原图像图心(x0,y0)作差得:若a<2n或b<2n,则把图像继续平移2n-a或2n-b像素单位,然后就能正常提取水印信号了;若a>2n或b>2n,则把图像继续平移2n-mod(a,2n)或2n-mod(b,2n)个像素单位,再提取水印;若a=m·2n且 b=m·2n,m=0,1,2,3…则直接提取水印即可。
(2)对于缩放攻击由本文算法可知,在提取水印时无需作任何预处理,直接提取水印即可。
(3)对于旋转攻击,一般而言,可以通过图像是否有后加的边框,并且同时算出图像的图心,如果得到的结果与原始图像的图心有微小的差别,则认为图像可能遭受过旋转攻击,这时先进行一次水印提取算法,如果不能正常提取就给图像施加一次旋转-反旋转变换,这时水印就能正常提取了。
5 实验结果
在所有实验过程中,NSP变换都为二级变换,小波变换都为三级变换,小波变换所用的基为Haar小波基,所有插值运算全采用双三次插值。
5.1 灰度图像水印实验
对Lena(512×512)标准图像实验了上述算法。水印采用的是64×64的一幅“中国印”二值图像。图4为嵌入水印后的图像与提取的水印。为了说明本文提出算法的有效性,与传统的基于小波变换的水印算法进行了比较,我们分别用归一化相关系数(NC)与峰值信噪比(PSNR)来评价水印的鲁棒性与透明性。
通过计算PSNR来判断嵌入水印前后的两幅图像的差异来评价水印的透明性的高低,PSNR值越大,两幅图像差别越小,从而说明水印的透明程度越高。当两幅图像完全相同时,PSNR值为无穷大。通过计算NC值来定量地分析提取出的水印与原始水印的相似度,NC值越大两个水印越相似,当NC值为1时可认为两个水印完全相同。其中M1,M2为图像大小。
透明性:
为了与基于归一化技术的水印算法的透明性比较,本文首先对一幅没有嵌入水印的原始图像用文[8]中的归一化方法进行归一化与逆归一化操作,结果如图5所示。进行上述操作后,图像质量已经显著下降,PSNR值只为38.2110.当嵌入水印以后,图像的质量还会下降。
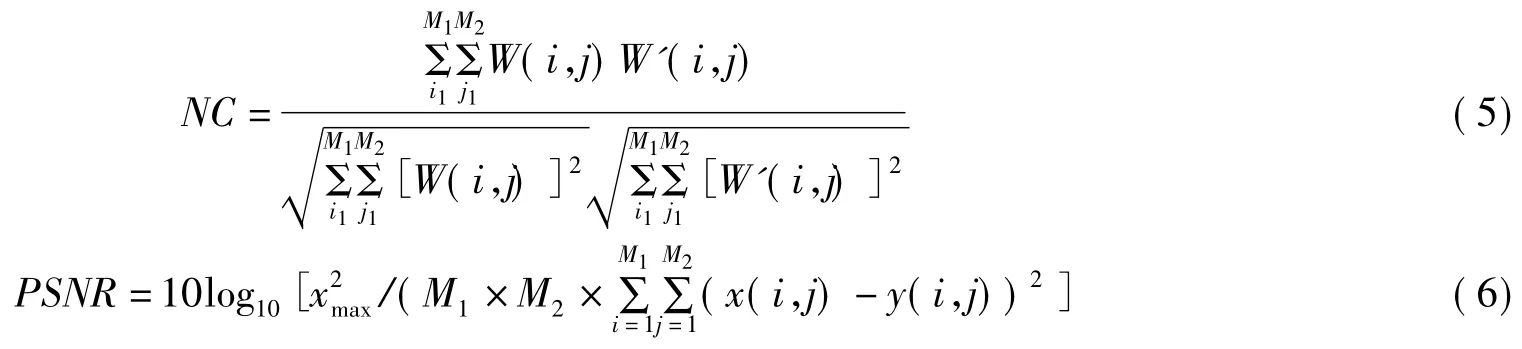
我们对原始图像进行二级NSP分解,然后对得到的低频子带进行三级小波分解,在得到的小波低频子带按水印嵌入算法嵌入水印,当嵌入强度因子S的取值为13.8时,提取的水印NC值刚好是1,而用基于小波变换算法当S的取值为16.1时NC值才能达到1。此时两种算法的PSNR值分别为52.2925与50.9738,随着S值的增大,PSNR值将变小,即嵌入水印后的图像质量降低。图6为SSWT算法与WT算法下的PSNR值比较。从图中可以看出当S取相同值时,基于SSWT算法的PSNR值一致高于WT算法的PSNR值,这说明本文算法中水印的透明性明显优于传统的基于小波变换的水印算法。


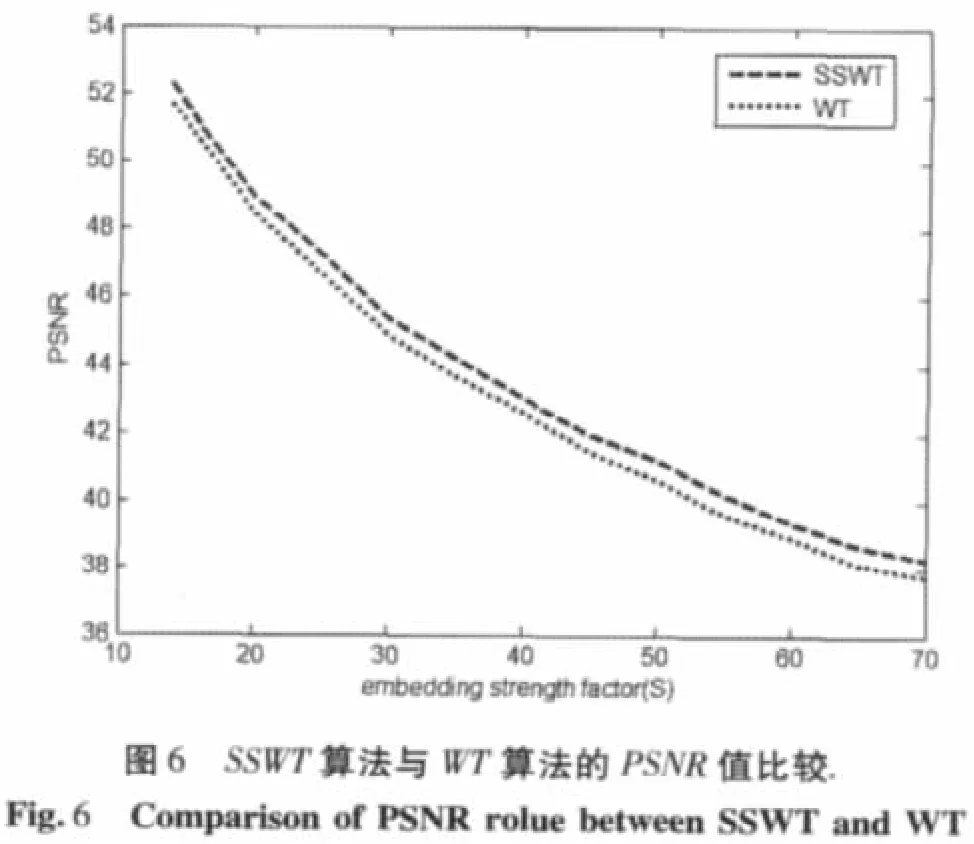
鲁棒性:
以下除没有说明以外,其余实验都是在S=13.8下执行的。
(1)平移攻击:我们首先把图像向下向右平移1个像单位后执行提取水印操作,然后再继续向下向右平移7个像素单位,即整体向下向右平移了8个像素单位后再提取水印,结果平移一个像素单位后提取失败,而再移8个像素单位后水印就能正常提取了。为了验证本文分析的正确性,我们还执行了其它的平移操作,所有结果如图7所示。

图7 水印图像平移及提取的水印.Fig.7 Translated watermark image and extracted watermark
(2)缩放攻击:我们对图像先进行一定比例的缩放然后反缩放再提取水印,图8为实验结果,从实验结果可以看出,本文方法在抗缩放攻击方面有很强的能力。

图8 水印抗缩放攻击结果.Fig.8 Theresult of watermark resistance to zoom attack
(3)旋转攻击:我们对各个角度的旋转攻击按我们的方法进行了实验,实验中第二次旋转的角度分别为45°与 -45°,但实际上第二次旋转可以选任意角度。实验所用的嵌入强度因子为 S=13.8,但提取的水印除了有小的边框处,真正的有意义水印部分已经相当清晰,如果再调大嵌入强度因子,实验结果将会更加理想。实验结果表明本文所提出的方法非常简便但相当有效。实验结果如表1所示。在表1中我们看到,只有当旋转角度为20°时,提取水印的有意义部分有些噪声,其余所有提取的水印效果都比较理想。
(4)联合攻击(图像归一化攻击)
由文[8]的图像归一化算法可知,图像在归一化过程中要依次经过平移、剪切、缩放及旋转等几何变换,在本部分实验中我们就应用文[8]中算法对水印嵌入图像进行一次图像归一化,然后逆归一化再提取水印,从而实现了各种形式的几何攻击的联合攻击。实验结果如表2所示。从实验结果可以看出,本文算法在抵抗各种形式几何攻击的联合攻击下,同样有良好的性能。


(5)SSWT与WT对比实验
下面我们对两种算法分别进行了大量的对比实验来测试本文算法的水印鲁棒性,通过对两种算法得到的水印图像进行多种形式的攻击,包括添加高斯噪声,中值滤波,以及缩放与旋转几何攻击。
本部分实验中,SSWT算法的 PSNR=47.5360(S=24),WT算法的 PSNR=46.6110(S=24)。
图9为两种算法中水印分别对抗高斯噪声添加与椒盐噪声添加性能比较,从图中可以看出,本文算法在添加高斯噪声情况下的鲁棒性较基于WT算法的鲁棒性有了显著的增强,对椒盐噪声添加,本文算法也有明显的优势。表3为两种算法抗缩放和旋转几何攻击性能比较,在实际实验中计算NC值时没有考虑提取出的水印的边框信息。通过对表3中两种算法的NC值的比较可以看出,本文算法在对抗这两种几何攻击方面也明显优于基于WT的算法,特别是对抗旋转攻击,无论图像进行多少度的旋转,本文算法的NC值都为1,这说明了本文算法在对抗几何攻击方面有着无可比拟的优势。表4为中值滤波情况下两种算法水印鲁棒性的比较,从表中NC值的比较可以看出,本文算法在中值滤波情况下优势明显。总之,本文算法对实验中所用的各种形式的攻击的鲁棒性都在某种程度上优于基于WT的算法。

表3 水印抗几何(旋转与缩放)攻击的鲁棒性比较.Table.3 Robustness comparison of waterwark resistance to rotation and zoom attack

图9 水印抗高斯噪声和椒盐噪声比较.Fig.9 Comparison of watermark from anti-gaussian and salt-pepper noise

表4 水印对中值滤波的鲁棒性比较.Table 4 Robustness comparison of watermark to median filter
5.2 彩色图像水印实验
本部分对一幅彩色Lena(512×512)图像进行水印实验,原始图像与嵌入水印后的图像及提取的水印如图10所示。只给出平移攻击与旋转攻击的实验结果,平移攻击结果如图11所示,旋转攻击结果如表5所示。其余实验结果与灰度图像相似,这里不再重述。水印按本文提出的算法嵌入到B通道中,PSNR值按彩色图像PSNR值计算公式计算。



图11 水印图像平移及提取的水印。Fig.11 Translated watermark and extraeted watermark
6 结论
本文通过提出的半下采样小波变换的变换域的低频子带嵌入水印,提高了水印的高透明性。由于在嵌入过程中没有采用图像归一化技术,所以保证了水印嵌入图像的高质量。我们针对水印对几何攻击的鲁棒性,基于图心与仿射变换的关系提出了一种水印信号重同步的方法,用该方法能有效抵抗各种形式的仿射变换几何攻击。文中分别对灰度图像与彩色图像做了大量的实验来验证本文所提出的方法与算法的有效性,从实验结果可知,我们提出的方法虽然简便但取得了理想的效果。由于本文所提出的抵抗几何攻击的水印检测算法与本文所用的水印嵌入算法与提取算法并没有直接的关系,所以该算法具有一定的通用性,用于其它类似的水印嵌入与提取算法,相信也会取得理想的效果。
[1] 金 聪,叶俊民,许凯华,等.具有抗几何攻击能力的盲数字图像水印算法[J].计算机学报,2007,30(3):474-482
[2] 王 丹,陆佩忠.一种可抵抗局部几何攻击的多比特水印算法.南京理工大学学报(自然科学版)[J],2008,32(4):406-410
[3] 袁大洋,肖 俊,王 颖.数字图像水印算法抗几何攻击鲁棒性研究[J].电子与信息学报,2008,30(5):1251-1256
[4] O’Ruanaidh J J K,Pun T.Rotation,scale and translation invariant spread spectrum digital image watermarking[C].Signal processing,1998,66(3):303-317
[5] M.Alghoniemy ,A.H.Tewfik.Geometric distortion correction through image normalization[C].Presented at the ICME Multimedia Expo,2000
[6] J.Wood.Invariant pattern recognition:A review[J].Pattern Recognition.1996,29(1):117
[7] Masoud Alghoniemy ,Ahmed H.Tewfik.Geometric Invariance in Image Watermarking[J].IEEE Trans.on Image Processing,2004,13(2):145-153
[8] Ping Dong,Jovan G.Brankov,Nikolas P.Galatsanos,Yongyi Yang,and Franck Davoine.Digital Watermarking Robust to Geometric Distortions[J].IEEE Trans.on Image Processing,2005,14(12):2140-2150
[9] M.J.Shensa.The discrete wavelet transform:Wedding the à trous and Mallat algorithms[J].IEEE Trans.S ignal Processing,1992,44(10):2464–2482.
[10] A.L.Cunha,Jianping Zhou,Minh N.Do.The Nonsubsampled Contourlet Transform:Theory,Design,and Applications[J].IEEE Trans.on Image Processing,2006,15(10):3089-3101
[11] Bum-Soo Kim,Jae-Gark Choi,Kil-Houm Park.Image Normalization Using Invariant Centroid for RST Invariant Digital Image Watermarking[C].Lecture Notes in computer Science,Volume 2613/2003,201-210
[12] Elijah Mwangi.A Geometric Attack Resistant Image Watermarking Scheme Based on Invariant Centroids[C].2007 IEEE International Symposium on Signal Processing and Information Technology.190-193

