基于阿基米德联合函数的洪水过程随机模拟研究

杨立峰，周研来，夏世明，曾令军

（1.中国水利水电第十四工程局有限公司，云南 昆明 650041；2.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072）

洪水过程的随机性是复杂水文系统中较难描述的不确定性因素之一。洪水过程随机模拟国内外已有多种模型[1-3]。近年来，非参数方法[3]、小波分析理论[4]以及联合 （Copula）函数[5-8]等被先后应用到洪水随机模拟领域，极大地丰富了洪水随机模拟的理论和方法。文献 [7]采用耿贝尔联合 （Gumbel-Hougard Copula）函数对洪峰和洪量建立联合随机模型，初步探讨了Copula函数在洪水过程随机模拟中的应用。文献 [8]应用Gumbel-Hougard Copula函数构造洪峰与历时的联合分布，以及相邻截口的联合分布，较好地描述了洪峰、历时的统计特征及相关关系，但洪量的统计特征值的模拟精度相对较差。

本文分别采用三种阿基米德联合 （Archimedean Copula）函数对洪峰和洪量建立联合随机模型，从实测资料中优选峰量比接近的洪水过程进行缩放得到模拟的洪水过程线，来探讨阿基米德联合函数在洪水过程随机模拟中的适用性。实例表明：Copula模拟模型弥补了常规模型模拟峰和量的统计特征不能同时与实测系列保持一致以及生成洪水的频率分布偏离洪水设计值的理论频率分布较大的不足，其模拟系列能够很好地保持实测洪水过程线的形状，截口具有随机波动性、无锯齿现象。

1 洪水过程的随机模拟模型

1.1 Copula理论

Sklar在1959年提出了著名的多元分布的Sklar定理[10]：

令 F（·，…，·）为具有边缘分布 F1（·），F2（·），…，FN（·）的联合分布函数，那么存在一个Copula函数C（·，…，·）， 满足

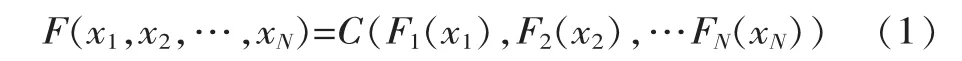
若 F1（·），F2（·），…，FN（·）连续， 则 C（·，…，·）唯一确定； 反之， 若 F1（·），F2（·），…，FN（·）为一元分布，C（·，…，·）为相应的Copula函数，那么由式（2） 定义的函数 F（·，…，·）为具有边缘分布 F1（·），F2（·），…，FN（·）的联合分布函数。 Gumbel-Hougard、克莱特 （Clayton）和弗兰克 （Frank）联合函数是三种常用于随机模拟领域的单参数Archimedean Copula[6，10]。

N元Gumbel-Hougard Copula函数

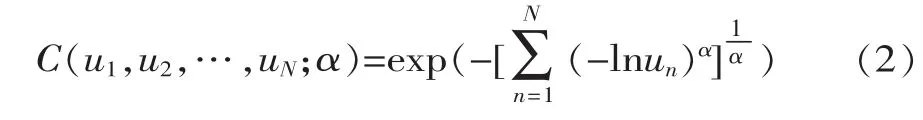
式中， un=Fn（xn），n=1，2，…， N 为边缘分布函数， α∈[1，∞）为Gumbel-Hougard Copula函数的参数。该函数仅能够适用于变量存在正相关的情形，因此，较适用于构造如洪峰和洪量、洪量与洪水历时等变量之间存在的正相关的联合分布。

N元Clayton Copula函数

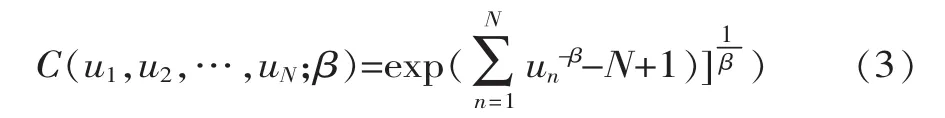
式中，β∈（0，∞）为Clayton Copula函数的参数。该函数与Gumbel-Hougard Copula函数一样，均仅适合描述正相关的随机变量。

N元Frank Copula函数

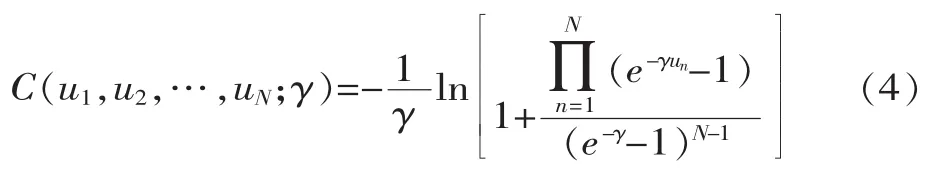
式中， γ∈（-∞，+∞）{0} 为 Frank Copula函数的参数。该函数既能够描述正相关的随机变量，也能够描述存在负相关的随机变量。

通过Sklar定理，可以将一个N维的联合分布函数分解为N个边缘分布和一个Copula函数，这个Copula函数描述了变量间的相关性 [5，6，10]。 因此， 中参数 C（u1，u2，…，uN；θ）的估计成为了一个非常重要的问题。国内外许多学者对此问题做了广泛的研究[5，6，9，10]， 主要有非参数估计方法和参数估计方法。非参数估计法包括Kendall秩法、Spearman秩法等。非参数估计法适用于单参数的两变量阿基米德联合函数估计。参数估计法主要有极大似然估计法 （ML）、 两步法 （IFM）、 半参数法 （CML）， 其中ML与IFM作参数估计时，必须对边缘分布作出假设和检验，才能估计出Copula函数中的参数，而CML不需对边缘分布作出假设[8]。

1.2 Copula联结模型

本次研究采用阿基米德联合函数来描述洪峰和洪量的相关性结构，在此仅以Clayton Copula函数为例来表述洪峰和洪量的相关性。即

式中，β∈（0，∞）为Clayton Copula函数的参数，β越大，相关性越强；当β趋近于0时，变量相互独立。

根据洪峰Qm和时段洪量W的边缘分布FQm（qm）和 FW（w）以及 Copula函数 （式 （5））， 由 Sklar定理（式 （1））， 可以得到联合分布 F（qm，w）

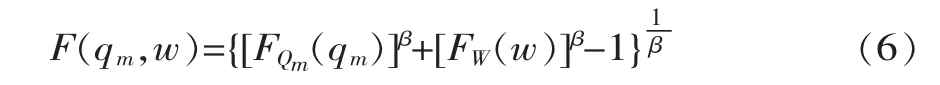
式中， FQm（qm）， FW（w）均为 P-III型分布。

联合分布的参数估计先用Kendall秩法初估计，然后用两步法 （IFM）校正。单参数的两变量Clayton Copula函数的参数β与Kendall秩τ存在确定的解析关系[5，6，9，10]

两步法校正参数：第1步，根据Qm和W的观测值系列，采用单变量的参数估计边缘分布FQm（qm）和FW（w）的参数；第2步，估计Copula函数的参数β。最优的估计值β应使得

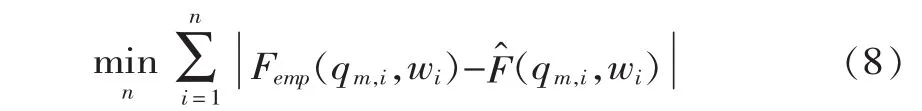
式中， Femp（qm，i，wi）为根据联合观测值 （qm，i，wi）求出的经验联合分布[5，6]， F＾（qm，i，wi）为所采用的理论分布的估计值。

一般按照峰高量大，主峰靠后的年最大值法选出的洪水样本，其洪峰和洪量都具有一定的相关性[7]。采用峰量联合分布对洪峰和洪量进行联合描述，通过联合分布的随机抽样方法可以对存在相关性的峰和量成对取样，从而达到随机模拟洪峰和洪量的目的。峰量随机抽样方法以及模拟洪水过程线的方法，具体步骤详见文献[7]。

2 实例研究

黄河中上游某水库的流域控制面积为8 847 km2，有20年实测坝址洪水资料 （1959年至1978年，每年7月1日到10月31日，次洪历时大多为24 h）。在实测洪水资料中，按照 “峰高量大、主峰靠后”的原则每年选择一场历时为34 h的最大洪水过程，构成样本容量为20的34 h（截口间距为20 min）洪水过程系列。从每一年洪水过程中， 取样得到一对洪峰Qm和1日洪量W1d，构成20个Qm和W1d的联合观测值系列，并据此建立Qm和W1d的两变量联合分布。Qm和W1d的边缘分布采用P-III型分布，分别为 FQm（qm）和 FW1d（w1d）。 洪峰和洪量边缘分布函数的拟合分别见图1和图2。

图1 洪峰边缘分布函数的拟合曲线

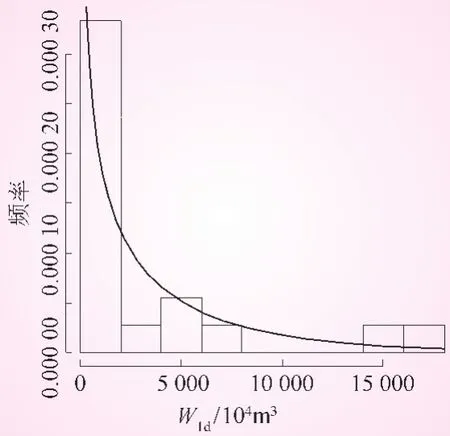
图2 洪量边缘分布函数的拟合曲线

采用矩法估计洪峰和洪量实测系列的统计特征值 （见表1），并假定估计的参数为该水库区间洪水洪峰和洪量总体分布的参数。对Qm和W1d的联合观测值计算Kendall秩τ等于0.7516，据Kendall秩与Gumbel-Hougard、Clayton和Frank Copula函数的解析关系式[10]初估Copula函数的参数分别为α=4.02、β=6.04及γ=14.24。为进一步校核Copula函数的参数，点绘20年的Qm和W1d的经验联合分布值与理论联合分布值 （在此仅以Clayton Copula模型为例）拟合最佳的曲线如图3所示。将调整后的参数α、β及γ作为Copula函数的估计值。据式 （2）～（4），可以得到 Qm和W1d的 Gumbel-Hougard、Clayton和Frank联合分布函数分别为

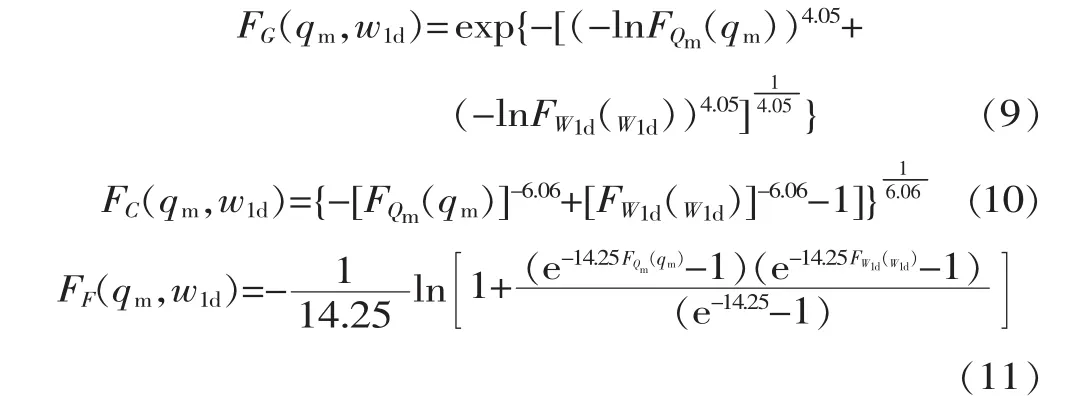
依据峰量随机抽样方法以及模拟洪水过程线的方法，可随机模拟出M （如10万）条洪水过程线，用矩法估计模拟系列的统计特征值见表1。

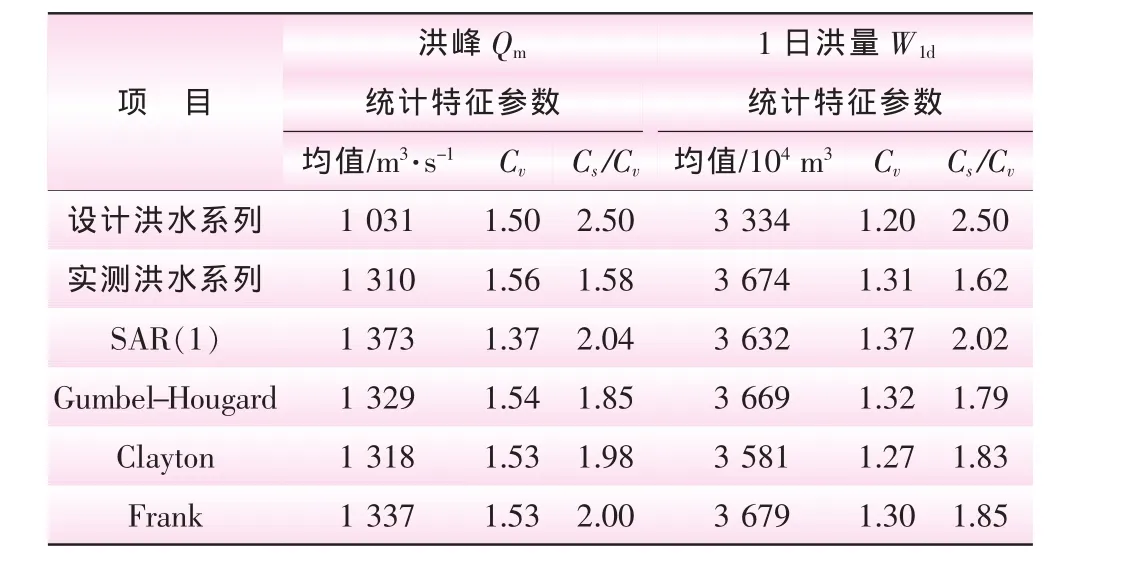
表1 实测系列和模拟系列洪峰和洪量的统计特征值

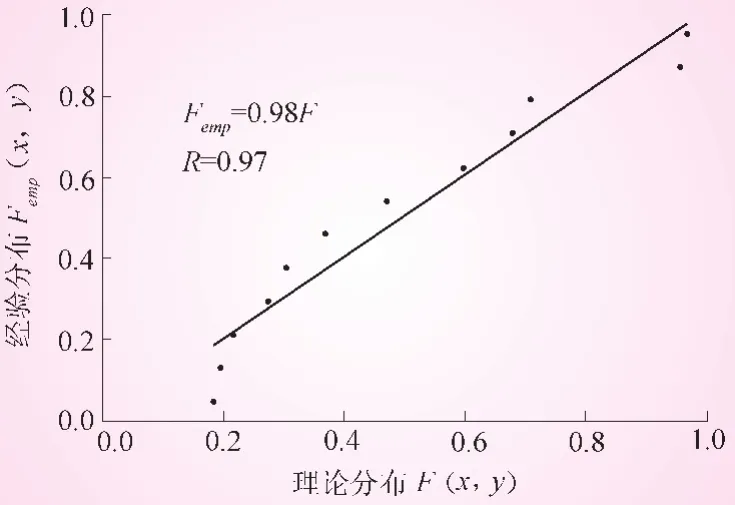
图3 基于Clayton Copula的联合观测点的经验分布和理论分布的相关关系

由随机抽样得到洪峰和洪量值，可求得对应的峰量比值，并依据该比值优选峰量比值最接近的实测洪水过程，采用变倍比方法进行缩放，图4给出了以1961年实测洪水过程为例进行缩放得到的若干洪水过程线 （在此仅以Gumbel-Hougard Copula模型为例），图5给出了SAR（1）季节性阶自回归模型模拟的若干洪水过程线。

模拟生成的洪水频率分布是否接近理论频率分布是评价随机模型的适用性重要指标之一。由上述4个随机模型模拟生成10个样本容量为10万的洪水过程，结合综合判别法来分析洪水的量级 （用重现期表示），即在洪水调度中按库水位和入库流量中哪一项先满足各自的最大值来判别洪水的级别，便可计算出10个模拟样本的大于不同重现期设计值的平均频次 （四舍五入取整）见表2。

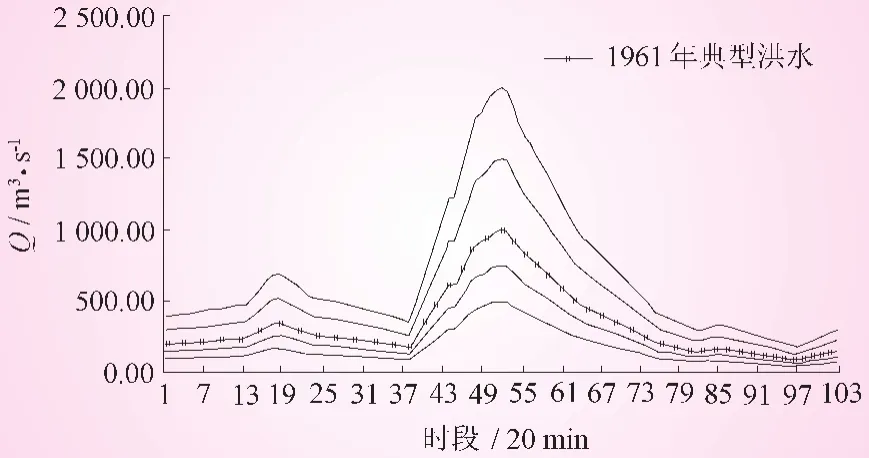
图4 以1961年实测洪水过程为例进行缩放得到的若干洪水过程线

图5 SAR （1）模型模拟的若干洪水过程线

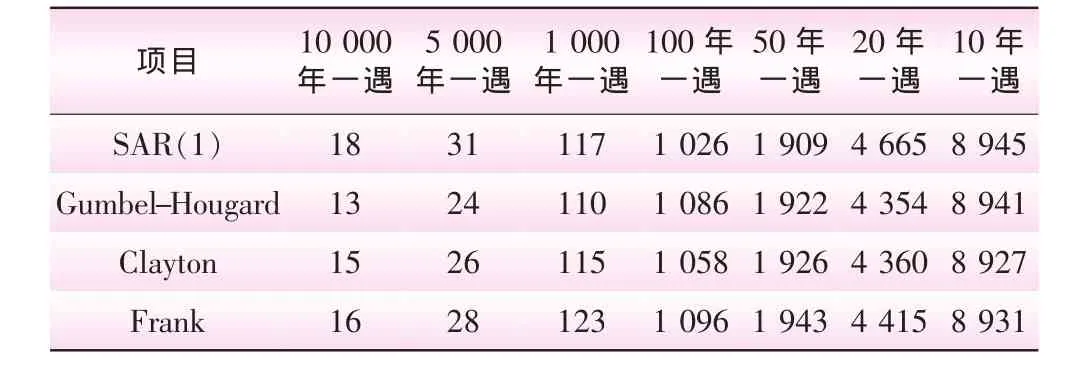
表2 大于不同重现期设计值的频次 （基数10万次）

3 方法的比较分析

本文以SAR（1）模型为参照，从洪水统计特征参数、洪水过程线及洪水频率分布三个方面来评价Copula模型的在洪水过程随机模拟领域的适用性。

由表1和图3可知，三种Copula模型虽然在洪峰和洪量的统计特征指标上存在差异，但是均能保持实测洪水系列的统计特征，且三种模拟模型在峰和量的统计特征上均优于SAR（1）模拟模型。

由图4和图5可知，SAR（1）模拟的洪水过程线型具有多样性和各个截口有较好随机波动性，但存在明显的锯齿现象；而Copula模拟的洪水过程线型不但保持了实测洪水过程线型，而且无锯齿现象。

由表2可以看出，四种模拟生成的100年一遇至10 000年一遇的大洪水平均频率分布上均高于理论频率分布，小洪水平均频率分布上均略低于洪水设计值的理论频率分布，但Copula模型的洪水平均频率分布较SAR（1）模型更接近洪水设计值的理论频率分布。

4 结论

本文构建了洪峰和洪量的联合分布，分别采用了三种Archimedean联合分布随机抽样方法模拟了洪水过程线，以SAR（1）模型为参照，探讨了Archimedean Copula函数在洪水过程随机模拟领域的适用性。虽然三种Archimedean Copula模型生成的洪水过程的洪峰和洪量统计特征有细微的差别，但均具有保持实测系列洪峰和洪量统计特征的优点，且能够反映实测洪水过程的形状及洪水频率分布特征。该模型也存在不足，如无法模拟洪峰与历时的相关特性，且洪峰和洪量的时程分配形式受实测资料长度的限制。

［1］ 梅亚东，谈广鸣.大坝防洪安全的风险分析［J］.武汉大学学报（工学版）， 2002， 35（6）:11-15.

［2］ 丁晶，邓育仁，侯玉，等.水库防洪安全设计时设计洪水过程线适用性的探讨［J］.水科学进展， 1992， 3（1）:46-52.

［3］ 袁鹏，王文圣，丁晶.洪水随机模拟的非参数扰动最近邻自展模型［J］.四川大学学报 （工程科学版）， 2000， 32（1）:82-86.

［4］ 王文圣，袁鹏，丁晶.小波分析及其在日流量过程随机模拟中的应用［J］.水利学报， 2000， 31（11）:43-48.

［5］ 熊立华，郭生练，肖义，等.Copula联结函数在多变量水文频率分析中的应用［J］.武汉大学学报 （工学版）， 2005， 38（6）:16-19.

［6］ 郭生练，闫宝伟，方彬，等.Copula函数在多变量水文分析计算中的应用及研究进展［J］.水文， 2008， 28（3）:1-7.

［7］ 肖义，郭生练，熊立华，等.一种新的洪水过程随机模拟方法研究［J］.四川大学学报 （工程科学版）， 2007， 39（2）:55-60.

［8］ 张涛，赵春伟，雒文生.基于Copula函数的洪水过程随机模拟［J］.武汉大学学报 （工学版）， 2008， 41（4）:1-4.

［9］ 闫宝伟，郭生练，刘攀，等.基于Copula函数的径流随机模拟［J］.四川大学学报 （工程科学版）， 2010， 42（1）:5-9.