剖分变径带式无级变速器传动比波动分析

肖义成，付风岚，周孙彪

(1．湖北省机电研究设计院行业服务中心，湖北 武汉 430070;2．武汉理工大学机电工程学院，湖北 武汉 430070)

带式无级变速器是一种结构简单、使用广泛的机械式无级调速装置［1－3］，常规的V带无级变速器是通过移动可动锥盘，挤压V带，调节带槽宽度调节带轮的工作直径改变传动比，利用带的张紧力使带与带轮之间产生摩擦来传递动力。然而，这种带与带轮之间剧烈摩擦的调速方式，直接造成带的较快磨损，降低其使用寿命［4－6］。为了克服这一缺陷，近年来出现了一种通过直接改变带轮直径进行无级调速的剖分变径带式无级变速器［7－8］。目前，大连交通大学、武汉科技大学等单位开展了对这种新型无级变速器的研究工作，初步掌握了其设计方法，但还有很多问题有待深入研究。如该无级变速器在调速过程中存在带长变化的问题，由此会引起传动比的波动和传动带张紧力的变化，笔者将对该问题进行详细的探讨。

1 剖分变径带式无级变速器工作原理

剖分变径带式无级变速器有多种结构，典型特征是带轮不是整体式的，而是由多个径向剖分的带轮块组合而成。图1是无级变速器的一种结构方案，它由剖分式主、从动轮，传动带，张紧弹簧，变速杠杆等组成［9］。主、从动轮均由剖分带轮块、径向导向盘、滑动锥盘组成，主、从动导向锥盘分别固定在输入轴和输出轴上，主、从动滑动锥盘用花键分别安装在输入轴和输出轴上并可沿轴向滑动，剖分带轮块与径向导向盘和滑动锥盘用T型槽构成滑动联接。传动带用两张紧弹簧紧套在主、从动轮上，两张紧弹簧分别安装在主、从动轮的滑动锥盘与滑动套筒之间，两滑动套筒分别空套在输入轴和输出轴上，滑动套筒的尾部有环型槽，变速杠杆的两端分别插入两滑动套筒尾部的环型槽中。

图1 剖分变径带式无级变速器结构原理

直流电机通过蜗轮蜗杆驱动变速杠杆。当变速杠杆从垂直位置开始顺时针方向摆动时，主动轮的剖分带轮块向内移动，带轮工作直径变小;同时，从动轮的剖分带轮块向外移动，带轮工作直径变大，从而连续改变传动比，实现减速传动。反之，当变速杠杆逆时针方向摆动时，可连续调节超速传动比。

2 传动带长度的变化

从剖分变径带式无级变速器的工作原理可以看出，两带轮的中心距是一定的，当带轮的工作半径发生变化时，理论带长也会随之发生变化。理论带长的计算公式［10］为:

式中:a为中心距;R1、R2分别为主、从动带轮的工作半径;i为传动比。

由于传动比的变化是由变速杠杆控制的，在调速过程中，主、从动带轮工作半径的变化量受变速杠杆的杠杆比影响。在主、从动轮滑动锥盘锥角相同的情况下，杠杆比与主、从动带轮工作半径的变化量之间的关系可表示为:

式中:a、b分别为变速杠杆转动中心到输入、输出轴的距离;ΔR1、ΔR2分别为主、从动带轮工作半径的变化量;k为杠杆比。

以传动比i=1时变速器的状态为基准，此时变速杠杆处于垂直位置。设基准状态下，R1=R2=R0。当变速器减速传动时，传动比为:

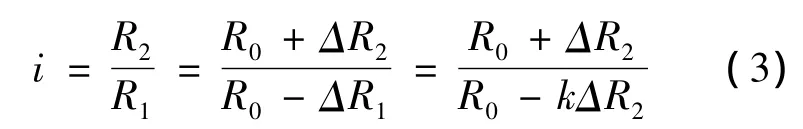
由式(3)可以得到:

用 R1=R0－ΔR1，R2=R0+ΔR2代入式(1)并结合式(4)，可有:

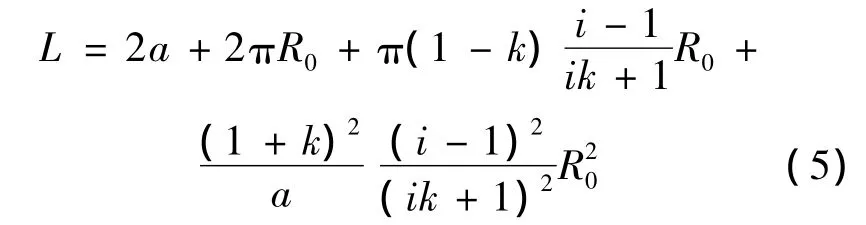
在式(5)中，第1和第2项为基准带长L0，是设计变速器时确定的实际带长;第3和第4项为某一传动比(减速传动)下带长相对于基准带长的变化量ΔL。

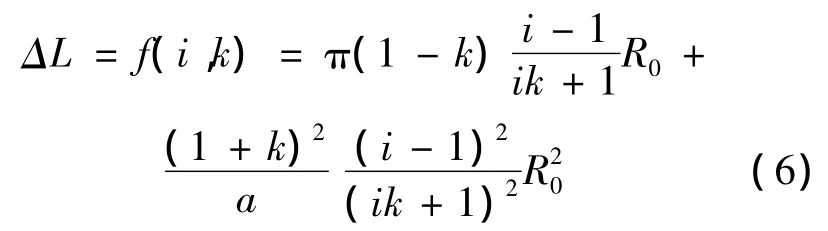
当超速传动时，带长变化量计算式(6)仍然适用，但式(6)中的传动比要用1/i，杠杆比要用1/k代入。

从式(6)可以看出，带长的变化是传动比和杠杆比的非线性函数，希望带长的变化越小越好，这显然是一个函数的极值问题。

3 传动比的波动

无级变速器在传动过程中，理论带长会随传动比的改变发生变化，而实际带长(即基准带长)是不变的。当传动带理论带长发生变化时，在张紧弹簧的作用下，带轮直径会发生少许变化，以保证理论带长和实际带长相等。因此，传动比会发生波动，并影响到传动带张紧弹簧张紧力的变化。

当实现某一传动比时，带长的变化量可由张紧弹簧的变形来补偿。此时，张紧弹簧的补偿变形会有主动轮张紧弹簧补偿变形、从动轮张紧弹簧补偿变形和主、从动轮张紧弹簧同时补偿变形3种情况，笔者针对减速传动工况分别进行讨论。

(1)主动轮张紧弹簧补偿变形。设主动轮张紧弹簧补偿变形量为Δx1，相应的主动轮半径的补偿变化量为δR1，由式(1)可以导出:

由式(7)可以求出主动轮半径的补偿变化量δR1。由于主动轮半径发生了变化，传动比也随之改变，实际传动比此时，主动轮张紧弹簧补偿变形量Δx1=δR1tan α，式中，α为滑动锥盘的锥角。

(2)从动轮张紧弹簧补偿变形。设从动轮张紧弹簧补偿变形量为Δx2，相应的从动轮半径的补偿变化量为δR2，同上，由式(1)可以导出:

由式(8)可以求出从动轮半径的补偿变化量δR2。由于从动轮半径发生了变化，传动比也随之改变，此时的实际传动比，从动轮张紧弹簧补偿变形量 Δx2=δR2tan α。

(3)主、从动轮张紧弹簧同时补偿变形。当主、从动轮张紧弹簧同时变形来补偿带长变化时，其补偿变形量介于上述两种情况之间。

当超速传动时，计算主、从动轮半径的补偿变化量的式(7)和式(8)仍然适用，但对主、从动轮的定义要互换。

4 实例分析

已知带轮的基准工作半径R0=70 mm，中心距a=210 mm，传动比的变化范围 i=0．80～2．45。减速传动时不同传动比下的最优杠杆比如图2所示，对应的带长变化量如图3所示。在整个调速范围内使带长变化相对较小的最佳杠杆比k=1．16，对应的带长变化如图4所示。从图4可以看出，在超速传动区间，理论带长变长，带长的变化随传动比增大而减小;在减速传动区间，随着传动比的增大，理论带长是先变短后变长，带长的最大变化量如表1所示，与最大带长变化量对应的传动比的波动如表2所示。

图2 最优杠杆比

图3 最优杠杆比下的带长变化量

图4 杠杆比为1．16时的带长变化量

表1 带长的最大变化量

表2 传动比的波动

从表2中可以看出，传动比的波动比较小，最大相对波动量为2．5%，能满足一般传动系统的要求，张紧弹簧的最大补偿变形量仅为1．08 mm，只要合理选择张紧弹簧的刚度，完全可以保证传动带有足够的张紧力。值得注意的是，当理论带长变长时传动带的张紧力会增大，有利于变速器的传动。

5 结论

剖分变径带式无级变速器在调速过程中存在带长变化的问题，由此会引起传动比的波动和传动带张紧力的变化。实例分析表明，对机械剖分变径带式无级变速器，只要变速杠杆的杠杆比选择恰当，可以将传动比的波动和传动带张紧力的变化控制在很小的范围内，完全能满足一般传动系统的要求。笔者的研究结论对剖分变径带式无级变速器的设计具有指导作用。

［1］ 冯樱，罗永革，何小春，等．CVT无级变速器的发展综述［J］．湖北汽车工业学院学报，1999，13(4):10－14．

［2］ 石启军．汽车无级变速器简介［J］．中国科技信息，2009(7):117－118．

［3］ 王幼民，唐铃凤．金属带式无级变速器的研究综述［J］．机械传动，2007，31(6):95 －99．

［4］ 郭翼超，何维廉，黄宏成．金属带式CVT的钢带轴向偏移分析［J］．传动技术，2001(4):43－47．

［5］ 杨亚联，秦大同，王红岩，等．CVT无级变速传动钢带轴向偏移分析［J］．重庆大学学报:自然科学版，1999，22(6):1 －7．

［6］ 郝石磊．新型CVT无级变速器动力传递机构的设计［J］．湖北汽车工业学院学报，2007，21(4):78 －80．

［7］ 邵万珍，葛宰林，崔永．一种新型径向V带无级变速器［J］．机械传动，2005(5):82－84．

［8］ 马忠驰，张光德，刘旺，等．剖分变径式无级变速器原理设计与分析［J］．上海汽车，2009(6):20－22．

［9］ 赵倩．剖分变径带轮CVT的动力性能仿真研究［D］．武汉:武汉科技大学图书馆，2010．

［10］ 普明．带传动理论与新型带传动［M］．北京:国防工业出版社，2006:52－66．